Конспект уроку з алгебри для 8 класу по темі " Квадратні корені"

Урок з алгебри для 8 класу

Тема: узагальнення знань по темі «Квадратні корені».

Мета: 1. Через гру узагальнити та систематизувати знання про квадратні корені, здобуті на попередніх уроках; продовжувати формувати в учнів уміння та навички перетворювати вирази, що містять квадратні корені.

2. Розвивати логічне мислення, пам’ять, увагу, обчислювальні навички учнів.

3. Виховувати культуру математичних записів та мови; інтерес до предмету, наполегливість і старанність у праці, чесність, почуття товаристкості та доброзичливості.

Тип уроку: урок-змагання.

Обладнання уроку: проектор; таблиця з «магічним» квадратом; амулет «магічний» квадрат; таблиця з многокутником для «поля чудес»; сигнальні картки (червоні та сині) для оцінювання; картки для усного рахунку; індивідуальні картки; вислови Р.Декарта та Б.Паскаля про математику.

Хід уроку:

Біля дошки, як епіграф уроку, висять вислови:

1) «Предмет математики такий серйозний, що корисно не нехтувати нагодою робити його трохи цікавішим».

Б.Паскаль

2) «Недостатньо лише мати добрий розум, головне – це раціонально застосовувати його».

Р.Декарт

1. Організаційна частина (вступне слово вчителя).

Сьогодні у нас заключний урок по темі «Квадратні корені». Підводячи підсумок вивченого, ми повторимо основні факти по даній темі – означення квадратного кореня, його властивості, попрацюємо над перетворенням виразів, що містять квадратні корені, а результати засвоєння даної теми ми з’ясуємо на наступному уроці – в процесі написання тематичної контрольної роботи.

Даний урок ми проведемо у нестандартній, але відомій вам формі – у формі змагання між чарівною та сильною половинами класу.

Для підведення підсумків результатів змагання нам потрібно журі. Сьогодні до складу журі будуть входити: (представлення журі).

Під час роботи на уроці прохання дотримуватись тиші, в кожній відповіді буде враховано правильність, точність, повнота і, оскільки це змагання, швидкість.

На партах у вас знаходяться червоні та сині картки, за кожну абсолютно правильну відповідь ви чесно відкладаєте в свій бік червону картку, за неточну – синю. В кінці уроку тих учнів, яких неможливо буде оцінити зразу (неповні відповіді, відповіді-доповнення), буде оцінено за наявністю та кількістю червоних і синіх карток.

На сьогоднішньому уроці члени журі, якщо це буде можливо, виділять переможців у таких номінаціях: Міс або Містер Точність, Міс або Містер Активність, Міс або Містер Ввічливість.

Переможці в даних номінаціях отримають додаткові бали з алгебри по темі «Квадратні корені».

2. Проведення змагання.

І конкурс «Розминка»

Оцінювання: правильна відповідь команди з першого разу – 2 б., з другого або виправлення – 1 б., відповідь іншої команди – їй 1 б.

1. Сформулювати означення квадратного кореня з числа а. Навести приклади.

2. Сформулювати означення арифметичного квадратного кореня з числа а. Навести приклади.

3. Коли дана рівність буде правильною? Прочитати її. .

4. Коли вираз не має змісту? Чому?

5. Сформулювати властивості арифметичного квадратного кореня.

а)                            в)

б)                                    г)

6. Чи має рівняння корені? Скільки?

7. Які числа називаються раціональними?

8. Якою властивістю володіє кожне раціональне число?

9. Які числа називаються ірраціональними?

ІІ конкурс «Хто краще лічить усно?»

Оцінювання: правильна відповідь команди з першого разу – 2 б., виправлення – 1 б., виправлення другої команди – 1 б.

а)                              г)

б)                              д)

в)                                       е)

ІІІ конкурс «Бліц-турнір»

За допомогою проектора по черзі проектуються кожній команді завдання. Члени команди повинні знайти помилку у розв’язанні, пояснити її, виправити, розв’язавши правильно. Отже, знайти і виправити помилки, щоб не робити своїх.             

Оцінювання: помилка, пояснення і розв’язання – 5 б., помилка і пояснення – 3 б., розв’язання – 2 б.

Завдання для першої команди (розв’язують обидві).

Завдання: Знайти значення виразу при .

Розв’язання: при будь-якому значенні .

Помилка: добування коренів з-під кореневого виразу в квадраті.

Правильне розв’язання: .

Якщо , то .

Завдання для другої команди.

Завдання: Знайти значення виразу при .

Розв’язання: Якщо , то .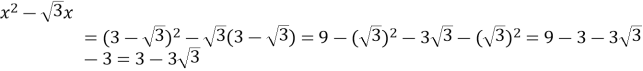

Помилка: 1. При піднесенні до квадрата різниці двох виразів пропущений подвоєний добуток. 2. При розкритті дужок, коли попереду стоїть знак мінус, знаки в дужках не змінено на протилежні.

Правильне розв’язання: Якщо , то .

Чи можна було розв’язати дану вправу по-іншому? (Спростити початковий вираз, винісши за дужки).

 ІV конкурс «Це цікаво знати»

На першому уроці, вводячи означення і позначення арифметичного кореня, ми говорили, що для того, щоб дізнатися прізвище вченого, який ввів сучасне позначення кореня і в якому році це відбулося, ми скористаємося знаряддям самого вченого, тобто дізнаємося про це, навчившись робити деякі операції та дії з квадратними коренями.

Вперше було введено математичне позначення квадратного кореня в 1525 році автором першого підручника з алгебри на німецькій мові німецьким вченим Рудольфом.

 

1	2	3
4	5	6
7	8	9

Але тоді воно мало вигляд такого ж самого знака, тільки без горизонтальної риски, тобто a. Пізніше горизонтальну риску ставили поряд, але  окремо, тобто       . Сучасний знак ввів французький вчений, прізвище якого вам відомо з курсу математики 6 класу, алгебри 7 класу, згадувати його ми будемо і на уроках геометрії в 9 класі.

А) щоб дізнатися, в якому це було році нам необхідно розв’язати «магічний» квадрат. А чому він так називається? (пояснення учнів)

Магічну суму біля дошки знаходить представник першої команди, дев’ятий елемент другої команди.

;

№9: .

Решта елементів таблиці – самостійно.

Оцінювання: перші три роботи; учень, який виконав першим, приносить своїй команді  3 бали, другим – 2 б., третім – 1 б.

У древні часи виготовляли амулети з магічними квадратами. Їх власникам гарантувались успіх у всіх справах і безпека. Такий «магічний» амулет був своєрідним талісманом. Переможець цього конкурсу також отримує у подарунок амулет (дарується амулет).

Щоб дізнатися, в якому році було введено сучасне позначення кореня, необхідно четвертий елемент таблиці (без літери a) піднести до квадрату і до знайденого результату додати 17.

(рік)

Б) Щоб дізнатися прізвище вченого, який ввів даний математичний символ, необхідно зіграти в «поле чудес».

Дана робота – робота групами і по рівнях за підручником (підручник з алгебри для 8 класу для загальноосвітніх навчальних закладів, автор Істер О.С.).

Оцінювання: команда, що виконає завдання першою отримує 2 бали; другою – 1 бал.

1

2

3

4

5

6

592 (1)           592(2)            598(1)             598(2)            603(1)            604(1)

 

 1 ком.  592(1)              598(1)            603(1)

 2 ком.  592(2)              598(2)            604(1)

                                    середній рівень         достатній рівень       високий рівень

 За таблицею многокутника, маючи корені рівняння, учні знаходять літери, які відповідають кореням.

 №592(1)             №592(2)

                                                                   

                                                                

   Д                                                      Е

 №598(1)                   №598(2)

                                                                       

                                                                    

                              К                                                       А

 №603(1)            №604(1)

                                                                     

                                                                  

   Р                                                         Т

Таблиця многокутника

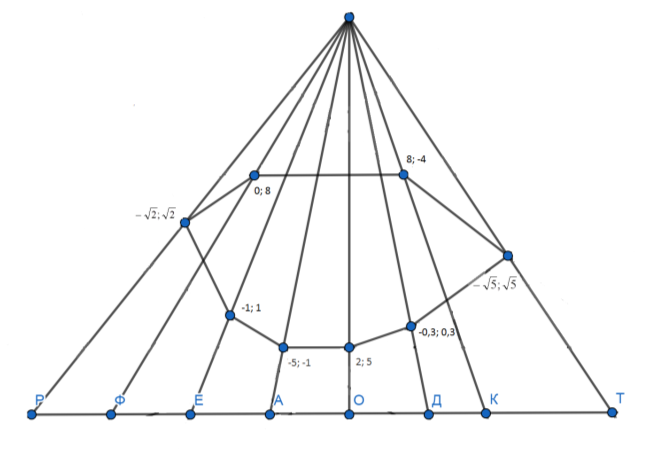
 V конкурс «Щасливий вибір»

 Представники команд вибирають картки із завданнями для команди-суперника. Серед усіх карток одна «щаслива» (без завдання). Для якої команди витягнута «щаслива» картка – та команда автоматично отримує 3 бали.

 Картка №1

 1. Позбутися ірраціональності в знаменнику дробу:

 

 2. Спростити вираз, якщо , .

 .

 3. Скоротити дріб:

 .

Картка №2

1. Позбутися ірраціональності в знаменнику дробу:

.

2. Спростити вираз, якщо .

.

3. Скоротити дріб:

.

Команди працюють «по бар’єрах», самостійно кожен учень.

На виконання – 6 хвилин. Потім обмінюються розв’язаними картками з сусідом. Представники так званого «нещасливого» вибору коментують розв’язання кожної вправи ( за 1 вправу 1 бал), учні виправляють помилки один в одного, на полях ставлять «+» - правильно, «-»- неправильно, потім повертають картки господарю. Господар проставляє цифру – кількість «+», картки збираються і віддаються журі. Кількість «+» - це кількість балів, які кожен член команди приніс своїй команді.

Якщо жодна  з команд не зробила «щасливого» вибору, то кожна з них отримує своє завдання (картка 1 і 2) та розв’язує його. В іншому разі весь клас розв’язує завдання «нещасливого» вибору (картка 1 або 2).

VІ конкурс «Робота в парі»

По одному представнику від кожної команди на дошці з різних сторін розв’язують одне і те ж завдання в парі. Клас те ж саме. Потім кожен із учнів рецензує по одному із завдань суперника, виправляє помилки і ставить оцінку. Ця оцінка – бали для команди. Рецензію журі також оцінює по п’ятибальній системі. Ці бали рецензент здобуває для своєї команди.

Завдання: Довести, що дане число раціональне.

 а) ;

 б) ;

VІІ конкурс «Домашнє завдання»

Всі зошити раніше зібрані і перевірені по командах. Той, хто перевіряв, доповідає про типові помилки.

Оцінювання: вся команда виконала правильно – 12 б., виконала все, але є помилки – 8 б., якщо є члени команди, які не виконали, то «-» 1 бал за кожного, хто не виконав.

3. Домашнє завдання (за підручником).

Повторити §15-18, розв’язати №741, 756, 762, .

4. Підсумок уроку (аналіз допущених помилок, виставлення оцінок).

5. Слово журі (визначення команди – переможниці; оголошення Міс Точність, Міс Активність, Міс Ввічливість (або Містер); нагородження).

6. Заключне слово вчителя. Який би не був результат конкурсу, головний результат – це ті знання, які ви здобули і які залишаться з вами назавжди. Подяка гостям за те, що прийшли, журі – за їх працю, учням – за урок.

Закінчити урок хочеться, можливо, вам відомими і традиційними словами, але такими простими і зрозумілими. Щиро від усього серця хочеться побажати всім присутнім у класі. Нехай у вашому житті все буде, як у математиці: щастя нехай додається, горе – віднімається, достаток множиться, а любов ділиться навпіл і взаємно.