Конспект уроку з алгебри для 9 класу на тему " Квадратний тричлен. Розкладання квадратного тричлена на множники""

Додаток В

Урок алгебри в 7 класі

Тема: Розкладання многочленів на  множники; виникнення та розквіт

            Київської Русі

Мета: - узагальнення та систематизування  знання учнів з теми: «Розкладання  многочленів на множники  та про історичні події та особистості з історії Київської  Русі»

         - розвивати в учнів навички використання вивчених способів розкладання  многочленів на множники та вміння  аналізувати про історичні факти і події

         - виховувати інтерес до наукових знань з різних предметів, повагу до історії  України

Тип уроку:  узагальнення та систематизація знань

Хід уроку

І. Організаційний момент.

1. Мета.

2. Вступ (проводить учитель історії)

Вправа «Мій настрій тут і тепер»

Мета: рефлекси.

Учням пропонують визначити свій настрій на початку уроку за допомогою умовних позначок погоди:

•             Сонячно   

 

•             Хмарно 

 

 

 

•             Нежить

 

На дошці закріплено плакат з позначками. Кожен учень по черзі говорить речення «Мій настрій зараз відповідає…» (називається відповідно настрою позначення).

Вчитель оцінює на плакаті  під відповідною позначкою кількість зазначених станів і пропонує 2-3 учням пояснити, чому у них такий стан. Після чого робить підсумок, що ми всі різні і наші стани також різні. Це нормально. Але давайте на нашому уроці спробуємо покращити настрій та не втратити сонячної погоди.

Вчитель говорить про те, що наш урок незвичайний. Він об’єднує два предмети: математику та історію. Тому давайте спробуємо визначити, чи є щось спільне у цих предметів.

 

Вправа: («Мозковий штурм»)

«Що є спільного між математикою і історією»

На дошці записується питання і всі учні по черзі, або за бажанням проговорюють свої ідеї, щодо цього запитання (ідеї можуть бути самі фантастичні), Один учень фіксує їх на дошці.

Наука

Пізнання

Цифри, дати

Математика-історія              

                                                                           Римські цифри

Особистості

 

Цікаво

Групуємо

Аналізуємо

Видатні діячі

 

Коли всі ідеї зібрано, колективно вибираємо ті, що дають відповідь на запитання.

Тепер давайте доведемо, що між математикою та історією є дійсно спільне, що об’єднує ці предмети.

ІІ. Робота в  малих групах.

Об’єднуємо учнів у групи (4 по 8 чоловік). Для об’єднання в групи всі по черзі говорять математичні та історичні терміни:

• культура
• рівняння
• держава
• вираз

                  Учні сідають по групах (в коло «пліч-о-пліч). В групі розподіляються ролі слідуючим чином:

• спікер – керівник групи
• секретар – веде записи
• посередник – стежить за часом, заохочує до роботи
• доповідач – доповідає про результати роботи групи

Для забезпечення швидкого та ефективного включення учнів і інтерактивну діяльність можна групам роздати пам’ятку для учнів, яка містить опис алгоритму діяльності).

Учитель на дошці вивішує плакат, записані назви команд і надалі запитуватимуться результати відповідей кожної команди. За кожну правильну відповідь - 3 бали.

Вчитель математики: А зараз кожна команда отримує завдання на карточках. Вирішивши математичні завдання повинні записати на листочках відповіді на завдання:

 

І команда

Розкласти многочлен на множники:

1. а² + а⁵                                                                                          
2. 2х – 1 + 4х (2х – 1)
3. 9 – а²b²
4. 0,24х⁵ + 0,36х³ – 0,48х⁴
5. 3а + 3b – a³ – a²b

(2х – 1) (1 + 4х)	О
а2 (1 + а3)	Х
(а + b) (3 – a2)	В
0,12x3 (2x2 – 4x – 3)	И
(3 – ab) (3 + ab)	Р

 

ІІ команда

 Розкласти многочлен на множники

1. 36х² у – 18 ху
2. 5а (а – b) + (а – b)
3. а² + 4а + 4
4. 0,6а² b ³ + 0,4а⁴ b ² - 0,2 а³ b ³
5. 4а – 2 b + 2а² - а b

 

(5a + 1) (a – b)	К
18xy (2x – 1)
(2a – b) (2 + a)	Й
(a + 2)2	И
0,2 a2b2 (3b + 2a2 –ab)

 

ІІІ команда

 Розкласти многочлен на множники

1. 7х⁶ у – 7 х³
2. a² + а –  2(а + 1)
3. а²⁴ - 25
4. 0,12а⁴ b ³ - 0,6а⁵ b ² + 0,24 а³ b ²
5. 3а + 3 b - 2аb - 2а²

(a + b) (b– 4a)	ДЬ
0,6a3b2 (2ab – a2 4)	І
7x3 (x3 – 1)	Л
(a2– 5) (a2 + 5)	Б
(a + 1) (a – 2a)	И

 

ІV команда

Розкласти многочлен на множники:

1. a⁵ + а⁴                                                                                          
2. 3a – 6b + a (a – 2b)
3. 1 – 2а + a²
4. 0,18х⁶ - 0,45х⁴ – 0,27х⁵
5. 6b² + 3ab – 4ab – 6a²

 

(1 – a)2	Е
0,9 x4 (2x2 – 5 – 3x)	К
(2b + 3a) (3b – 2a)
a4 (a + 1)	Щ
(a – 2b) (3 +a)

 

Доповідачі кожної команди приносять результати і відповіді записують на дошці. Це імена князів: Кий, Щек, Хорив, Либідь.

Учитель історії: Наступне завдання для груп: використавши карту покажіть місто Київ, коротко перекажіть легенду пов’язану з іменем цих князів.

Спікери команд організовують роботу. Команда, яка перша підготувалась відповідає, а інші доповнюють . вчитель історії оцінює відповіді, результати заносяться до таблиці.

Учитель математики: З давніх часів до нас дійшли уривки літописів, на яких стерлися дати, щоб визначити з яких часів вони дійшли до нас потрібно виконати наступне завдання. Спікери отримують завдання.

 

І команда

Розв’язати рівняння:

1) 4х² – 4х  = 0

2)( 9х² – 9) –( х² + х )= 0                   (1; 0; 1; 9)

 

ІІ команда

Розв’язати рівняння:

1) 6 m² - 6 m  = 0

2) (х² – 5х) (4х +20) =0                     (1; 0; 5; 4)

 

ІІІ команда

Розв’язати рівняння:

1) 5а² – 10а + 5 = 0

2)( х²  - 3х )+( 3 – х) = 0                     (1; 1; 1; 3)

 

ІV команда

 

Розв’яжіть рівняння:

1) 3х²  - 6х + З = 0

2) (х² -  2х) + (10 – 5х )= 0                      (1; 1; 2; 5)

 

  Вчитель математики: Доповідачі запишіть на дошці послідовно свої відповіді. Корені рівнянь і є роками правління князів, яких потрібно назвати (Це Я. Мудрий та В. Мономах).

Вчитель історії оцінює відповіді та заносить результати до таблиці. Після виконання завдання проводимо «мікрофон». На дошці закріплюють портретні зображення Я. Мудрого та В. Мономаха.

Вчитель історії: Дайте відповідь на запитання: «Який внесок в історію нашого краю вніс В. Мономах та Я. Мудрий?

Заслуховуються  відповіді учнів.

Вчитель математики. Які способи  розкладання на множники ви застосували при розв’язанні рівнянь і які способи ви ще знаєте?

Заслуховуються  відповіді учнів.

Вчителі підбивають підсумки цього завдання і заносять до таблиці. Підбиваються підсумки.

Вправа: «Мій  настрій тут і тепер». Піднімають руки діти, у кого змінився настрій: Розповідають який був, який став. Чому?

ІІІ. Домашнє завдання.

З історії: скласти історичний портрет Я. Мудрого та В. Мономаха.

З математики: скласти кросворд на тему: «Розкладання многочленів на множники»

ІV. Підсумок уроку.

Вчитель історії. Наша взаємодія на уроці допомогла повторити та узагальнити наші знання з математики та історії України.

 

 

 

 

 

 

 

 

 

 

Урок алгебри в 9 класі

Тема: Квадратний тричлен. Розкладання квадратного тричлен на множники.

Формування компетентностей:

предметна компетентність: сформулювати поняття квадратного тричлена, його коренів, формувати вміння розкладати квадратний тричлен на множники; формувати вміння застосовувати формулу до спрощення виразів;

Ключові компетентності:

спілкування державною мовою: доречно та коректно вживати в мовленні математичну термінологію, розвивати культуру математичних записів;

уміння вчитися впродовж життя: визначити мету навчальної діяльності, прагнути до вдосконалення результатів своєї діяльності , розвивати логічне мислення, увагу, вміння аналізувати, робити висновки;

Соціальну та громадянську компетентності: аргументувати та відстоювати свою позицію, виховувати самостійність, наполегливість, взаємоповагу, вміння працювати в команді; виховувати уважність, самостійність, взаємоповагу, любов до математики.

Очікувані результати: учні повинні  знати формулу розкладання квадратного тричлена на множники та вміти застосовувати її.

Тип уроку: урок засвоєння нових знань із застосуванням інтерактивних технологій.

Форма уроку: групова.

Хід уроку

І. Організаційний момент:

1. Позитивна установка на роботу:

Вчитель:  Кожна людина бажає бути успішною. А для цього успіху потрібні знання, велике значення має настрій, з яким ми прийшли на урок. Нагадую, що наш оптимізм запорука успіху, а посмішка – найкоротша відстань до людини.

Тема сьогоднішнього уроку «Розкладання квадратного тричлена на множники». На уроці ми з’ясуємо що таке квадратний тричлен, яке значення змінної називається коренем квадратного тричлена. Скільки коренів може мати квадратний тричлен і навчимося розкладати квадратний тричлен  на множники.

А за девіз нашого уроку ми взяли вислів Гете.

Вчитель: Свої навчальні досягнення ви вносите в картку самоконтролю, де в останній колонці оціните свою роботу по рейтинговому принципу і не забудьте відмітити об’єм засвоєного матеріалу.

Картка самооцінювання

Прізвище _______________________________________________

 

1. Ви брали активну участь в роботі групи (0 – 2 б) …………………….
2. Ви вносили вдалі пропозиції, які врахувала група (0 – 2 б) ………….
3. Ви висунули цілком нову ідею (0 – 2 б) ……………………………….
4. Мікрофон (1 б) …………………………………………………………..
5. Таблиця (1 б) ……………………………………………………………..
6. Термінологічне лото (1 б) ………………………………………………
7. Оцінка ……………………………………………………………………
8. Рівень засвоєння матеріалу
9.  

ІІ. Актуалізація опорних знань

1. Перевірка домашнього завдання ( 2 учні розв’язують вправи, аналогічні до розв’язаних удома)

1 учень.

1) Звести до зведеного квадратного рівняння:

                3х² – 24х + 21 = 0

2) Знайти корені рівняння за т. Вієта.

                х² – 10х + 21 = 0

3) Розв’язати рівняння:

               2х² – 5х + 3 = 0

2 учень.

 1) Звести до зведеного квадратного рівняння:

                0,25х² – 2х + 4 = 0

2) Знайти корені рівняння за т. Вієта.

                х² – 16х + 15 = 0

3) Розв’язати рівняння:

               5х² – 2х - 3 = 0

А тим часом ми повторимо все, що ми знаємо про квадратні рівняння:

1. Які рівняння називаються квадратними?

2. Як називаються числа a,b,c.

3. За допомогою чого ми взнаємо скільки коренів має квадратне рівняння.

4. За якою формулою знаходиться дискримінант?

5. Яким може бути дискримінант в порівнянні з 0?

6. Скільки коренів має квадратне рівняння, якщо Д > 0?

7. Скільки коренів має квадратне рівняння, якщо Д = 0?

8. Скільки коренів має квадратне рівняння, якщо Д < 0?

9. Які ще квадратні рівняння ви знаєте?

10. Які рівняння називаються зведеними? (якщо перший його коефіцієнт = 1)

11. Як ми розв’язували зведені квадратні рівняння.

12. Записати т. Вієта

А зараз перевіримо, як наші учні справилися із завданнями: (учні біля дошки коментують свої відповіді)

1 учень.

1.  х² – 8х + 7 = 0.

2.

х₁ = 3; х₂ = 7

3. 2х² – 5х + 3 = 0

Д = (-5)² – 4*2*3 = 25 – 24 = 1

х_{1 =}        х₂ = 

2 учень.

1. х² – 8х + 16 = 0

2.

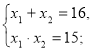
х₁ = 1;   х₂ = 15.

3. 5х² + 2х – 3 = 0

Д = 2² – 4*5 * (-3) = 4 + 60 = 64

х₁ =       х₂ =

ІІІ. Вивчення нового матеріалу

Вчитель: У математиці та прикладних науках важливу роль відіграє функція, яку можна задати рівністю у = ах² + bх + с.

У правій частині рівності – квадратний тричлен

Квадратний тричлен називається многочлен виду ах² + bх + с, де х – змінна, а,b, с – числа, причому а 0.

Змінну квадратного тричлена можна позначити будь-якою буквою. Наприклад:      4х² – 5х + 6;

                         у² + 4у – 7;

                         ;

Якщо квадратний тричлен прирівняти до нуля, матимемо квадратне рівняння його корені й дискримінант – називають коренями і дискримінант даного квадратного тричлена. Як на вашу думку дізнатись чи має корені і скільки їх у квадратному тричлені

Теорема: Дано: х₁ і х_{2 –} корені квадратного тричлена

                       ах² + bх + с

                 Довести: ах² + bх + с = а (х – х₁) (х – х₂)

Доведення:

1. Подано квадратний тричлен у вигляді а (х² + )

 

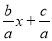2. За т. Вієта:

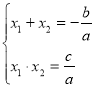     або 

   - (х₁ + х₂)

3. Маємо х² + =

= х² – (х₁ + х₂)х + х₁*х₂ =

= х² – х*х₁ – х* х₂ + х₁*х₂ =

= х (х – х₁) – _х2 (х – х₁) =

 = (х – х₁) (х – х₂)

4. Отже, ах² + bс + с = a (х – х₁) (х – х₂)

ІV. Закріплення нових знань та вмінь учнів.

Вчитель: А тепер розглянемо приклад:

Розкладання квадратного тричлена на множники

Прочитайте розв’язання прикладу 1 і зрозумійте його.

1. Розкласти тричлен 2х² – 5х + 3 на множники.

          Рзв’язання

Розв’яжемо квадратне рівняння:

2х² – 5х + 3 = 0,

D = (-5)² – 4*2*3 = 25 -24 = 1,

х_{1 =}        х₂ = 

Отже, 2х² – 5х + 3 = 2 (х – 1,5)(х – 1).

Закінчи розв’язання прикладу 2.

2. Розкласти тричлен 5у² + 2у – 3 на множники

       Розв’язання

5у² + 2у – 3 = 0

D = 2² – 4 * 5 (-3) = ….,

у₁ = …..;      у₂ = ……

5у² + 2у – 3 = 5 (у – у₁) (у – у₂) = 5 ( у - …) (у + …)

Завдання: Кожен опрацьовує самостійно. Розкласти квадратний тричлен на множники доводиться при скороченні дробів, зведенні їх до спільного знаменника.

Наприклад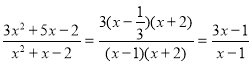

3х² + 5х – 2 = 0

D = (-5)² – 4*3*(-2) = 25 + 24 = 49

х₁ =

х₂ =

х² + х – 2 = 0

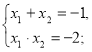
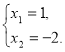
А тепер попрацюємо в групах

Розкласти квадрат тричлена на множники

Запам’ятайте

ах² + bc + с = а (х – х₁)(х – х₂)

де х₁,х₂ – корені рівняння ах² + bх + с = 0

1. Розкласти на множники:

а) 3х² + 2х – 1

б) 49с² – 42с + 9

2. Скоротити дріб:

а)

б)

3. Спростити вираз:

Термінологічне лото (із різних складів скласти математичні терміни)

Підсумок уроку

1. Що нового ви дізнались на уроці?
2. Із математичних термінів скласти алгоритми розкладання многочленна на множники.

 

Домашнє завдання: №174 (1,2 ст) – початковий і середній рівень

                                    №174 (3 ст) + №175 (1ст) – достатній рівень

                                    №175 – високий рівень