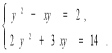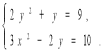Конспект уроку з алгебри для 9 класу"Розв’язування систем рівнянь другого степеня з двома змінними і задач."
Конспект уроку для 9 класу з алгебри , який можно використовувати при вивченні теми "Системи рівнянь і нерівностей", з використанням різних форм самостійної роботи і використанням групової роботи на уроці.
Алгебра, 9 клас
Тема 4. СИСТЕМИ РІВНЯНЬ І НЕРІВНОСТЕЙ
Тема уроку: Розв’язування систем рівнянь другого степеня з двома змінними і задач.
Мета уроку:
• Навчальна: узагальнити і систематизувати знання учнів про способи розв'язування систем рівнянь другого степеня, перевірити і відкоригувати вміння і навички учнів розв'язувати системи рівнянь другого степеня, розв'язувати задачі за допомогою систем рівнянь другого степеня.
• Розвивальна: розвивати навички індивідуальної та групової самоорганізації, розвивати математичну мову, обчислювальну техніку, розумову активність, логічне мислення, інтерес до предмету.
• Виховна: виховувати в учнях впевненість в своїх силах, акуратність, охайність, уважність, прагнення до самовдосконалення та саморозвитку.
Обладнання: таблиця, презентація, картки для індивідуальної роботи.
Тип уроку. Комбінований урок.
Епіграф:
Послухайте - і Ви забудете, подивіться - і Ви запам'ятаєте, зробіть - і Ви зрозумієте!
(Конфуцій)
Хід уроку.
1. Організаційний етап.
а) Привітатися, відзначити відсутніх.
б) Записати дату, тему уроку.
в) Запропонувати учням визначити мету та задачі уроку.
2. Перевірка домашнього завдання.
Частково розв'язки завдань записати на дошці. Учні виконують самоперевірку з дошки, вчитель вибірково перевіряє правильність виконання завдань в зошитах.
3. Актуалізація опорних знань.
1. Фронтальне опитування: повторити основні способи розв'язування систем рівнянь другого степеня:
- графічний спосіб,
- спосіб підстановки,
- спосіб додавання,
- спосіб введення нової змінної.
Також повторити:
- застосування формул скороченого множення при розв'язуванні систем рівнянь 2 ступеня,
- розв'язування систем, які містять однорідні рівняння,
- розв'язування систем з параметром.
2. Усне виконання вправ (презентація).
Визначити, який спосіб раціонально застосувати під час розв'язування систем рівнянь. Згадати алгоритми розв'язування систем рівнянь різними способами.
1)  2)
2)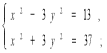 3)
3) 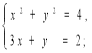 4)
4) 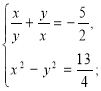
5) 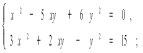 6)
6) ![]() 7)
7) 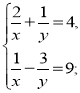 8)
8) 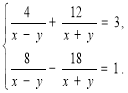
Відповіді:
1) спосіб підстановки,
2) спосіб додавання,
3) графічний спосіб,
4) спосіб введення нової змінної,
5) 1 рівняння системи - однорідне рівняння, необхідно розділити на![]() ,
,
6) спосіб підстановки,
7) спосіб додавання,
8) спосіб введення нової змінної.
Учні пропонують хід розв'язання кожної системи.
4. Перевірка та корекція знань, вмінь і навичок учнів.
I. Розв'язування систем рівнянь другого степеня.
а) Учні, які працюють на достатньому і високому рівнях, отримують картки для індивідуальної роботи.
б) Інші учні виконують самостійну роботу.
Картки для індивідуальної роботи.
4 учнів працюють біля дошки.
Картка № 1.
Розв'язати способом підстановки.
![]()
Відповідь: ![]()
Картка № 2.
Розв'язати способом додавання.
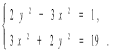
Відповідь: ![]()
Картка № 3.
Розв'язати систему способом введення нової змінної.
![]()
Відповідь: ![]()
Картка № 4.
Розв'язати систему графічним способом.
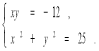
Відповідь: ![]()
Кілька учнів виконують завдання за картками на місцях.
Картка № 5.
Скільки розв'язків в залежності від значення параметра має система рівнянь?
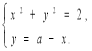
Відповідь:
1) 2 розв'язки, якщо ![]()
2) 1 розв'язків якщо ![]()
3) Немає розв'язків, якщо ![]()
Картка № 6.
Розв'язати систему.
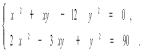
Відповідь: ![]()
Учні виконують взаємоперевірку, задають один одному додаткові питання.
Самостійна робота за варіантами з наступною взаємоперевіркою (розв'язки заздалегідь записані за відкидній дошці).
|
1 варіант Розв'язати системи рівнянь: |
2 варіант Розв'язати системи рівнянь: |
|
1.
Відповідь:
2.
Відповідь: |
1.
Відповідь:
2.
Відповідь: |
Для тих, хто впорається з самостійною роботою раніше, додаткове завдання.
Розв'язати систему:
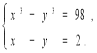
Відповідь: ![]()
Перевірити розв'язки, підвести підсумки.
II. Розв'язування задач за допомогою систем рівнянь другого степеня.
Учні працюють в групах. Всього 6 груп; 1 і 4, 2 і 5, 3 і 6 групи отримують однакові завдання. Група, яка розв'яже задачу першою, основні етапи розв'язання записує на дошці. Перед початком роботи в групах, познайомити учнів з історичною довідкою.
Історична довідка (презентація).
Те, що системи рівнянь другого степеня, можна використовувати в різних завданнях, помітили ще в давнину. У текстах, які були написані ще в III - II тисячоліттях до н.е., є чимало задач, які розв'язували за допомогою систем рівнянь. Наприклад, задача Діофанта: «Площі двох своїх квадратів я додав: ![]() Сторона другого квадрата дорівнює
Сторона другого квадрата дорівнює ![]() сторони першого і ще 5.» Відповідна система рівнянь сьогодні:
сторони першого і ще 5.» Відповідна система рівнянь сьогодні: 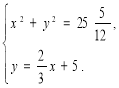
Діофант Александрійський - видатний давньогрецький математик, який жив в Александрії. «Арифметика» Діофанта складалася з 13 книг, але збереглися тільки 6 перших. Велика частина праці - це збірник задач з розв'язками (збереглися 189 задач). На прикладах розв'язування задач автор демонстрував загальні методи. Діофант досліджував системи рівнянь другого степеня і розглядав різні варіанти розв'язування таких систем. Розглянуті їм методи можна використовувати для розв'язування рівнянь вищих ступенів. Діофант був настільки відомим математиком, що навіть епітафія на його могильному камені була написана у вигляді задачі. Там було зазначено: «Подорожній! Під цим каменем покоїться прах Діофанта, який помер в глибокій старості. Шосту частину довгого життя він був дитиною, дванадцяту - юнаком, сьому - провів неодруженим. Через п'ять років після одруження у нього народився син, який прожив удвічі менше батька. Через чотири роки після смерті сина заснув вічним сном і сам Діофант. Скажи, якщо вмієш рахувати, скільки років прожив Діофант? »
Задачі для роботи в групах.
Задача 1.
Два працівника, працюючи разом, можуть виконати завдання за 4 години. За якийсь час може виконати завдання кожен працівник самостійно, якщо один з них може це зробити на 6 годин швидше, ніж інший?
Задача 2.
Площа прямокутника дорівнює 120 см2, а периметр - 46см. Знайдіть сторони прямокутника.
Задача 3.
З двох сіл, відстань між якими дорівнює 50 км, виїхали одночасно назустріч один одному два велосипедиста і зустрілися через 2 години. Знайдіть швидкість кожного велосипедиста, якщо один з них витратив на весь шлях з одного села в інше на 1 годину 40 хв менше, ніж інший.
Відповіді:
Задача 1. 15см і 8см.
Задача 2.15км / ч і 10км / год.
Задача 3.10ч і 15год, 12год і 12год.
5. Підведення підсумків уроку.
- Що повторили на уроці?
- Що нового дізналися на уроці?
- Чи допоміг вам урок систематизувати знання і вміння ?
Хочу ще раз підкреслити, що дуже важливо повторювати вивчене, «відточувати» свої знання. На підтвердження своїх слів розповім вам притчу.
До майстра прийшов учень і запропонував: - «Учитель! Ви досягли найвищих результатів у знаннях, спіткали Бога, а чи так само Ви унікальні в своїх діях? Я більше ніж упевнений, що володію сокирою краще Вас і зможу перемогти, якщо ми вирішимо позмагатися. Дерев, вирубаних мною, буде набагато більше.
Учитель був спокійний і сказав: - «Я готовий».
Пішли вони в ліс. Учитель і учень вибрали собі по ділянці і розпочали змагання. Учень без відпочинку рубав дерева, раз у раз він чув, що вчитель не рубає. Учень думав, що він відпочиває і радів. Але після закінчення змагання виявилося те, що більше зрубаних дерев у вчителя.
І він вигукнув: - «Як це Вам вдалося? Адже я чув, як Ви час від часу переставали рубати ».
Учитель відповів: «Так, в цей час сокиру потребував заточування».
Дійсно, іноді варто вкласти свій час, докласти зусиль для того, щоб відточити свою майстерність на шляху до успіху.
-Я вам бажаю успіху в подальшому вивченні теми і, щоб швидше його досягти, пропоную виконати наступне домашнє завдання.
6. Домашнє завдання.
1.Розв'язати системи рівнянь:
а) графічним способом
![]()
б) способом підстановки
![]()
в) способом додавання
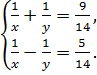
2. Розв'язати задачу Діофанта ( за бажанням).


про публікацію авторської розробки
Додати розробку