Комунальний заклад «Навчально-виховне об’єднання І-ІІІ ступенів  «Науковий ліцей Міської ради міста Кропивницького Кіровоградської області»

 

 

 

 

 

 

 

 

 

 

КОНСПЕКТ УРОКУ з алгебри у 9 класі на тему:

«Арифметична прогресія»

 

 

Підготувала вчитель математики, спеціаліст вищої категорії,  к.п.н. Ботузова Ю.В.

 

Дата проведення: __________

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2019 рік

Мета уроку: сформувати поняття арифметичної прогресії; познайомити з основними властивостями арифметичної прогресії; продемонструвати прикладну спрямованість змісту теми. Створити творчу атмосферу учнівському колективі; виховувати навички групової та самостійної роботи, сприяти розвитку ерудиції і світогляду учнів.

Продовжити        роботу        над    формуванням     предметних компетентностей:

логічну – здатність використовувати математичну та логічну символіку на практиці; здатність логічно обґрунтовувати та доводити математичні твердження; здатність застосовувати математичні методи при розв’язанні практичних задач; здатність здійснювати дедуктивні обґрунтування правильності розв’язання задач та шукати логічні помилки у неправильних дедуктивних міркуваннях.

Методологічну– здатність аналізувати ефективність розв’язання задач математичними методами; рефлексія власного досвіду розв’язування задач. Продовжити роботу над формуванням ключових компетентностей:

соціальну та громадянську– аргументовано й грамотно висловлювати

власну думку, дотримуватися правил етики, співробітництва; уміння вчитися впродовж життя–вміти визначати мету навчальної діяльності, аналізувати, оцінювати результати своєї навчальної діяльності, правильність власних суджень або приймати свої помилки; розвивати вміння учнів створювати математичні моделі до роз’язування задач; самоосвіти та саморозвитку – сприяти розвитку навичок самостійно працювати з різними джерелами інформації, розвивати уяву, пам’ять, логіку, нестандартність мислення, вміння узагальнювати, порівнювати, навички роботи з ІКТ. Очікувані результати:

Учні повинні знати: способи задання послідовностей, зокрема аналітична та рекурентна формули; означення арифметичної прогресії, визначення різниці арифметичної прогресії; формули загального члена послідовності, суми n перших членів арифметичної прогресії; властивості арифметичної прогресії.

Учні повинні вміти: застосовувати одержані знання при розв’язуванні задач, аналізувати умову задачі та використовувати теорію при її розв’язуванні.

Тип уроку: урок засвоєння нових знань.

Обладнання: підручник – Алгебра: підруч. для 9 кл. загальноосвіт. навч. закладів/ А.Г. Мерзляк, В.Б. Полонський, М.С. Якір. – Х.: Гімназія, 2017. – 272 с.; інтерактивна дошка (презентація); інтерактивні вправи на повторення числових послідовностей; інтерактивна вправа на встановлення відповідності між прогресією та її різницею.

ХІД УРОКУ: І. Організаційний етап.

ІІ. Перевірка домашнього завдання. Вчитель перевіряє наявність виконаного домашнього завдання в учнів. Учні, за потреби, ставлять запитання, щодо виконання домашніх вправ. Вчитель вичерпно відповідає на запитання учнів.

ІІІ. Формулювання теми, мети та завдань уроку. Мотивація навчальної діяльності.

Давайте подумаємо разом, де в повсякденному житті ми зустрічаємо послідовності чисел? (діти наводять власні приклади – номери будинків на вулицях, послідовність цифр в номері телефону тощо) 

Інколи ми можете встановити певну закономірність в цих послідовностях, інколи не можемо. 

Проходячи тести на встановлення рівня інтелекту – тести IQ, зустрічаємо запитання на доповнення заданих послідовностей чисел, при цьому ми маємо помітити певну закономірність. Наприклад, запитання такого типу (рис.1, рис.2). Пропонуємо учням дати відповіді на запитання тесту IQ.

 

 

 

 

IV. Актуалізація опорних знань

Проводиться фронтальне опитування за матеріалом попередньої теми:

«Числові послідовності».

Запитання (на презентації):

-                                                                                           як позначаються послідовності та їх члени?

-                                                                                           яка послідовність називається скінченною?

-                                                                                           яка послідовність називається нескінченною?

-                                                                                           способи задання послідовностей. 

 

Завдання (на презентації): Визначити способи задання послідовностей:        а ) ( а_n ): 0,1; 0,02; 0,003; 0,0004; 0,00005.

       б )  ( b_n ): дільники числа 24.

 

n	1	2	3	4
хn	12	24	36	48

      в ) 

 

 

          г ) a_n  = 13n;      b_n = 2 n – 1.

          д ) a_n+1 = a_n +3, а₁ = 2.

Cкінченні чи нескінченні дані послідовності? Зростаючі чи спадні?

Додаткові запитання до завдань:

-                                                                                           назвіть третій член послідовності?

-                                                                                           який номер має член, що дорівнює ____?

-                                                                                           який член є наступним за числом _____? - який член є попереднім до числа _______?

 

 

V. Сприйняття та осмислення нового матеріалу (у формі лекції):

Основні теоретичні відомості про арифметичну прогресію

Арифметична прогресія

Означення. Числова послідовність, кожний член якої, починаючи з другого, дорівнює сумі попереднього з одним і тим самим даним для послідовності числом, називається арифметичною прогресією. Позначають арифметичну прогресію a_n.

a_n1  a_n d – рекурентна формула арифметичної прогресії;

Число d  a_n1 a_n називається різницею арифметичної прогресії. a_n  a₁ n1d – формула nго члена арифметичної прогресії. Для різниці арифметичної прогресії є й така формула: d _ an  am . n  m

При d 0 арифметична прогресія є зростаючою; при d 0 – спадною; при d 0 – постійною.

Властивості арифметичної прогресії

1.      Будь-який член арифметичної прогресії, починаючи з другого, дорівнює середньому арифметичному двох рівновіддалених від нього членів прогресії, тобто

an  anm  anm або an am  2anm .

                                                                                           2                                       ₂

2.      Сума двох членів         скінченної арифметичної      прогресії,

рівновіддалених від її кінців, є величиною сталою, тобто

a1 an  ak an1k  const.

Ознаки арифметичної прогресії

-                      Якщо будь-який член числової послідовності, починаючи з другого, дорівнює середньому арифметичному двох будь-яких рівновіддалених від нього членів послідовності, то така числова послідовність є арифметичною прогресією;

-                      Якщо сума будь-яких двох членів скінченної числової послідовності, рівновіддалених від її кінців, є величиною сталою, тобто a₁ a_n  a_k a_n1k  const, то така послідовність є арифметичною прогресією.

-                      Якщо nий член послідовності визначається лінійною від n функцією, тобто a_n  dnb, то числова послідовність є арифметичною прогресією, причому кутовий коефіцієнт d – є різницею арифметичної прогресії.

 

Сума S_n  a₁ a₂ ...a_n називається сумою перших n членів арифметичної прогресії:

а) Sn  a1  an n; 2

б) Sn  2a1  n 1d n.

2

VІ. Первинне закріплення нового матеріалу:

Виконання вправ з підручника. №16.1.° Серед поданих послідовностей укажіть арифметичні прогресії:

1)  3, –6, 12, –24; – не прогресія;

2)  4, 8, 12, 16; – прогресія;

3)  5, 10, 5, 10; – не прогресія;

4)  42, 39, 36, 33; – прогресія;

5)  –5, –3, –1, 1; – прогресія;

6)  1,2; 1,3; 1,5; 1,6 – не прогресія;

Виконання інтерактивної вправи на дошці

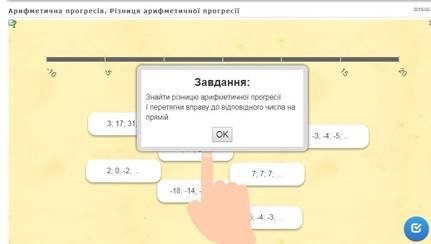
                Вправа        1.        Знайти        різницю       арифметичної        прогресії:

https://learningapps.org/4646217

 

 

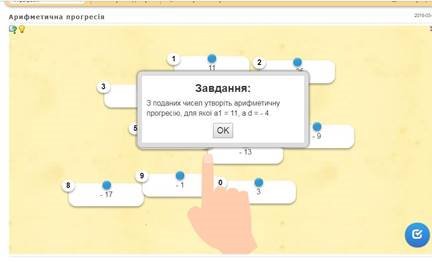
Вправа 2. З поданих чисел утворіть арифметичну прогресію:

https://learningapps.org/4752145

 

№ 16.3.° Знайдіть чотири перші члени арифметичної прогресії, перший член якої дорівнює 1,2, а різниця становить –0,3.

Розв’язання: 

Використовуючи означення арифметичної прогресії та її рекурентний спосіб задання, отримаємо:

а₁=1,2; d=-0,3; а₂= а₁+d=1,2+(-0,3)=0,9; а₃= а₂+d=0,9+(-0,3)=0,6; а₄= а₃+d=0,6+(-0,3)=0,3. Відповідь: 1,2; 0,9; 0,6; 0,3.

 

№ 16.5.° Перший член арифметичної прогресії (a_n) дорівнює 4, а різниця становить 0,4. Знайдіть: 1) a₃; 2) a₁₁; 3) a₃₂.

Розв’язання: a₁=4, d=0,4.

Використовуючи формулу n-ого члена арифметичної прогресії, знайдемо:

1)   a₃=a₁+2d=4+2∙0,4=4+0,8=4,8;

2)   a₁₁=a₁+10d=4+10∙0,4=4+4=8; 3) a₃₂=a₁+31d=4+31∙0,4=4+12,4=16,4.

Відповідь: a₃= 4,8; a₁₁=8; a₃₂=16,4.

 

№16.7.° Знайдіть різницю та двісті перший член арифметичної прогресії        2,6; 2,9; 3,2; ... .

Розв’язання: a₁=2,6; a₂=2,9; a₃=3,2

Використовуючи означення арифметичної прогресії, поняття різниці арифметичної      прогресії     (формули), а        також          формули     n-ого члена арифметичної прогресії, виконуємо завдання:

d=a₂-a₁=2,9-2,6=0,3.

a₂₀₁=a₁+200d=2,6+200∙0,3=2,6+60=62,6. Відповідь: d=0,3; a₂₀₁= 62,6.

 

№16.12. Знайдіть формулу n-го члена арифметичної прогресії:  1) –5, –7, –9, –11, ...;                                       3) a², 2a², 3a², 4a², ...; Розв’язання:

1) a₁=-5; d=-7-(-5)=-2; → a_n=-5+(n-1) ∙d;

3) a₁=a²; d=2a²-a²=a²; → a_n= a²+(n-1) ∙a²; → a_n= a²+n∙a²- a²; → a_n= n∙a² Відповідь: 1) a_n=-5+(n-1) ∙d; 3) a_n= n∙a².

 

№ 16.13. Чи є членом арифметичної прогресії (c_n): 1) число 20,4, якщо c₁ = 11,4, а різниця прогресії d = 0,6; 2) число 38, якщо c₁ = 8, а різниця прогресії d = 1,4?

У разі ствердної відповіді вкажіть номер цього члена.

 Розв’язання: Скористаємось формулою n-ого члена арифметичної прогресії для знаходження номера n. Якщо значення n буде натуральне, то задане число є членом арифметичної прогресії, якщо n – не ціле, або ж від’ємне, то задане число – не є членом арифметичної прогресії. 

1)                 Нехай с_n=20,4, c₁ = 11,4, d = 0,6; маємо рівність: 20,4=11,4+(n-1)∙0,6; → 9=0,6(n-1); → 9=0,6n-0,6; → 0,6n=9,6; →n=16. Отже, число 20,4 є 16-им членом арифметичної заданої прогресії;

2)                 Нехай с_n=38, c₁ = 8, d = 1,4; маємо рівність: 38=8+(n-1)∙1,4; → 30=1,4n-1,4; → 1,4n=31,4; → n≈22,43. Таким чином, число 38 не є членом заданої арифметичної прогресії, бо отримане значення n – не натуральне. Відповідь: 1) 16-й член прогресії; 2) не є членом прогресії.

 

№16.15. Знайдіть другий член арифметичної прогресії, якщо перший і третій члени дорівнюють відповідно –6 і 12.

Розв’язання: Скористаємось властивістю арифметичної прогресії, а anm  anm a1  a3 6 12 саме: an  , a2     9.

                                       2                         2             2

Відповідь: 9.

 

№16.17. Знайдіть перший член арифметичної прогресії (b_n), якщо: 

b₅ = 11, b₁₁ = –7.

 

І спосіб                                                    ІІ спосіб

Знайдемо    різницю      арифметичної Складемо систему двох рівнянь з прогресії за формулою:       двома невідомими (b₁ та d); bn bm b11 b7               7 11           18        b₅ b₁  4d;          11b₁  4d;

d                       3.            →∙    →n  m         115    6          6          _b₁₁ b₁ 10d;   _7 b₁ 10d;

Знайдемо а₁, взявши один із заданих Віднімемо ці два рівняння, маємо:

членів послідовності та знайдену 186d ; d=-3. різницю:      b₁=b₅-4d=11-4∙(-3)=11+12=23.

b₅=b₁+4d; → 11= b₁+4∙(-3); →∙           →∙b₁=11+12=23.

Відповідь:∙b₁=23.

Задача про математичний квадрат та способи його заповнення:

 

 

№16.20. Скільки додатних членів містить арифметична прогресія 

5,2; 4,9; 4,6; ...?

Розв’язання: Скористаємось формулою n-ого члена арифметичної прогресії та складемо нерівність, враховуючі задані умови: a₁=5,2; a₂=4,9; тоді d=4,9-5,2=-0,3 та a_n>0.

a_n=5,2+(n-1)∙(-0,3)>0; →∙5,2-0,3n+0,3>0; →∙-0,3n>-5,5; →

Відповідь: 18.

 

№ 16.23. Між числами –6 і 3 вставте п’ять таких чисел, щоб вони разом із даними числами утворювали арифметичну прогресію.

 Розв’язання: спочатку запишемо сформульовану в задачі умову до такої таблиці:

n	1	2	3	4	5	6	7
an	-6	a2	a3	a4	a5	a6	3

 

Скористаємось властивістю формулою різниці арифметичної прогресії, а також означенням арифметичної прогресії:

d  an am  a7 a1  36  9 1,5. nm    71      6          6

Заповнимо таблицю:

n	1	2	3	4	5		6	7
an	-6	-4,5	-3	-1,5		0	1,5	3

VІІ. Підбиття підсумків уроку

VІІІ. Домашнє завдання

Вивчити конспект. Знати матеріал §3 п.16. Виконати вправи за підручником: №16.4, №16.6, №16.11, №16.14, №16.22.

 

Додаткове домашнє завдання (для учнів з високим рівнем навчальних досягнень і всіх бажаючих):

№1. Знайдіть п’ятий та дев’ятий члени арифметичної прогресії (а_n), сума n перших членів якої дорівнює S_n n² 2n1. 

Розв’язання:

S₁  1 2 1 2,



                _S₅  25 52 1 14,                  

S5  2a1  4d 5  22  4d 5  14.

                                    2                     2

                 d  12;a₅  212^4  14;a₉  2                 .

                                     5                    5           5

 

№2. Сума перших трьох членів арифметичної прогресії дорівнює 15, сума трьох останніх дорівнює 78, а сума всіх членів прогресії дорівнює 155.

знайдіть числа, що утворюють прогресію.

Розв’язання:

a1  an  15 78  31.Sn  a1  an n 155; n 10.a1 a2 a3 15,

                                            3                                 2                                           a8 a9 a10  78.

               3a₁  3d 15,    d  3;a₁  2. 

_3a₁  24d  78.

Отже, послідовність: 2, 5, 8, 11, 14, 17, 20, 23, 26, 29 – шукана арифметична прогресія.

Її загальний член дорівнює: a_n  2n13.