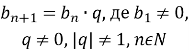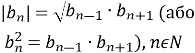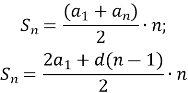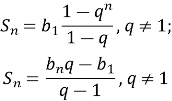Конспект уроку з алгебри на тему: "Числові послідовності"
Конспект уроку алгебри в 9 класі студентки групи МІЕ17Б Чудної Олени
Тема: Числові послідовності
Мета:
-
Навчальна:
- Повторити, систематизувати й узагальнити знання та вміння учнів з теми «Числові послідовності» (знання основних понять та формул, вміння використовувати їх при розв’язуванні типових задач);
- Встановити зв’язки даної теми з іншими розділами курсу алгебри
-
Розвивальна:
- Розвивати логіку, пам’ять, нестардатність мислення;
- Розвивати вміння узагальнювати та порівнювати;
- Розвивати компетентності саморозвитку та самоосвіти;
- Розвивати вміння математично грамотно висловлювати думки;
- Розвивати вміння правильно формулювати математичні твердженя.
-
Виховуюча:
- Виховувати наполегливість, допитливість, відповідальність;
- Виховувати інтерес до навчання;
- Виховувати інтерес до математики
Тип уроку: узагальнення та систематизації знань.
План уроку
- Організаційний етап. (2 хв.)
- Перевірка домашнього завдання. (2 хв.)
- Мотивація навчальної діяльності. (2 хв.)
- Актуалізація опорних знань. (9 хв.)
- Узагальнення і систематизація вмінь. (25 хв.)
- Підсумок уроку. (3 хв.)
- Постановка д/з. (2хв)
Хід уроку
- Організаційний етап.
Привітання вчителя. Перевірка готовності учнів до уроку. Перевірка присутніх на уроці (відмітити в журналі).
- Перевірка домашнього завдання.
Задача 1.Купівля коня.
(Із арифметики Магницького.)
Продавець продав коня за 156 крб. Але покупець, придбавши коня, передумав і повернув його господарю, кажучи: "Нема мені користі купувати за таку ціну коня, який таких грошей не вартий". Тоді продавець запропонував інші умови: "Якщо ціна за коня дуже висока, то купи лише цвяхи для його підков, а коня одержиш безкоштовно на додачу. Цвяхів у кожній підкові 6. За перший дай мені всього 1/4 к., за другий – 1/2 к., за третій - 1к. і т. д..." Покупець, спокусившись низькою ціною та бажаючи безкоштовно придбати коня, прийняв умови, думаючи, що за цвяхи доведеться заплатити не більше 10 крб. На скільки покупець проторгувався?
Розв’язання
За умовою маємо геометричну прогресію, де ![]() .
.
Всього цвяхів з підков буде: ![]()
Тобто, в прогресії буде 24 члени.
Нам треба знайти суму цих 24 членів послідовності, це сума яку повинен буде заплатити покупець за підкови:
![]()
![]()
![]()
Покупець проторгувався на:
![]()
Відповідь: покупець проторгувався на 41797 крб.
Задача 2.
Мешканець маленького містечка був відомий своєю скнарістю. Коли у нього були справи в повітовому місті, розташованому в 25 км від цього містечка, він звичайно шукав сусідів, які б підвезли його. Одного разу скнара крутився на площі, шукаючи того, хто підвіз би його за спасибі додому. Але цього разу нікого не було і він змушений був шукати платного візника. Скнара обійшов їх усіх, торгуючись з ними і порівнюючи ціни. Один просив 250 крб., другий - 200 крб., третій -150. Усі ці ціни здалися йому занадто високими. Нарешті він помітив візника з убогим візком і жалюгідною шкапою. Коли скнара запитав його скільки він візьме за дорогу, той подивився на землю, почухав потилицю і відповів: "за 1-й кілометр заплати мені 1 коп., за другий - 2 коп, за 3-ій - 4, за 4-ий - 8 і так до кінця шляху."
"От дурний - подумав скнара, ледве стримуючи сміх, - лічить на копійки." Поспіхом він заліз у візок і гукнув:"Згідний! Поїхали!"
Скільки грошей він повинен заплатити за дорогу?
Розв’язання
Маємо геометричну прогресію: 1; 2; 4; 8 …;
![]()
![]()
Щоб з’сувати скільки коштувати така поїздка, треба знайти суму 25 членів геометричної прогресії (так як їхати 25 км):
![]()
![]()
![]()
Відповідь: скнара повинен буде заплатити за поїздку 335544 крб 31 коп.
Задача 3.
Турист, підіймаючись на гору, за першу годину досяг висоти 800 м, а за кожну наступну годину піднімався на висоту , на 25 м меншу, ніж за попередню. За скільки годин він досягне висоти 5700 м?
Розв’язання
Маємо арифметичну прогресію, де ![]()
Задача зводиться до знаходження ![]() .
.

![]()
![]()
![]()
Перевірка:
![]()
![]()
Відповідь: турист досягне висоти 5700 м за 8 годин.
Задача 4.
У змаганні зі стрільби за кожен промах у серії з 25 пострілів стрілок одержував штрафні очки: за перший промах – одне штрафне очко, а за кожен наступний – на 0,5 очка більше, ніж за попередній. Скільки разів влучив у ціль стрілок, що одержав 7 штрафних очків?
Розв’язання
Маємо арифметичну прогресію, де ![]()
Знайдемо ![]() з формули суми, таким чином з’ясуємо кількість промахів:
з формули суми, таким чином з’ясуємо кількість промахів:
![]()

Отже, стрілок зробив 4 промахи. Таким чином в ціль він влучив: ![]()
Відповідь: стрілок влучив в ціль 21 раз.
Задача 5.
Одного разу розумний бідняк попросив у скупого багатія притулку на два тижні за таких умов: «За це я тобі першого дня заплачу 1 крб, другого – 2, третього – 3 і т.д., збільшуючи щоденну плату на 1 крб. Ти ж будеш подавати милостиню: першого дня 1 копійку, другого – 2, третього – 4 і т.д., збільшуючи щодня милостиню вдвічі». Багатій з радістю на це згодився, вважаючи умови вигідними. Скільки грошей одержав багатій?
Розв’язання
З’ясуємо спершу скільки карбованців заплатив бідняк багатію. Ми маємо арифметичну прогресію, де ![]()
![]()
![]()
Отже бідняк заплатить 105 крб.
Тепер вияснимо скільки заплатить милостині багатій. Маємо геометричну прогресію, де ![]()
![]()
![]()
![]()
Таким чином виходить, що багатій має сплатити 163,86 крб.
Виходить, що багатій не те, що не одержав грошей, він ще й поніс витрати у розмірі: ![]()
Відповідь: багатій не заробив грошей, натомість витратив 58,83 крб.
- Мотивація навчальної діяльності.
Ми з вами розглянули дуже цікаву тему «Числові послідовності» і з’ясували, що вони насправді підстерігають чи не на кожному кроці нашого життя: це й штрих-коди, і послідовність нот на нотному стані, і навіть слова це певна послідовність літер.
Не оминули нас і особливі послідовності, такі як, арифметична та геометрична прогресії, а також нескінченно спадна геометрична прогресія.
Ви вивчили всі основні поняття щодо них. Та, найціннішим є вміння використати набуті знання.
- Актуалізація опорних знань.
Та перш, ніж ми приступимо до розв’язання задач, пригадаємо теорію. Гадаю всі вирішували кросворди, та чи ви пробували себе колись в антикросвордах? Отож, завдання таке: скласти питання до записаних у кросворді математичних понять.
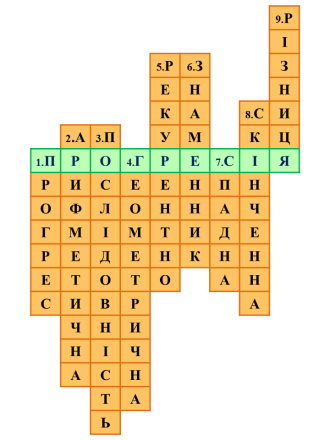
- Слово «прогресія» у перекладі з латинської означає «рух вперед» або…
- Послідовність, кожний член якої, починаючи з другого, дорівнює попередньому, доданому до одного й того самого числа, називають … прогресія.
- Нескінченна або скінченна сукупність чисел.
- Послідовність відмінних від нуля чисел, кожне з яких, починаючи з другого, дорівнює попередньому помноженому на одне й те саме число називають … прогресія.
- Спосіб задання прогресії формулою.
- Стале число, множенням на яке утворюється кожний наступний член геометричної прогресії.
- Послідовність, у якій кожний наступний член менший за попередній.
- Послідовність, яка містить скінченну кількість членів.
- Число, додаванням якого утворюється кожне наступне число у арифметичній прогресії.
Поки клас вирішує анти кросворд (він виводиться на слайді) до дошки викликається два учні, вони записують на бічних дошках формули до арифметичної/геометричної прогресій.
|
Арифметична прогресія |
|
Геометрична прогресія |
|
|
Рекурентна формула |
|
|
|
Формула n-го члена |
|
|
|
Характеристична властивість |
|
|
|
Формула суми n перших членів |
|
|
|
Формула суми всіх членів геометричної прогресії (|q|<1) |
|
- Узагальнення і систематизація вмінь.
Тепер, коли ми все пригадали, саме час використати наші знання на практиці.
- Знайти тридцять перший член заданої прогресії: 3; 5,5; 8;…
Розв’язання
![]()
![]()
Отже, це арифметична прогресія з різницею ![]()
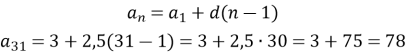
Відповідь: ![]()
- Знайти суму перших тринадцяти членів арифметичної прогресії -8; -5; -2;…
Розв’язання
![]()
Знайдемо різницю прогресії:
![]()
Тепер можемо знайти суму:
![]()
Відповідь: ![]()
- Між числами 3 і 7 вставте два числа таких, щоб вони разом з даними утворювали арифметичну прогресію.
Розв’язання
Нехай ![]()
Знайдемо різницю прогресії з формули n-го члена:
![]()
![]()
![]()
Тоді,
![]()
![]()
Відповідь: ![]()
-
Послідовність
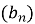 – геометрична прогресія. Знайдіть
– геометрична прогресія. Знайдіть 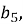 якщо
якщо 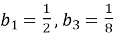 і
і 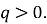
Розв’язання
![]()
Знайдемо знаменник прогресії:
![]()
![]()
![]()
![]() – сторонній корінь, за умовою
– сторонній корінь, за умовою
![]()
Відповідь: ![]()
-
Знайдіть суму шести перших членів геометричної прогресії
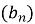 , у якої
, у якої 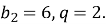
Розв’язання
![]()
Знайдемо ![]() :
:
![]()
![]()
Отже,
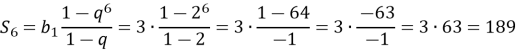
Відповідь: ![]()
-
Знайти суму нескінченно спадної геометричної прогресії
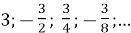
Розв’язання
![]()
Знайдемо знаменник прогресії:
![]()
Отже,
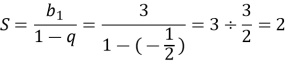
Відповідь: ![]()
-
Підсумок уроку.
Ми проробили чималу роботу, тепер в мене є до вас декілька питань:
- Завдання якого характеру ми виконували? (на знаходження n-го члена арифметичної/геометричної прогресій, знаходження суми n перших членів арифметичної/геометричної прогресій, знаходження суми нескінченно спадної геометричної прогресії).
- Які завдання виявилися найскладнішими? Чому?
- Як ви оцінюєте свою роботу на уроці?
- Чи задоволені ви попередніми результатами вивчення теми «Числові послідовності»?
Молодці. Дякую за ваші відповіді. На наступному уроці ви напишете контрольну роботу і я зможу оцінити наскільки добре ви засвоїли тему.
Вчитель виставляє оцінки за урок.
- Домашнє завдання.
Підготуватися до контрольної роботи: повторити всю теорію, що вивчали на попередніх уроках (послідовності, арифметична/геометрична прогресія та її властивості, сума n перших членів арифметичної/геометричної прогресії, сума всіх членів нескінченно спадної геометрично прогресії); виконати Домашню контрольну роботу №4 на ст.188-189 (Алгебра: підруч. Для 9-го кл. загальноосвіт. навч. закл. / О.С. Істер. – Київ : Генеза, 2017. – 264 с.) з поясненнями, не просто варіанти відповідей.
Домашня контрольна робота №4
-
Послідовність задано формулою
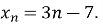 Знайдіть
Знайдіть 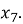
|
А. 7; |
Б. 14; |
В. -7; |
Г. 28 |
![]()
- Укажіть послідовність, що є арифметичної прогресією:
|
А. 2; 4; 6; |
Б. 2; 4; 5; |
В. 0; 1; 8; |
Г. 1; 3; 9. |
![]()
- Укажіть послідовність, що є геометричною прогресією:
|
А. 0; 1; 8; |
Б. 4; 5; 6; |
В. 1; 2; 4; |
Г. -2; -3;-4. |
![]()
- Тіло за першу секунду подолало 15 м, а за кожну наступну – на 2 м більше, ніж за попередню. Яку відстань подолало тіло за сьому секунду?
|
А. 30 м; |
Б. 24 м; |
В. 3 м; |
Г. 27 м. |
![]()

-
Знайдіть суму десяти перших членів арифметичної прогресії
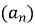 , якщо
, якщо 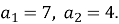
|
А. -130; |
Б. -65; |
В. -100; |
Г. 65. |
![]()
![]()
![]()
-
Знайдіть п’ятий член геометричної прогресії
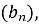 якщо
якщо 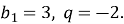
|
А. 24; |
Б. -96; |
В. -48; |
Г. 48. |
![]()
![]()
-
Послідовність
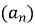 – арифметична прогресія,
– арифметична прогресія, 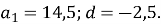 Укажіть число, яке є членом цієї прогресії.
Укажіть число, яке є членом цієї прогресії.
|
А. -21; |
Б. -22; |
В. -23; |
Г. -24. |
![]()
Підставимо замість ![]() запропоновані числа:
запропоновані числа:
-
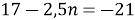
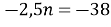
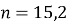 , не задовольняє, так як
, не задовольняє, так як 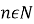
-
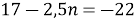
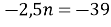
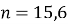 , не задовольняє, так як
, не задовольняє, так як 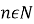
-
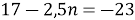
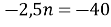
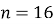 , задовольняє
, задовольняє 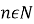
-
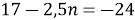
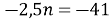
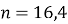 , не задовольняє, так як
, не задовольняє, так як 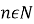
- Знайдіть суму натуральних чисел, які кратні числу 8 і не перевищують числа 400.
|
А. 20400; |
Б. 10600; |
В. 10200; |
Г. 9800. |
8; 16; 24; 32; …– арифметична прогресія
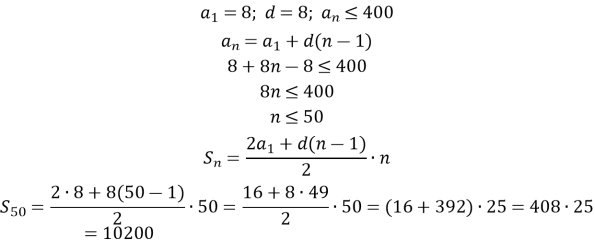
-
Послідовність
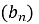 – геометрична прогресія. Знайдіть
– геометрична прогресія. Знайдіть 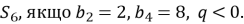
|
А. -21; |
Б. 21; |
В. 63; |
Г. -63. |
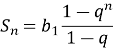 Знайдемо
Знайдемо ![]() За характеристичною властивістю:
За характеристичною властивістю:
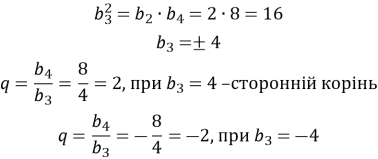
Тоді
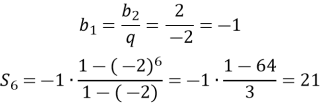
-
Знайдіть найменший член послідовності
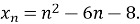
|
А. -16; |
Б. -17; |
В. -18; |
Г. Такого члена не існує |
![]() Так як коефіцієнт при
Так як коефіцієнт при ![]() більше нуля, то вітки параболи будуть дивитися вгору, а найменшого свого значення функція набуватиме у вершині.
більше нуля, то вітки параболи будуть дивитися вгору, а найменшого свого значення функція набуватиме у вершині.

-
Послідовність
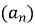 – арифметична прогресія. Знайдіть
– арифметична прогресія. Знайдіть 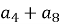 , якщо
, якщо 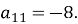
|
А. Знайти неможливо |
Б. -4; |
В. -16; |
Г. 16. |
За властивістю геометричної прогресії
![]()
![]()
![]()
-
При яких значеннях
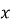 числа
числа 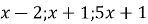 є послідовними членами геометричної прогресії?
є послідовними членами геометричної прогресії?
|
А. 3; |
Б. -3; |
В. 0,25; -3; |
Г. -0,25; 3. |
Скористаємось характеристичною властивістю геометричної прогресії:
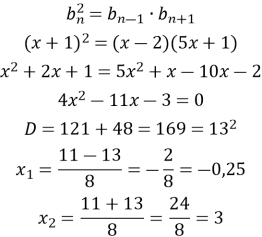


про публікацію авторської розробки
Додати розробку