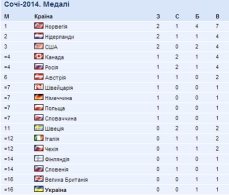
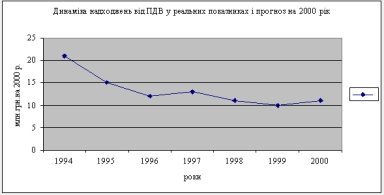
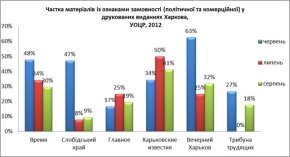
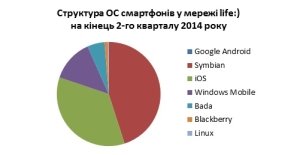
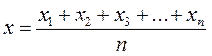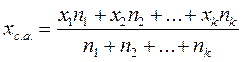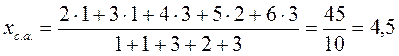Статистичні дані. Способи подання даних.

Математична статистика — розділ математики, який присвячений методам збору й обробки математичних даних та їх використанню для наукових і практичних спостережень.

Статистичне дослідження складається з кількох етапів:

1. Збирання даних.
2. Оброблення даних та їх подання у зручній формі (у вигляді таблиці, графіку, діаграми).

3. Аналіз даних.
4. Висновки та рекомендації.

Основні поняття математичної статистики:

1. Статистичні дані — сукупність чисел, які дають кількісну характеристику ознак певних об'єктів та явищ, що нас цікавлять.

2. Відібрану для спостереження сукупність об'єктів називають вибірковою сукупністю або вибіркою.

3. Кількість об'єктів сукупності називають об'ємом сукупності.

4. Числа, що є значеннями ознак кожної групи, на які можна поділити вибірку, називають варіантами; послідовність варіант називають варіаційним рядом.

5. Частоти — числа, які показують, скільки разів повторювалось кожне значення ознаки сукупності.

6. Відносна частота – відношення частоти до об'єму вибірки.

Приклад. Нехай дано вибірку: 2; 2; 2; 3; 3; 3; 3; 3; 4; 4; 4; 4; 4; 4; 5; 5; 5; 5; 5; 6. х1 = 2; х2 = 3; х3 = 4; х5 = 5; х6 = 6 — варіанти вибірки; 2; 3; 4; 5; 6 — варіаційний ряд.

Частота варіанти х1 дорівнює 3; варіанти х2 — 5; варіанти х3 — 6; варіанти х4 — 5; варіанти х5 — 1. Відносна частота варіанти х1 дорівнює  = 15%; варіанти х2 — = 25%.

Для обробки статистичних даних виконують їх зведення, тобто упорядковують, узагальнюють статистичні дані.

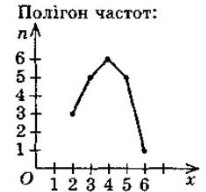
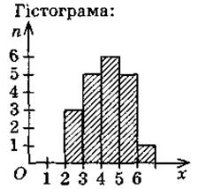
Способи зведення статистичних даних:

1) складання статистичного ряду;

2) складання статистичної таблиці розподілу вибірки;

3) складання полігона частот;

4) складання гістограм.

Приклад. Економіст, аналізуючи тарифні розряди працівників одного із цехів заводу, вибрав документи 20 робітників і виписав з них послідовність чисел, що вказують на тарифні розряди: 4; 4; 3; 2; 5; 2; 3; 5; 4; 3; 3; 2; 5; 4; 5; 4; 6; 3; 4; 5 — вибірка, що піддається обробці.

Статистичний ряд цієї вибірки: 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6;

Статистична таблиця розподілу вибірки:

Тарифний розряд х1

2

3

4

5

6

Кількість робітників п

3

5

6

5

1

Вибірки характеризуються центральними тенденціями: середнім значенням, модою і медіаною

Середнє арифметичне значення

 , де xi — значення ознаки (варіанти); n — число одиниць сукупності; де x — середнє арифметичне значень xi ознаки.

Зважене середнє арифметичне значення

, де хi — варіанти; nі — частоти.

Мода вибірки — це значення ознаки, яка найбільш часто повторюється у вибірці.

Медіаною вибірки – варіанта, яка розміщена посередині варіаційного ряду.

Приклад. Дано вибірку вимірювання повітря температури (t, °С) у першу декаду квітня: 5; 6; 4; 3; 4; 5; 6; 2; 4; 6. Складіть статистичний ряд; визначте варіанти та їхні частоти; складіть варіаційний ряд, для якого знайдіть середнє зважене значення, моду та медіану.

Розв'язання:

Статистичний ряд даної вибірки: 2, 3, 4, 4, 4, 5, 5, 6, 6, 6.

Варіанти, варіаційний ряд: 2, 3, 4, 5, 6; частоти відповідно дорівнюють 1, 1, 3, 2, 3.

Середнє зважене значення:

Мода дорівнює 4 і 6, бо 4 і 6 повторюються найчастіше — по 3 рази.

Оскільки у варіаційному ряді 5 чисел: 2, 3, 4, 5, 6, то медіана дорівнює 4.