Тема уроку: Розв’язування тригонометричних рівнянь.

Мета уроку:

-   створити умови для вдосконалення вмінь та навичок розв’язувати

тригонометричні рівняння, поглибити знання про методи та прийоми розв’язування тригонометричних рівнянь;

-   сприяти розвитку розумової активности учнів, логічного мислення, навичок самостійної та групової діяльності;

-   продовжити роботу по вихованню в учнів культури спілкування, інтересу до математики.       

Тип уроку: урок застосування знань

                                         Хід уроку:

                I.       Організація класу.

1) Мотивація 

«Результат навчання дорівнює добутку здібностей та старанності. 

Якщо старанність дорівнює нулю, то і весь добуток дорівнює нулю.  А здібності є у кожного».

2) Повідомлення теми уроку

На попередніх уроках ви ознайомились з основними методами розв’язування тригонометричних рівнянь.

А зараз поміркуйте: яку мету ви ставите перед собою ?

Заповніть Лист самоконтроль (учні аналізують  свої  вміння та в кожному рядку ставлять позначку).

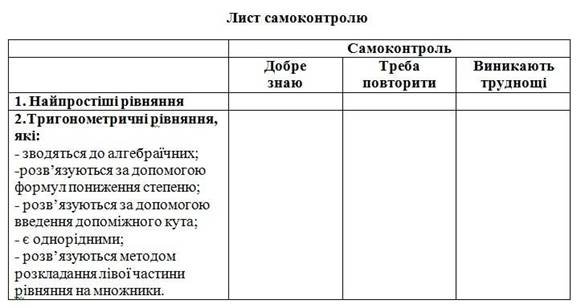
3) Ознайомлення з планом уроку

У кожного з вас є оціночний лист, в якому ви бачите етапи уроку та критерії оцінювання кожного етапу (додаток). 

                        ІІ. Актуалізація опорних знань

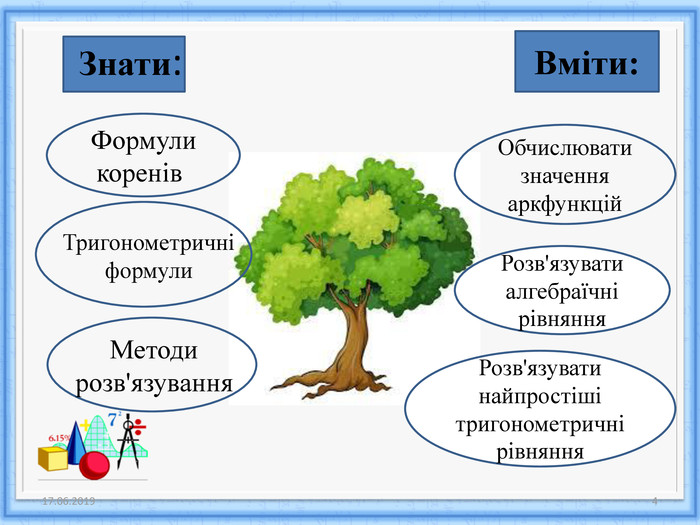
        Які знання  необхідні для розв’язування тригонометричних рівнянь? 

(формули коренів рівнянь, тригонометричні формули, методи розв’язування рівнянь)

Які вміння та навички  необхідні для розв’язування тригонометричних рівнянь?  (знаходити значення аркфункцій, розв’язувати найпростіші рівняння). Слайд заповнюється поступово, синхронно з відповідями учнів.

             Перевіримо, як ви володієте цими знаннями та вміннями.

1)  Математичний диктант с самоперевіркою

           (вправа на знаходження значень обернених тригонометричних функцій)

2)  Вправа «Продовж формулу». Самоперевірка.

3)  Вправа «Перевір  себе».

            Розв’язування найпростіших тригонометричних.              Учні отримують картки з завданням:

Самоперевірка.

4)  Встановлення відповідності.

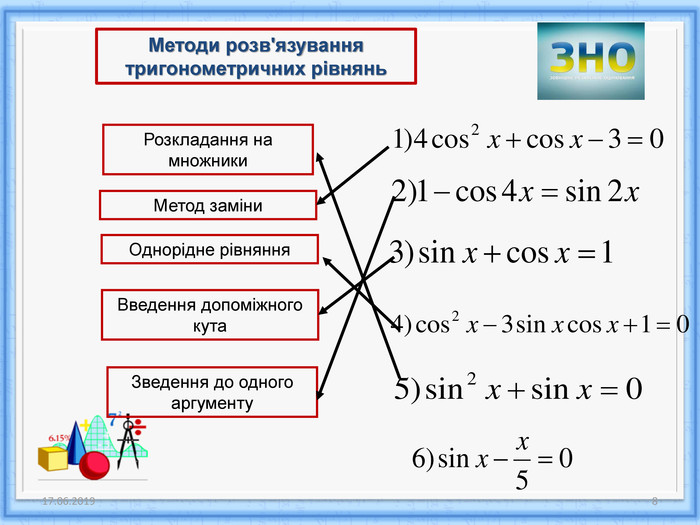
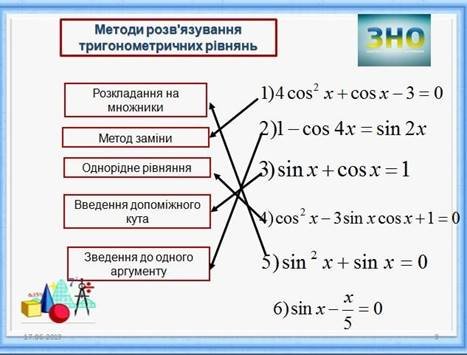
                   Які методи розв’язування тригонометричних рівнянь ви знаєте?    

(одночасно з відповідями учнів відкриваються методи на слайді)

                   Яким методом можно розв’язати кожне із рівнянь?

1)        sin² xsinx0

Розкладання на множники

2)        4cos² xcosx30                     Ділення на одну из функцій                                           

3)        cos² x3sinxcosx10              Введення допоміжної  змінної

4)        sinxcosx1 Введення допоміжного кута

 5)   1cos4xsin2x x

6)  ^{sin x} 5 ^{ 0}                               Скільки коренів має рівняння на проміжку 0;

Які із методів викликають труднощі?

Як ви гадаєте, чи всі методи перераховані? Пригадаємо алгоритм розв’язування тригонометричних рівнянь.

ІІІ. Основна частина

1)  Розв’язування типових рівнянь

            Розв’яжіть  рівняння №1-5 (за кожне правильно розв’язане рівняння учень отримує по 2 бали, перевіряє і оцінює вчитель).

2)  Групова робота  

Чи можливо розв’язати рівняння №6 одним з зазначених методів? (ні, потрібен інший)

x

                 ^{sin x} 5 ^{ 0}         Скільки коренів має рівняння на проміжку 0;

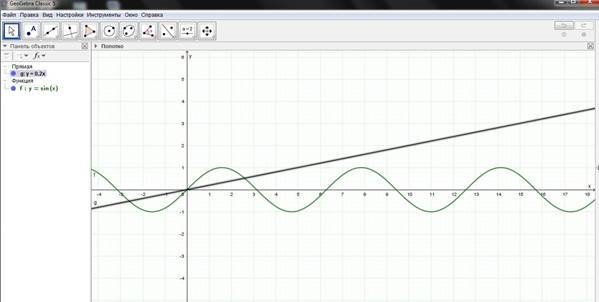
         Учні в групах обговорюють метод розв’язування рівняння, вносять пропозиції. Кожна группа пропонує свій метод розв’язування та демонструє розв’язок.

Перевірка відбувається за допомогою програми GeoGebra. Роботу кожного учня оцінює керівник групи (0-3 бали).

IV. Заключна частина

   (Схема початку уроку на слайді№4)

Що нового ми сьогодні дізнались?

Які ще вміння та навички  необхідні для розв’язування тригонометричних  рівнянь? ( властивості та графіки тригонометричних функцій)

Рефлексія    «Метод незакінчених речень»

Сьогодні на уроці  я…

Чи досягли ви мети, яку поставили на початку уроку?

Поставте позначки в Листі самоконтролю. Проаналізуйте, чи змінились результати на кращі.

Оцініть свою роботу, поставте оцінку в Оціночний лист.

Повідомлення домашнього завдання 

(розв’язування тригонометричних рівнянь)

Додаток

Оціночний лист учня 10-А класу

-------------------------------------------------

Таблиця оцінювання