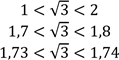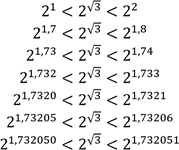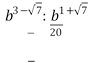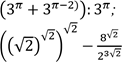Конспект уроку з алгебри та початків аналізу для 11 класу на тему: "Узагальнення поняття степеня. Степінь із дійсним показником"

Діяльність вчителя/вчительки/вчителів

Діяльність учня/учениці/учнів

Вкажіть, будь ласка, яка сьогодні в нас мета уроку?

Повторити поняття степеня та

За необхідності, вчитель, коригує мету, яку запропонували учні.

вивчені в 10 класі властивості степеня із раціональним показником, вивчити властивості степеня із дійсним показником.

Діяльність вчителя/вчительки/вчителів

Діяльність учня/учениці/учнів

Спочатку вчитель запитує про завдання, з якими виникли труднощі, а потім ходить по класу та проглядає зошити учнів, робить відповідні помітки.

Декілька учнів виконують завдання, з якими виникли труднощі в більшості, біля дошки з поясненнями.

Діяльність вчителя/вчительки/вчителів

Діяльність учня/учениці/учнів

Вчитель пропонує учням пригадати разом властивості степеня із раціональним показником, виконавши вправу в

LearningApps:

В 10 класі ви ознайомилися з поняттям степеня додатного числа з додатним показником. Тому для початку давайте пригадаємо раніше вивчені властивості.

Учні разом з вчителем виконують відповідну вправу.

Діяльність вчителя/вчительки/вчителів

Діяльність учня/учениці/учнів

Загалом степені з довільними дійсними показниками розглядали ще в XVII столітті окремо один від одного Лейбніц та Бернуллі.

Тож крокуючи вслід за ними, зараз ми з вами спробуємо з’ясувати, що ж розуміють під поняттям степеня числа 𝑎 > 1 із дійсним показником 𝛼.

          Для     початку      розглянемо      значення

степеня 2^√3.

Нам відомо, що √3 ≈ 1,7320508 … . 

Розглянемо десяткові наближення числа

√3 з недостачею та з надлишком:

Тому будемо вважати, що

𝑟 < √3 < 𝑠, 𝑟 ∈ ℝ, 𝑠 ∈ ℝ.

Звідси

2𝑟 < 2√3 < 2𝑠

Знайдемо за допомогою калькулятора

наближені значення для 2^√3 з недостачею та надлишком:

…

Як бачимо значення 2^𝑟 та 2^𝑠 наближаються до одного й того самого числа 3,32199 … . Це число і вважають

степенем 2^√3. Отже, 2^√3 ≈ 3,32199 … . Обчисліть значення 2^√3 на калькуляторі.

Тобто коли ми вибираємо раціональні числа 𝑟, які з недостачею наближаються до деякого ірраціонального 𝛼, та раціональні 𝑠, які з надлишком наближаються до цього самого ірраціонального числа 𝛼, для будьякого 𝑎 > 1 існує єдине число 𝑦, більше за всі 𝑎^𝑟 і менше від усіх 𝑎^𝑠. Це число 𝑦 і є значенням 𝑎^𝛼.

Аналогічно для будь-якого 0 < 𝑎 < 1, коли 𝑟 < 𝛼 < 𝑠, вважають, що 𝑎^𝑠 < 𝑎^𝛼 < 𝑎^𝑟.

Властивості степеня з раціональним показником діють і для степеня з ірраціональним показником.

3,3172782 < 2^√3 < 3,3403517

3,3218801 < 2^√3 < 3,3241834

3,3218801 < 2^√3 < 3,3221104

3,3219952 < 2^√3 < 3,3220182

3,3219952 < 2^√3 < 3,3219975

…

2^√3 ≈ 3,321997

Діяльність вчителя/вчительки/вчителів

Діяльність учня/учениці/учнів

Перейдемо до виконання завдань:

1. (учні відповідають усно з місця) Чи має зміст вираз:

1) (−3)^√3; 2) 0^√7; 3) 2^−2√2; 4) 0^−√5; 5) 5^√13?

1) Ні. 2) Так. 3) Так. 4)Так. 5) Так.

2. (біля дошки працює 1 учень) Знайдіть область допустимих значень виразу:

1)  𝑥^−√3;

2)  𝑥^√7;

3)  (2 − 𝑥)^−2√2;

            4)                   

5)

1) (0; +∞);

2) [0; +∞);

3) (−∞; 2);

4) (−∞; −1] ∪ [1; +∞); 5) [0; +∞).

3. (біля дошки працює 1 учень) Знайдіть значення виразу:

1)                                                                        ;

2)                                                                           ;

3)

1)  7;

2)  3;

3)  64.

4. (біля дошки працює по 1 учню на кожні 3 вирази) Спростіть вираз:

                                        2                                         2

            1)  (2 + 𝑎^√2)     − (2 − 𝑎^√2) ;

2)

3)                                              ;

4)                                              ;

√

5)                                              (𝑐^√5)      ;

6)                                              (2√2−1 + 2√2+1): 2√2;

7)

            8)                                ;

√

9)

1) 8𝑎^√2;

2) 𝑎^√7;

3) 𝑎²;

4) 𝑏2−2√7;

5) 𝑐¹⁰;

6) 2,5;

7)         ;

8) 1; 9) 0.

5. (біля дошки працює 1 учень) Вкладник поклав на депозит в банку 3000 грн. під 10 % річних. Яка сума буде на його рахунку через 3 роки, якщо в кінці кожного року гроші, нараховані за відсотками, не знімаються, а додаються до депозитного внеску?

Відповідь: 3993 грн.

6. (біля дошки працює 1 учень) Період напіврозпаду деякого ізотопа плутонія складає 140 діб. Визначте масу плутонія, що залишиться через 8 років, якщо його початкова маса становила 6 г. Радіоактивний розпад описують формулою:

Розв’язання.

𝑚₀ = 10 (г)

𝑡 = 2 ∙ (365 ∙ 3 + 366) = 2922 (доби)

;

𝑚(2922) ≈ 5,2 ∙ 10⁻⁶ (г)

 – маса радіоактивної

речовини в початковий момент часу  𝑡 = 0, 𝑚(𝑡) – її маса в момент часу 𝑡, 𝑇₀ – період напіврозпаду.

Відповідь: 5,2 ∙ 10⁻⁶ г.