Конспект уроку з алгебри та початків аналізу в 11 класі з теми "Логарифмічні рівняння"
Методична розробка уроку з алгебри і початків аналізу в 11 класі на тему «Логарифмічні рівняння»
Виконала: Гергішан Юлія Володимирівна
Тема уроку “ Логарифмічні рівняння”
Мета уроку:
- навчальна:
познайомити учнів з поняттям логарифмічного рівняння; розглянути основні методи розв’язання логарифмічних рівнянь; формувати вміння розв'язувати логарифмічні рівняння різними способами; удосконалити вміння обчислювати логарифми та застосовувати властивості логарифмів під час розв’язування рівнянь;
- розвивальна:
розвити логічне мислення, пам'ять, увагу, спостережливість, вміння аналізувати, порівнювати, робити висновки, лаконічно і точно висловлювати свою думку, узагальнювати, обґрунтовувати, виділяти головне; сприяти розвитку грамотної усної і письмової математичної мови;
- виховна:
виховати взаємоповагу в колективі, чуйне ставлення один до одного, вміння розуміти точку зору співрозмовника; виховувати культуру спілкування в колективі; прищепити інтерес до предмету.
Учні повинні:
- знати: означення логарифма, види логарифмів та їх основні властивості; властивості та графік логарифмічної функції, означення логарифмічного рівняння та основні методи їх розв’язання;
- вміти: обчислювати логарифми, використовувати властивості логарифмів при розв’язувані рівнянь; знаходити область визначення логарифмічної функції; вміти логарифмувати та потенціювати вирази; розв'язувати логарифмічні рівняння різними способами.
Тип уроку: засвоєння нових знань, умінь, навичок.
Міжпредметні зв’язки:
- Фізика.
- Біологія.
- Астрономія.
Хід уроку
- Організаційний момент.
- Перевірка домашнього завдання.
- Мотивація навчальної діяльності.
Девіз заняття: “Не достатньо мати лише добрий розум, Головне – це раціонально застосовувати його”
Рене Декарт
(Французький математик XVII ст.)
На минулих уроках ми познайомились з поняттям логарифма, з його видами та властивостями. Дізналися, який вигляд має логарифмічна функція та якими властивостями вона володіє. Переконалися в тому, що без знань логарифмів деякі види показникових рівнянь взагалі неможливо розв’язати. Сьогодні ми з’ясуємо, як, знаючи значення логарифма, знайти число, від якого береться логарифм, тобто вчитимемося розв’язувати логарифмічні рівняння. Отже, тема уроку – «Логарифмічні рівняння». Сьогодні ми познайомимось з означенням логарифмічного рівняння та зі способами їх розв’язування. Їх небагато. Якщо їх освоїти, то будь-яке рівняння з логарифмами буде посильне кожному з вас. Крім того, ці знання вам неодмінно знадобляться під час підготовки та складання Державної підсумкової атестації чи ЗНО.



 Крім цього, сьогодні на занятті ми будемо говорити ще й про такі речі (див. малюнки):
Крім цього, сьогодні на занятті ми будемо говорити ще й про такі речі (див. малюнки):
Я розумію ваше здивування. Виникають запитання:
- Що об’єднує ці малюнки?
- Чому вони присутні у нас на занятті?
- Як їх можна пов’язати з темами, що ми вивчаємо, і з математикою
взагалі?
Але щоб все це пояснити, та докорінно у всьому розібратися, давайте пригадаємо основний матеріал, який ми вивчаємо. Повторимо відомості про логарифми та їх властивості, оскільки вони дають змогу розв’язувати логарифмічні рівняння.
- Актуалізація опорних знань студентів.
Фронтальне опитування
- Усна вправа « Відтворіть означення» (Учням потрібно вставити пропущені слова та прочитати означення)
- Логарифмом числа b за основою а називається показник степеня, до якого потрібно піднести основу а, щоб отримати число b.
- Число, яке стоїть під знаком логарифма, повинне бути додатнім .
- Якщо основа логарифма а = 10 , то такий логарифм називається десятковим і позначається lg b.
- Якщо основою логарифма є число е≈2,728281…, то такий логарифм називається натуральним і позначається ln b.
- Логарифмування - дія знаходження логарифма числа або виразу .
- Перетворення, за допомогою якого за даним логарифмом числа (виразу) визначають саме число (вираз), називають потенціюванням
- Усна вправа «Розминка» Обчислити:
lg0,01 = - 2; log2 1=0; log9 9 = 1; log5![]() = - 1; log3 81= 4; log618+ log62 =2;
= - 1; log3 81= 4; log618+ log62 =2; ![]() = 3; lg120 - lg12 = 1; log31+ 6=6;
= 3; lg120 - lg12 = 1; log31+ 6=6; ![]() = 4.
= 4.
3. Усна вправа «Встановіть відповідність»
(Учням потрібно встановити відповідність між властивостями логарифмів)

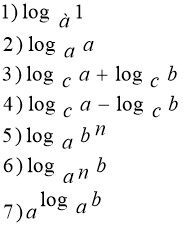
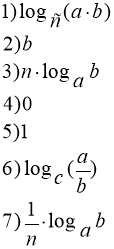
Відповідь: 1 – 4, 2 – 5, 3 – 1, 4 – 6, 5 – 3, 6 – 7, 7 – 2.
- Вивчення нового матеріалу.
План :
- Означення логарифмічного рівняння. Найпростіше логарифмічне рівняння.
- Способи розв’язування логарифмічних рівнянь:
- за означенням логарифма;
- метод потенціювання;
- за властивостями логарифмів;
- метод введення нової змінної;
- метод зведення до однієї і тієї ж основи;
- метод логарифмування;
- графічний метод.
Означення: Логарифмічними називають рівняння, які містять змінну під знаком логарифма. Наприклад: log5 x = 2; lg х = 1 + lg2x, log3(x + 3) = 9 і т. д.
Розв'язати логарифмічне рівняння — це означає знайти всі його корені або довести, що рівняння коренів не має.
Найпростіше логарифмічне рівняння – це рівняння виду log a х = b, де а > 0, а ≠ 1, х > 0. Під час розв’язування логарифмічних рівнянь обов’язково треба знаходити область допустимих значень (ОДЗ) рівняння або робити перевірку знайдених коренів.
Способи розв’язування логарифмічних рівнянь:
I спосіб. За означенням логарифма.
Таким способом найчастіше розв’язуються найпростіші логарифмічні рівняння. За означенням логарифма маємо: якщо log a х = b, де а > 0, а ≠ 1, х > 0, то х = аb . Також цей спосіб застосовують і для розв’язування рівнянь виду log a f(х) = b, де а > 0, а ≠ 1, f(х) > 0. ( Їх також відносять до найпростіших логарифмічних рівнянь.) Для таких рівнянь f(х)= аb.
Приклад 1. Розв’язати рівняння log2 x = 3.
Розв'язання: Область допустимих значень рівняння: x > 0. За означенням логарифма маємо: x = 23, x = 8. 8 ![]() ОДЗ.
ОДЗ.
Відповідь: x = 8.
Приклад 2. Розв'яжіть рівняння log3 (2x + 1) = 2.
Розв'язання: За означенням логарифма маємо: 2х + 1 = 32, 2х = 8, х = 4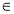 ОДЗ.
ОДЗ.
Відповідь: 4.
Коментар: В цьому прикладі 2х +1 > 0, так як 32> 0, тому зайвих коренів з’явитись не може і перевірку не потрібно робити. Умову 2х+1 > 0 в цьому прикладі виписувати не потрібно.
Приклад 3. Розв'яжіть рівняння logх-1 (5- х ) = 1.
Розв'язання: Знайдемо ОДЗ рівняння: 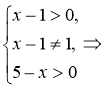
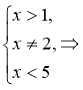
![]()
За означенням логарифма маємо: 5 – х = х – 1; 2х = 6; х =3 є ОДЗ.
Відповідь: 3.
IІ спосіб. Метод потенціювання.
Розглянемо логарифмічне рівняння виду logaf(x)=logag(x), де a > 0, a ![]() 1.
1.
Яку особливість ви помітили? (Основи логарифмів однакові і значення логарифмів двох виразів рівні) Який висновок можна зробити? (Значення виразів, які стоять під знаком логарифма, також рівні)
Перехід від рівняння loga f(x) = loga g(x) до рівняння f(x) = g(x) називається потенціюванням. Однак, при такому переході може порушитись рівносильність рівнянь. Тому при застосуванні цього методу обов’язково треба знаходити ОДЗ рівняння або робити перевірку коренів. Розв’язування таких рівнянь зводиться до розв’язування системи: 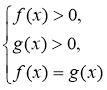 .
.
Однак, дана система містить зайву умову. Як ви вважаєте, чому? Дійсно, одну з нерівностей можна не розглядати.
Отже, розв’язування рівнянь виду loga f(x) = loga g(x) методом потенціювання рівносильне розв’язуванню системи:
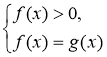 або
або 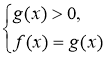 .
.
Іноді зручно область визначення знаходити окремо, і вже після розв’язання рівняння перевірити, належать його корені до області визначення чи ні.
Приклад 4. Розв’язати рівняння log3 (x2 – 3x – 5) = log3 (7 – 2x).
Розв'язання: Знайдемо ОДЗ рівняння: ![]() . Пропотенціюємо дане рівняння, отримаємо: х2 – 3х – 5 = 7 – 2х, х2 – х – 12 = 0, звідки за теоремою Вієта х1 = –3, х2 = 4. Число 4 не належить до ОДЗ.
. Пропотенціюємо дане рівняння, отримаємо: х2 – 3х – 5 = 7 – 2х, х2 – х – 12 = 0, звідки за теоремою Вієта х1 = –3, х2 = 4. Число 4 не належить до ОДЗ.
Відповідь: x = –3.
ІIІ спосіб. Розв’язування логарифмічних рівнянь за властивостями логарифмів.
Приклад 5. Розв'яжіть рівняння log5(x – 1) + log5(x – 2) = log5(x + 2).
Розв'язання: Чи можна це рівняння розв’язати за означенням логарифма? (Ні, тому що воно не є найпростішим)? Чи можна застосувати метод потенціювання до цього рівняння? Чому? (Ні, тому що воно не відповідає виду loga f(x) = loga g(x)) А чи можна звести таке рівняння до цього виду? (Так, застосувавши властивість логарифмів) Яку саме? (Логарифм добутку двох додатних чисел дорівнює сумі логарифмів цих чисел)
Але, перш ніж перетворювати рівняння, знайдемо ОДЗ рівняння:
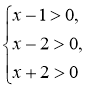 x
x ![]() (2;
(2; ![]() ).
).
Застосуємо властивість логарифмів, отримаємо: log5((x – 1)(х – 2)) = log5(x + 2);
Пропотенціюємо дану рівність і одержимо: (х – 1)(х – 2) = х + 2; x2 – 2х – х + 2 = х + 2; x2 – 4х = 0; х(х – 4) = 0; х = 0 або х = 4. 0 не належить до ОДЗ.
Відповідь: 4.
ІV спосіб. Метод введення нової змінної.
Приклад 6. Розв'яжіть рівняння log![]() х – 3log2 x – 4 =0.
х – 3log2 x – 4 =0.
Яким із вже відомих нам способів можна розв’язати дане рівняння? (Жодним) Що ви помічаєте? (Що це квадратне рівняння відносно log2x) Що ви пропонуєте зробити? (Ввести нову зміну)
Розв'язання: Знайдемо ОДЗ рівняння: х > 0.
Позначимо log2 x через t. Дане рівняння набуде вигляду: t2 – 3t – 4 =0. За теоремою Вієта, знайдемо корені рівняння: t1 = 4; t2 = -1. Повертаємося до заміни: log2 x = 4, log2 x = - 1 . Отримали найпростіші логарифмічні рівняння. Розв’язавши їх, одержимо:
x = 24 ![]() x = 16 та x = 2-1
x = 16 та x = 2-1 ![]() x =
x = ![]() .
.
Відповідь: 16; ![]() .
.
Оскільки після заміни змінної отримуємо алгебраїчне рівняння, то цей спосіб називають ще способом зведення логарифмічного рівняння до алгебраїчного.
V спосіб. Метод зведення до однієї і тієї ж основи.
Приклад 7. Розв'яжіть рівняння ![]() .
.
Розв'язання: Знайдемо ОДЗ рівняння: х > 0. Перейдемо до однієї основи 3:
![]() або
або ![]() ,
, ![]() ,
, ![]() . Отримали найпростіше логарифмічне рівняння, розв’язавши яке отримаємо корінь рівняння:
. Отримали найпростіше логарифмічне рівняння, розв’язавши яке отримаємо корінь рівняння: ![]() .
.
Відповідь: 9.
VІ спосіб. Метод логарифмування.
Приклад 8. Розв'яжіть рівняння х lgx = 100х.
Таке рівняння називають показниково-логарифмічним або показниково-степеневим, оскільки воно містить невідоме в основі степеня, і в показнику степеня. Як правило, такі рівняння розв’язують логарифмуванням обох частин рівняння.
Розв'язання: ОДЗ рівняння: х > 0.
Прологарифмуємо обидві частини рівності, одержимо: lgx lgx = lg(100x);
lgx lgx = lg 100 + lgx; lg2x – lg x – 2 = 0.
Замінимо lg х = t. Рівняння прийме вигляд: t2 – t – 2 = 0; t1 = 2, t2 = -1.
Тоді: 1) lg х = 2; х = 102; х = 100.
2) lg x = -1; x = 10-1; x = 0,1.
Відповідь: 100; 0,1.
VІІ спосіб. Графічний метод.
Приклад 9. Розв'яжіть графічно рівняння : log2x= 3 – x.
У чому полягає графічний спосіб розв’язування рівнянь? Як ви пропонуєте розв’язати дане рівняння?
(Побудувати графіки двох функцій f(x) = log2x і g(x) = 3 – x та знайти абсциси точок перетину графіків). Розглянемо розв’язання рівняння на слайді.
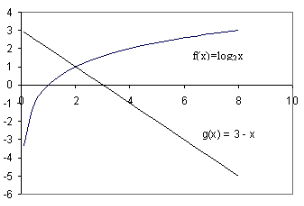
Відповідь: 2.
- Закріплення вивченого матеріалу.
Завдання № 1. Оберіть спосіб розв’язування рівнянь.
|
|
Завдання № 2. Вкажіть область допустимих значень (ОДЗ) рівняння. (Резерв)
![]()
![]()
![]()
![]()
![]()
А тепер повернімось до малюнків, які ви побачили на початку заняття. Виявляється, ряд явищ природи допомагає описати саме логарифмічна залежність. Математики, складаючи математичну модель того чи іншого явища, досить часто звертаються саме до логарифмічної функції. Одним з найбільш наглядним прикладом є логарифмічна спіраль. Докладніше про логарифмічну спіраль нам розкаже Іванова Валерія. (Доповідь учениці)
- Підсумок заняття.
Отже, ми ще раз переконалися, що знання з математики допомагають людині жити в сучасному світі, пізнавати всі його дива і таємниці. Саме математика - знаряддя, за допомогою якого людина пізнає і підкорює собі навколишній світ.
Отож, давайте пригадаємо, яку тему ми сьогодні вивчали на уроці?
Які рівняння називаються логарифмічними?
Чи є універсальний спосіб розв’язування логарифмічних рівнянь?
Які способи розв’язування логарифмічних рівнянь вам відомі?
Як можна встановити, чи є знайдене значення коренем рівняння?
Хочу закінчити заняття словами американського математика Моріса Клайна:
«Музика може піднімати або умиротворяти душу,
Живопис - радувати око,
Поезія - пробуджувати почуття,
Філософія - задовольняти потреби розуму,
Інженерія - удосконалювати матеріальну сторону життя людей,
А математика здатна досягти всіх цих цілей».
- Домашнє завдання.
Шкіль М.І. Алгебра і початки аналізу 10-11 кл. Розділ V, §3.
Мерзляк А. Г. Алгебра 11 кл. § 2, п.21.
Мерзляк А. Г. Алгебра 11 кл: збірник задач і контрольних робіт № 88 (1, 2, 3, 6, 7), № 89 (1, 2), № 90 (1).
Література:
- Афанасьєва О. М., Бродський Я. С., Павлов О. Л., Сліпенко А. К. Математика. 11 клас: Підручник для загальноосвітніх навчальних закладів. Рівень стандарту. – Тернопіль: Навчальна книга. – Богдан, 2011. – 480 с.
- Мерзляк А. Г. Алгебра 11 кл: збірник задач і контрольних робіт /А. Г. Мерзляк, В. Б. Полонський , Ю. М. Рабінович, М. С. Якір. – Х.: Гімназія, 2012.
- Мерзляк А. Г. Алгебра 11 кл: підруч. для загальноосвіт. навальн. закладів: академ.рівень, проф. рівень /А. Г. Мерзляк, В. Б. Полонський , Ю. М. Рабінович, М. С. Якір. – Х.: Гімназія, 2011. – 431 с. : іл.
- Шкіль М.І. Алгебра і початки аналізу 10-11 кл. [Текст] : підручник / М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук – К. : Зодіак - ЕКО, 2002.
1


про публікацію авторської розробки
Додати розробку

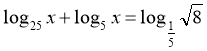 ;
;