Конспект уроку з алгебри в 9 класі на тему "Найпростіші перетворення графіків функції"

КРИНИЧНЕНСЬКА   ЗАГАЛЬНООСВІТНЯ  ШКОЛА  І-ІІІ  СТУПЕНІВ

 

 

 

 

 

 

 

 

 

ВІДКРИТИЙ   УРОК 

 

 

 

РОЗРОБКА  УРОКУ  З  АЛГЕБРИ 

 

9  клас

 

ТЕМА:   НАЙПРСТІШІ  ПЕРЕТВОРЕННЯ  ГРАФІКІВ  ФУНКЦІЙ

 

 

 

 

 

 

 

 

вчителя  математики,

вищої  категорії,

«старший  учитель»

МАКСИМОВОЇ  СОФІЇ  МИХ.

 

 

 

 

КРИНИЧНЕ,  2020 р.

Урок математики (алгебри) в 9 класі     

 

29.11.2020р.

 

  Вчитель Максимова С.М.

 

Тема уроку: Найпростіші перетворення графіків функцій.

 

Цілі уроку:

• Дидактична: сформувати в учнів розуміння змісту поняття «перетворен­ня графіка функції», а також факту, що певне перетворення форму­ли, що задає функцію, спричиняє перетворення графіка, і навпаки. Сформувати знання учнів про основні види геометричних перетво­рень графіків функцій (на інтуїтивному рівні) та про формули функ­цій, що задаються цими перетвореннями. Сформувати первинні вміння «читати» графіки функцій (тобто за готовими графіками за­давати функцію), а також виконувати побудову графіка функції, ви­конуючи перетворення, що задані функцією.
• Розвивальна: розвивати логічне мислення, допитливість учнів; формувати вміння застосовувати набуті знання.
• Виховна: виховувати почуття любові до рідної Землі, прагнення до самоосвітньої діяльності.

 

Тип уроку: урок засвоєння нових знань.

 

План уроку

1. Вступне слово вчителя, повідомлення теми, мети й завдань уроку
2. Актуалізація опорних  знань.
3. Засвоєння нових знань.
4. Закріплення нового матеріалу.
5. Підведення підсумків уроку.
6. Домашнє завдання

Конспект уроку

 

ХІД УРОКУ:

І. Організаційна частина.

1. Вступне слово вчителя.

Привітання та психологічний налаштунок на урок.)

Добрий день, учні! Сьогодні  в нас незвичайний  урок – відкритий  урок  з

алгебри  для  вчителів  математики  нашого  району.  Привітайтеся,  будь  ласка.

 Урок я хочу почати зі слів американського  математика  Роберта  Вінера,

засновника  кібернетики.

                                                      Найвище  призначення  математики  

                                               полягає в тому,  щоб  знаходити 

                                              потаємний  порядок  у  хаосі,  який  нас 

                                               оточує.

Роберт  Вінер

І  відразу  хочу  вам  запропонувати  переконатися  в  цьому,  подивившись

відео ролік  про  функцій  навколо  нас. (Слайд)

 

Чи  сподобалося  вам?  Мабуть,  ви  ще  раз  переконалися  в  тому,  що  вивчення  функцій  та  їх  властивостей  є  дуже  важливою  та  необхідною  темою.  Тому  ми  з  вами  продовжимо  вивчення  теми  «Функції, їх  графіки  та  властивості».

Перш  ніж  перейти  до  наступного  етапу  нашого  уроку  зверніть,  будь  ласка,  увагу  на   аркуші  на  вашому  столі.

У кожного з вас на парті є карта самоконтролю. Заповніть її будь-ласка. Ви бачите 7 видів завдань, за виконання яких ви будете отримувати певну кількість балів.

Карта самоконтролю учня (учениці) 9–Б класу

 

________________________________________________ група  ____

Кількість балів	Оцінка
29	12
27-28	11
25-26	10
22-24	9
19-21	8
17-18	7
14-16	6
11-13	5
9-10	4
5-8	3
3-4	2
1-2	1

 

Кількість балів за виконання завдань

 

1. Самостійна робота №1      ____________
2. Знайди  пару                     ____________
3.  Робота  на проектом        _____________
4. Усне опитування             _____________
5. Відповідність                   _____________
6. Письмова  робота ПР       _____________
7. Визначити  функцію       ____________

 

Загальна кількість балів ____________

 

                Оцінка ____________________

 

Отже всім бажаю успіху і вдачі. Будьте на уроці:  У – успішними,

 С – спокійними,    П – працьовитими,    І – ініціативними, Х – хоробрими.

 Перевірка домашнього завдання.

        Щоб   перейти  до  роботи  над  темою  нашого  уроку,  перевіримо, як  ви  впоралися  із  виконання  д/з.

Перше завдання – самостійна робота №1, яке перевіряє рівень вашої підготовки до цього уроку. (Час виконання роботи  1  хвилина.) (Робота проводиться  в  групах за  різним рівнем  підготовки).

 

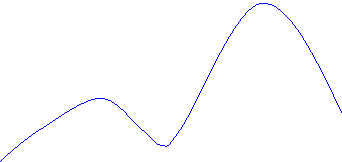
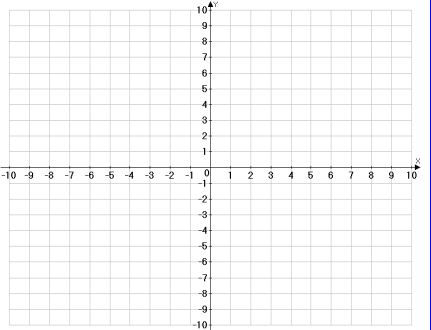
На малюнку  зображено  графік  функції  y=f(x).  Знайти:

1. Область  визначення  функції.                                                   4 гр      
2. Область  значень  функції.                                                         4 гр       
3. Нулі  функції.                                                                             1 гр    
4. Проміжки  на  яких  функція  зростає.                                      2 гр    
5. Проміжки  на  яких  функція  спадає.                                       3 гр
6. Проміжки  на  яких  функція  набуває  додатні  значення.       3 гр
7. Проміжки  на  яких  функція  набуває  від’ємні   значення.      2 гр 
8. Найменше найбільше значення  функції.                                  1 гр
9. Найбільше значення  функції.                                                    4 гр
10.                     Значення  функції,  коли  х=0.                                          3 гр

 

( за кожне  завдання  1 бал )

 

(Після закінчення виконання роботи перевірка  відповідей  й  відкриття  поля з  табличок з  відповідями,  де зашифрований  вираз,  або  прізвище  вченого-математика, або  прізвища  вчених.)

 

8	(- 4; -1) U ( 4; 8)	[ -2; 8 ]	(- 9; -4) U ( -1; 4)
-7; -2; 0	[ -9; 8 ]	( - 7; - 2) U ( 0; 8)
0	( -9; - 7) U ( -2; 0)	2

 

(Відкривається   табличка  з  прізвищами  вчених-математиків,  які  мали  відношення  до  вивчення  теми  про  функцію  та  досліджували  функції)

 

П’эр Ферма	Ейлер	Лобачевський	Лейбніц
Рене  Декарт	Д’Аламбер	Діріхле	Бернуллі
Ньютон	Дедекинд	Пеано	Больцано

 

(Відповіді  учнів  з  історії  про даних  вчених.)

• П’єр Ферма і  Рене  Декарт – у  першій  половині  XVII  століття  заклали  основи  для  виникнення  поняття  функції.  В  своїх  роботах  вони  досліджували  зміну  ординати  точки  в  залежності  від  зміни  її  абсциси.
• Ісаак  Ньютон – англійський  учений – під   функцією  мав  на  увазі  величину,  яка  змінюється  з  плином  часу.
• Ейлер  (1751р)   і  Д’Аламбер – сформували  більш  загальний  вигляд  функції  як  залежність  однієї  змінної  величини  від  іншої,  в  якому  це  поняття  не  завжди  було  пов’язане  зі  способом  задання  функції.
• Лобачевський (1834р)  і  Діріхле(1837р) – нарешті  висувають  означення  функції  вже  практично  в  сучасному  вигляді,  але  тільки  для  числових  функцій.
• Дедекинд (1887р)  і  Пеано (1911р) – після  з’явлення  теорії  множин  сформулювали  сучасне  універсальне  означення  функції.
• Лейбниц – першим  ввів  термін  «функція».  Він  і  його  учень  Бернуллі  під  функцією  мали  на  увазі  формулу,  яка  пов’язує  одну  змінну  з  іншої,  тобто  прирівнювали  функцію  до  одного  зі  способів  її  задання.

З  ім’ям  Лейбніц  у  науці  пов’язано  багато  відкриттів  і  гіпотез,  які  згодом  отримали  визнанне.  Він  займався  хімією  і  геологією,  сконсруював  повітряний  двигун  для  насосів,  які  викачують  воду  із  шахт.   В  механіці  йому  належіть  поняття  «живі  сили»,  в  геології – думка,  що  Земля  має  історію.   Лейбніц  висловив  правильне  твердження  про  походження  копалин  останків  тварин  і  рослин,  відстоював  дуже  важливу  для  біологів  думку  про  еволюцію.   Він  створив  власну  наукову  школу  математиків.  Першим  порушив  традиції  писати  наукові  роботи  тільки  латинською  мовою.

• Больцано – чеський  математик,  філософ  та  логік. На  жаль  за  життя  він  надрукував  тільки  5  невеликих  математичних  творів.  Велика  математична  праця  «Вчення  про  функції»,  яка  була  написана  у  1830  році,  побачила  світ  тільки  через  100  років.  Саме  Больцано  належіть  фраза: «Формула  іноді  здається  більш  мудрою,  ніж  людина,  яка  її  придумала».

 

Сьогодні  ми  продовжимо  з  вами  дослідження  функцій.  Перевіривши  домашнє  завдання,  ви  ще  раз  переконалися  у  тому,  що  дослідження функції за готовим графіком є більш простим, ніж за формулою (підтвердженням цієї думки можуть стати результати перевірки тестових завдань з домашнього завдання).

 В ряді випадків для розв’язування задач буває необхідно побудувати графік функції, яка не є елементарною   ( наводимо  приклади:   y = - √x,  y = x² + 3,            y = (x – 5)²,      та  інші).

Отже, формулюється питання: чи існують засоби за допомогою яких можна побудувати графік деякої функції, використовуючи вміння будувати графіки елементарних функцій (лінійної, оберненої пропорційності, квадратичної функції та функції ).                   

Якщо існують, то як ними користуватися?

Зрозуміло, що пошук відповіді на поставлене питання і є метою нашого уроку.

Запишіть,  будь ласка,  число,  класна  робота,  тему  уроку « Найпростіші  перетворення  графіків  функцій».

 Сьогодні на уроці ми познайомимося з  основними видами  геометричних    перетворень  графіків  елементарних  функцій   та  формулами  функцій,  що  задаються  цими  перетвореннями,  навчимося  «читати»  графіки  функцій (тобто  за  готовими  графіками  задавати  функцію),  а  також  виконувати  побудову  графіка  функції,  виконуючи  перетворення,  що  задані  функцією.

 

 

 

План вивчення нового матеріалу:

1. Уявлення про перетворення графіків функцій.
2. Побудова графіків із застосуванням симетрії відносно осі абсцис.
3. Побудова графіків паралельним перенесенням уздовж осі ординат .
4. Побудова графіків паралельним перенесенням уздовж осі  абсцис.

 

Але спочатку повторимо деякі теоретичні положення (усно).

2. Актуалізація  знань. 

 

  Знайдіть  пару (з’єднати  стрілками,  1 бал  за  кожне правильне завдання) 1 хвилина

 

Формула	Графік	Відмітка  про  виконання
y = x²	у         х
y = k x	У            х х
y = k x + b	у           х
y = √ x	у          х
k y = —      x	у         х

 

3. Засвоєння   нових  знань.

      Зараз з вашою допомогою ми дослідимо нові перетворення графіків функцій. Кожна група учнів отримала  домашнє завдання на побудову графіків різних  функцій  за  допомогою  способів, які ви  знаєте  з  попередніх  років. Тому  протягом 5-7 хвилин ми  з  вами  послухаємо  представників  груп, які  будуть  презентувати  свої  проекти.

      (Презентація проектів. Під час презентації учні заповнюють таблицю перетворень графіків функцій у зошитах, виставляють оцінку за роботу.)

 

3  група
y = x²;  y = - x²;  y = √x ; y = - √x	x -3 -2 -1 0 1 2 3 y 9 4 1 0 1 4 9   x -3 -2 -1 0 1 2 3 y -9 -4 -1 0 -1 -4 -9   x 0 0,25 1 2,25 4 6,25 9 y 0 0,5 1 1,5 2 2,5 3   x 0 0,25 1 2,25 4 6,25 9 y 0 -0,5 -1 -1,5 -2 -2,5 -3

 

1. Слайд з  опорним  конспектом.

 

 

Слайд з графіком. Приклад.

 

1  група	x -3 -2 -1 0 1 2 3 y 9 4 1 0 1 4 9   x -3 -2 -1 0 1 2 3 y 12 7 4 3 4 7 12   x -3 -2 -1 0 1 2 3 y 4 -1 -4 -5 -4 -1 4
y = x² ;  y = x² + 3;  y = x² - 5;

 

   2. Слайд з  опорним  конспектом

 

Слайд з графіком.  Приклад.

 

2  група	x -3 -2 -1 0 1 2 3 y 9 4 1 0 1 4 9   x -7 -6 -5 -4 -3 -2 -1 y 9 4 1 0 1 4 9   x 2 3 4 5 6 7 8 y 9 4 1 0 1 4 9
y = x²;  y = (x + 4)² ;  y = (x – 5)²;

 

3.Слайд з  опорним  конспектом

 

Слайд з графіком.  Приклад.

 

4  група	x -3 -2 -1 0 1 2 3 y 9 4 1 0 1 4 9   x -3 -2 -1 0 1 2 3 y -9 -4 -1 0 -1 -4 -9   x 0 1 2 3 4 5 6 y -9 -4 -1 0 -1 -4 -9   x 0 1 2 3 4 5 6 y -4 1 4 5 4 1 -4
y = x²;  y = - x²;  y = - (x - 3)²;  y= - (x - 3)²+ 5;

 

Слайд з графіком  з  послідовним  перетворенням.  Приклад.

( За  проект  група  отримує  5 балів )

4. Закріплення  нового  матеріалу.

 

1.Виконання усних вправ у групах. ( на обміркування  і  відповіді  2-3 хвилини)

1  група

За допомогою  яких  перетворень  можна  отримати  з  графіка  функції  у = х2  графіки  функцій: у=х²-1;       2)  у=(х+1)².

Перенесенням графіка функції у=х2 :   а) на  1 одиницю  вверх; б) на  1  одиницю  вправо; в) на  1 одиницю  вниз; г) на  1 одиницю  вліво.

 

2  група

Графік функції у = х2 перенесли вправо на 2 одиниці. Позначте функцію, графік якої отримали. Графік функції у = х2 перенесли вниз на 2 одиниці. Позначте функцію, графік якої отримали. Графік функції у = х2 перенесли  вверх   на 2 одиниці  і  вліво  на  2  одиниці. Позначте функцію, графік якої отримали.

А) у = х2 + 2                                                              Б) у = х2 – 2   В) у = (х + 2)2                                                   Г) у = (х – 2)2   Д) у = (х + 2)2 + 2    Г) у = (х – 2)2 – 2

 

3  група

Графік функції  можна отримати із графіка функції , якщо виконати паралельне перенесення _____________. Графік функції  можна отримати із графіка функції , якщо виконати паралельне перенесення ______________.

 

4  група

Запишіть формули функцій, графіки яких зображені на відповідних рисунках:

( Перевірку виконання письмової роботи здійснюють за зразком  взаємоперевіркою у групах.  За  кожне  правильне  завдання  1 бал).

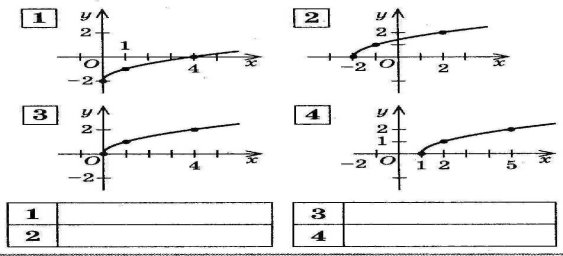
2. Встановіть відповідність між графіком функції і формулою. 

( на  виконання і  відповіді   1-2   хвилини )

 

 

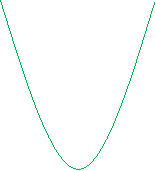
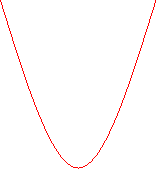
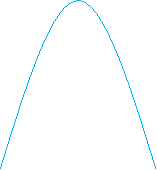
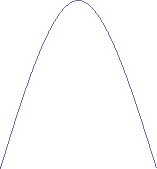
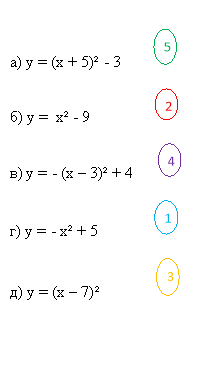
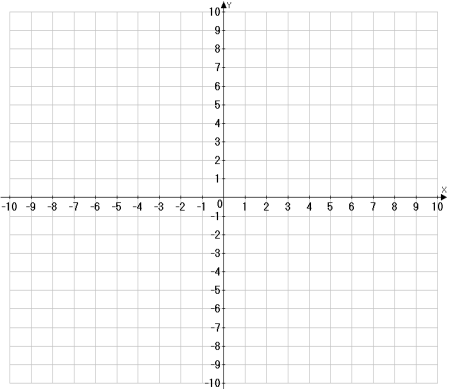
( За  кожне  правильне  завдання  1  бал )

 

 

 

 

3. Виконання  письмових  вправ  у  групах.  Практична  робота.   

( на  виконання  вправи  3-5 хвилин )

 

Група	Функція	графік
1	y=(x-3)2
2
3	y=(x+3)2-7
4

 

 ( Перевірка  виконується  за  зразком на  дошці )

( За   правильне   виконання  завдання  3 бали.)

 

 

 

 

 

 

 

 

4. Визначити, графік якої функції побудовано.  Запишіть  формулу.

 ( на  виконання і відповіді   2-3  хвилини )

 

1 гр 2гр

    y = x² - 4                                                          y = (x –6)² + 3

                                                        

3гр 4гр

            y = (x +2)² - 4                                               y = - (x + 3)² + 5

 

4гр                      

 

                  y = - (x – 4)² + 1

 

( За  кожне  правильне  завдання  2  бали )

5. Підведення  підсумків  уроку. 

 

      Ми з вами  дослідили  перетворення графіків функцій. Пригадаємо їх ( вчитель показує функцію на плакатах, учні називають які перетворення необхідно  виконати ).

1.  Побудова графіків із застосуванням симетрії відносно осі абсцис.
2. Побудова графіків паралельним перенесенням уздовж осі ординат .
3. Побудова графіків паралельним перенесенням уздовж осі  абсцис.

 

 Чому ви навчилися на сьогоднішньому уроці?

   (…визначати  функції  за  графіком,  будувати  графіки  функцій  за  формулами)

 Яку оцінку ви б поставили собі за урок? (Відповідь запишіть на  полях  зошиту.)

 (Занесення результату до карти самоконтролю.)

         Просумуйте отримані бали і згідно таблиці отримайте оцінку.

 Поміркуємо разом:

 Чи збіглися   ваші отримані результати з власною оцінкою? Що  треба  зробити,  щоб  очікувані  результати  відповідали  отриманим?

 (Після уроку учні здають карти самоконтролю вчителю для виставлення оцінки до журналу. Вчитель повідомляє, що оцінки менші семи балів виставлятися не будуть і учень отримує можливість допрацювати матеріал і покращити оцінку.)

 

6. Домашнє  завдання

            На наступному уроці  ми продовжимо роботу над темою. Щоб закріпити отримані знання на уроці вдома виконайте завдання за  рівнями  у  групах. 

§2  п.10,    

група	1 гр	2 гр	3 гр	4 гр
№  вправи	303, 305, 308	317		312(4-6)
Творче  завдання	Придумати  дві  неелементарні функції  та  побудувати  їх  графіки.
	Бажаючим  пропонується  підготувати  презентацію  про  те,  де  ми  зустрічаємося  з  графіками  функцій:  у  школі,  у  побуті,  на  виробництві,  у  житті.

 

7. Рефлексія.

    Діти  на  початку  уроку  я  вам  запропонувала  бути:

Успішними,  Спокійними,  Працьовитими,  Ініціативними, Хоробрими.

   Якими   ви  почували  себе  на  сьогоднішньому  уроці?  Піднміть  руку  хто  був  успішним,  спокійним,  працьовитим, ініціативним,  хоробрим.

           Мені приємно бачити ваші усмішки. Бажаю вам зберігати гарний настрій протягом тривалого часу. На цьому урок закінчено.  Дякую  за  співпрацю.