Презентація до уроку алгебри в 9 класі на тему "Найпростіші перетворення графіків функції"
Про матеріал
Пропоную презентацію до уроку алгебри в 9 класі на тему "Найпростіші перетворення графіків функції" з використанням анімації. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
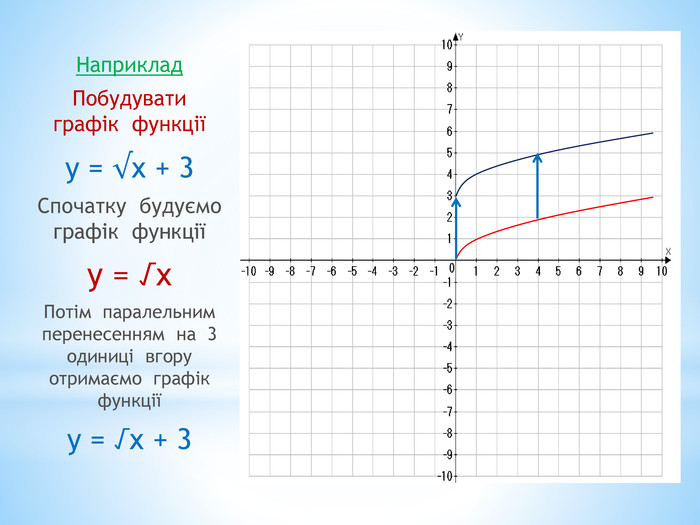
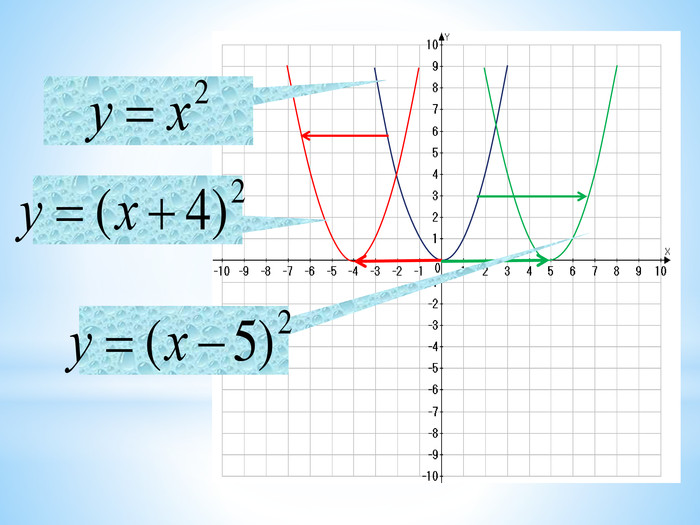
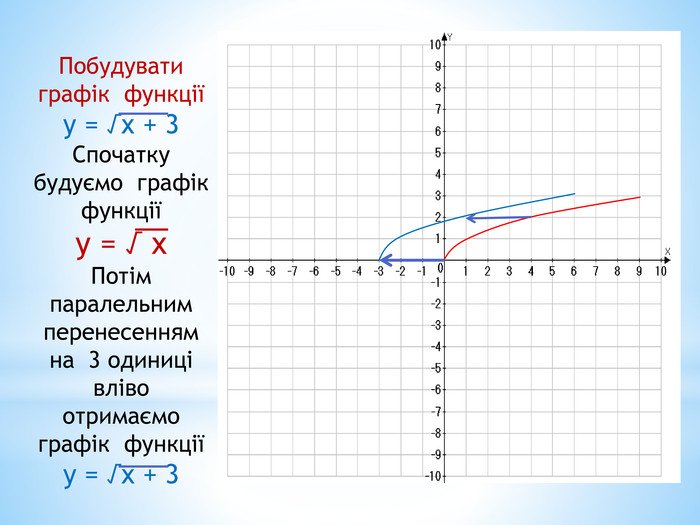
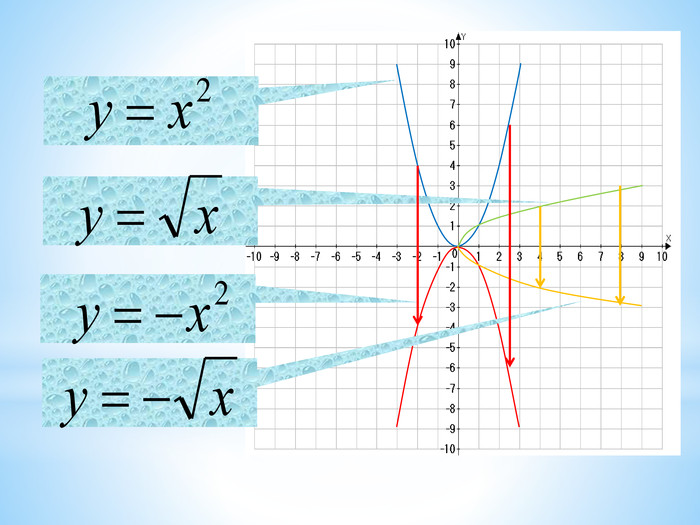
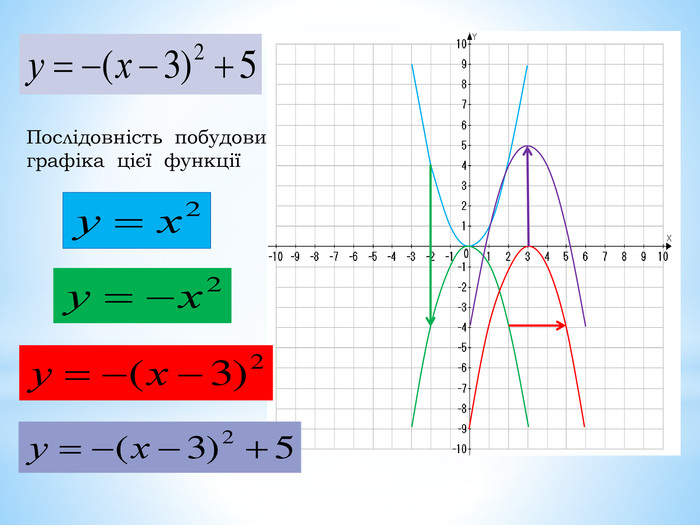
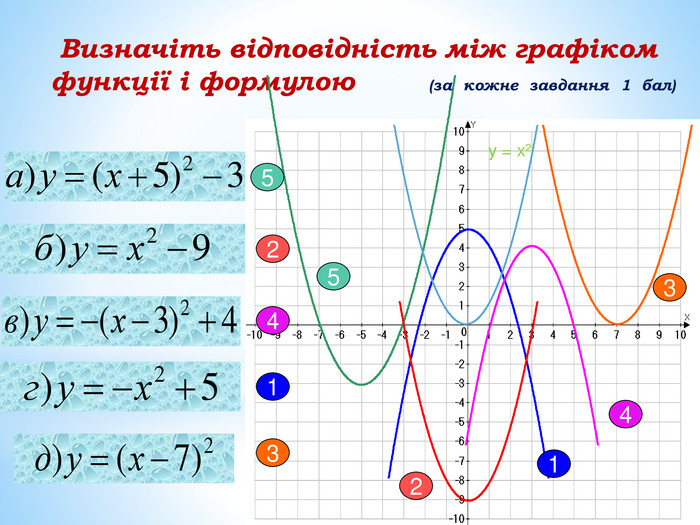
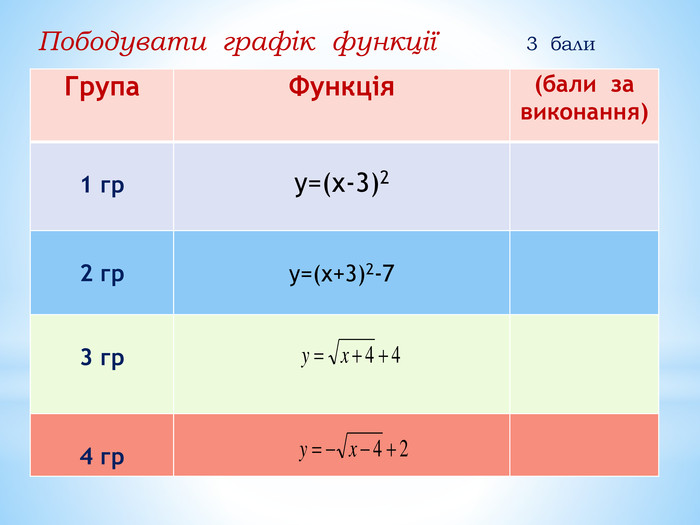
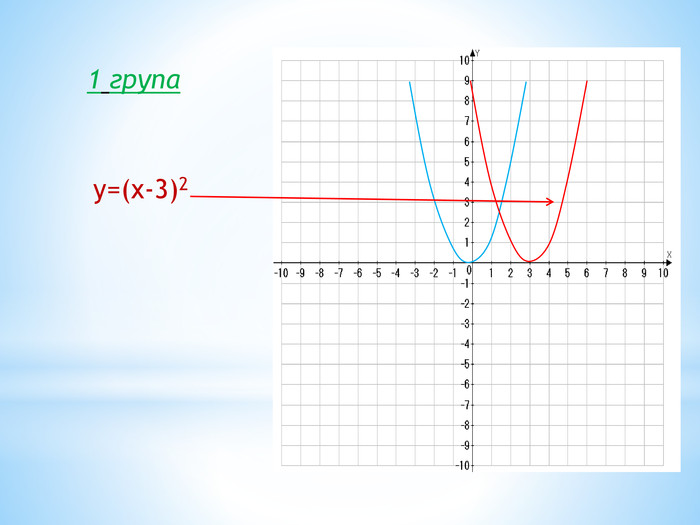
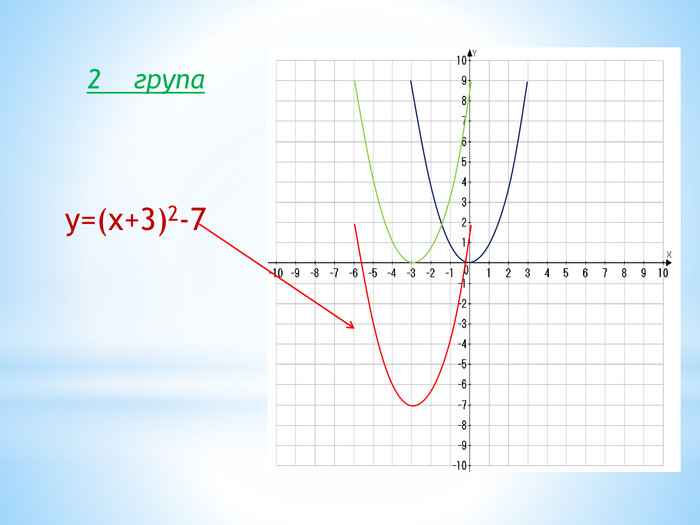
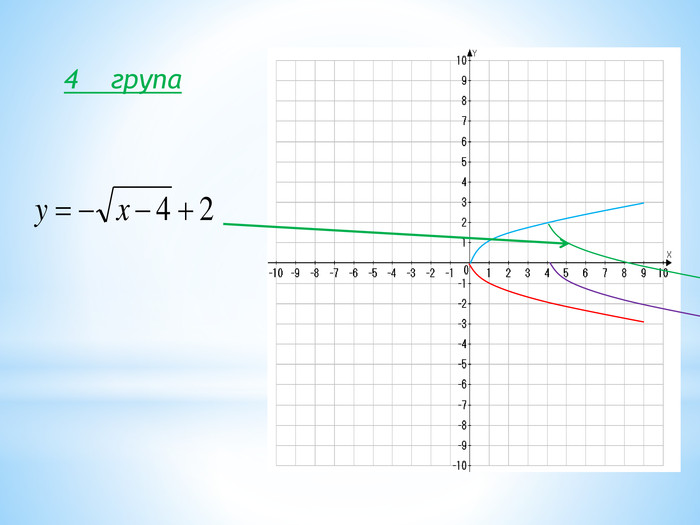
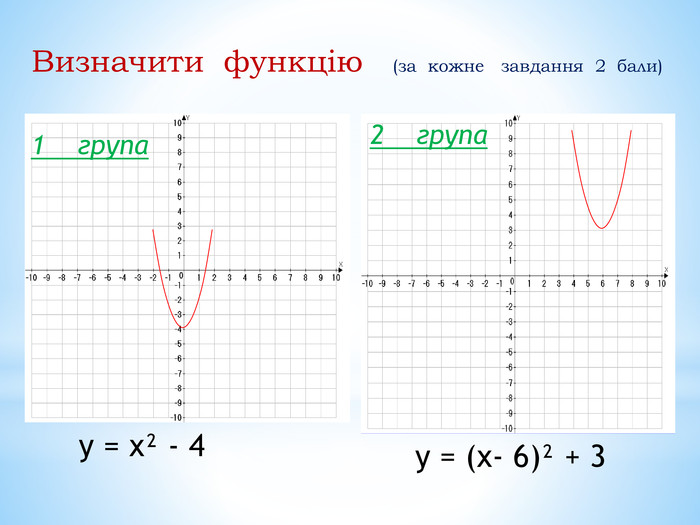
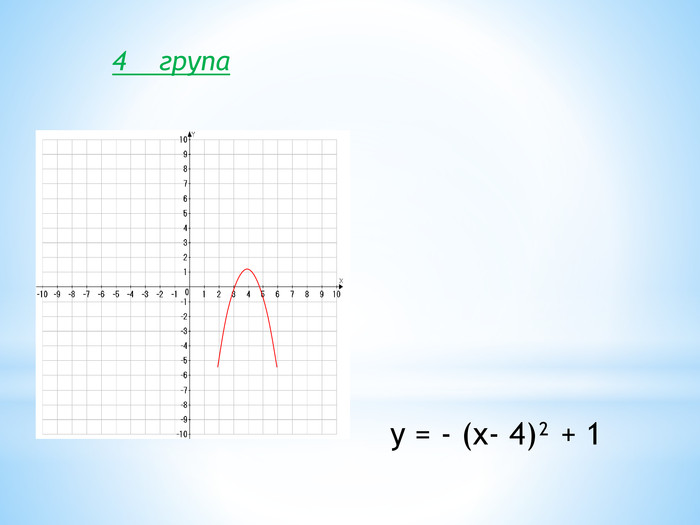
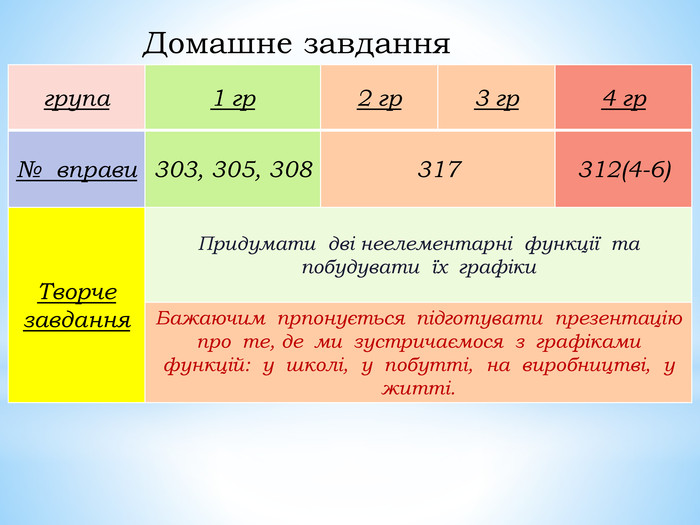
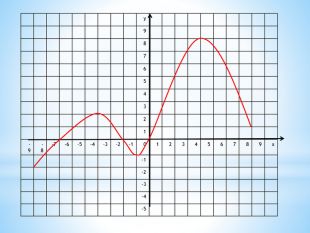
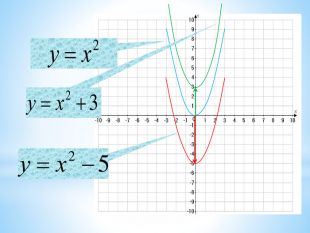
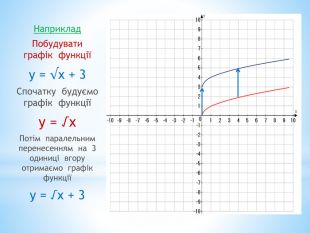
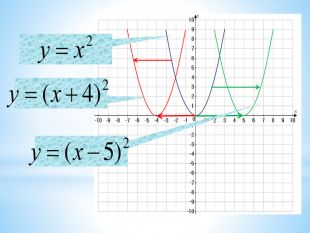
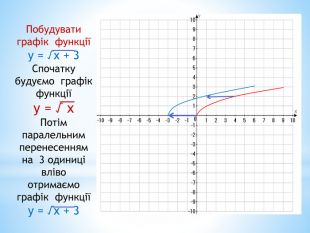
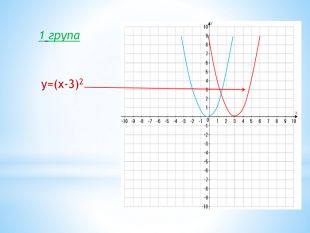
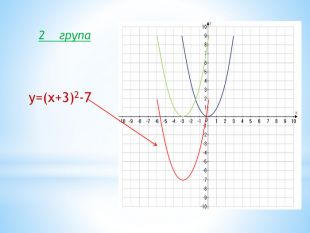
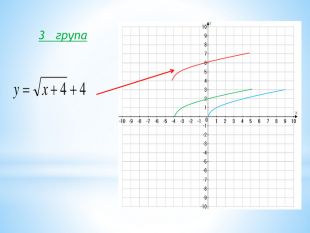
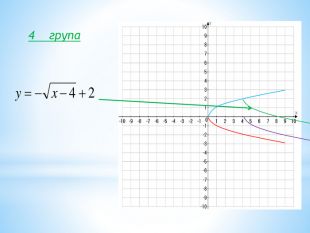
10. Як побудувати графіки функцій y = f (x) + b і y = f (x + a), якщо відомо графік функції y = f (x) Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
































-

Данилець Вікторія
17.11.2024 в 18:54
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сальник Ольга Іванівна
04.12.2023 в 19:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тиртишна Олена Іванівна
30.11.2022 в 19:58
Дякую! Гарна розробка.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Погорелова Лариса Захарівна
28.11.2022 в 14:03
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кобринчук Антоніна Борисівна
03.11.2022 в 10:29
Дякую.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Строкіна Лідія Миколаївна
21.10.2022 в 11:34
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Добреля Тетяна Степанівна
07.09.2022 в 18:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Єнікеєва Тетяна Степанівна
04.05.2022 в 15:31
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Перепелиця Тетяна Іванівна
29.11.2021 в 19:23
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Корольчук Олена Іванівна
14.11.2021 в 21:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Корольчук Олена Іванівна
14.11.2021 в 21:58
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Anatoliivna Olena
28.04.2021 в 11:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 9 відгуків