Конспект уроку з геометрії у 8 класі "Теорема Піфагора"
Конспект уроку з теми: теорема Піфагора.
Мета :розширити пізнання про життя великого математика і про знамениту теорему, навчити учнів застосовувати теорему під час розв'язування задач на практиці і в повсякденному житті; виховувати в учнів відповідальне ставлення до навчання; бажання пізнавати нове.
Тема: Теорема Піфагора
Мета:
навчальна: сформулювати і довести теорему Піфагора, розширити пізнання про життя великого математика і про знамениту теорему, навчити учнів застосовувати теорему під час розв’язування задач на практиці і в повсякденному житті;
розвивальна: розвивати логічне мислення, пізнавальний інтерес, навички аргументованої мови, акуратність при побудові малюнків;
виховна: виховувати в учнів відповідальне ставлення до навчання; бажання пізнавати нове.
Тип уроку: засвоєння знань і вмінь.
Обладнання: конспект уроку, роздатковий матеріал, підручник, ПК (телефон) з інтернетом, «Сlassroom», «Google Meet» .
Хід уроку
|
Учні класу |
Дитина з ООП |
||||||||||||||||||
|
І. ІІ.
ІІІІІ.
IV.
V.
VІ.
VІІ.
VІІІ
|
Організаційний етап уроку Перевірка домашнього завдання Перевірка завдання заданого за підручником Виконання завдань на встановлення відповідності Установити відповідність між сторонами
(1 – 3) та їх назвами (А – Г)
1В, 2Г, 3Б.
Актуалізація опорних знань Проводимо графічний диктант із самоперевіркою: 1. Трикутник з кутом 90 ̊ називається прямокутним. Так 2. Сторона, що лежить навпроти прямого кута – катет. Ні 3. Якщо трикутник прямокутний та рівнобедрений, то його гострі кути по 60̊ Ні 4. Сума гострих кутів прямокутного трикутника дорівнює 90 ̊ . Так 5. В прямокутному трикутнику навпроти кута в 30 ̊ лежить катет, що дорівнює половині гіпотенузи. Так 6. Сторони, що утворюють прямий кут називають катетами. Так
Вивчення нового матеріалу Епіграфом нашого уроку є слова Піфагора Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя. Ім’я якого відомого математика складається з трьох складів? Причому перший склад - число, другий – нота, а третій – одне з імен давньоєгипетського бога Сонця (Піфагор) На сьогоднішньому уроці ознайомимося з доведеннями теореми Піфагора; застосовуватимемо її при розв’язуванні задач. Історичні факти, теорема та її доведення на ст 5- 6
Застосування нових знань і вмінь Установіть послідовність слів у теоремі Піфагора: дорівнює, сумі, квадрат, катетів, гіпотенузи, квадратів.
Робота з підручником ст 117 Розв’язати № 529, 530(1), 532 Додаткові завдання
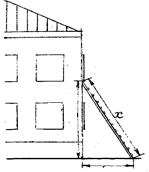
Так, гіпотенуза 15 м, 3*15=45м. Залишок 2 м
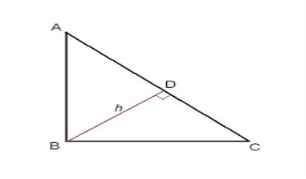
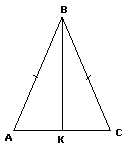
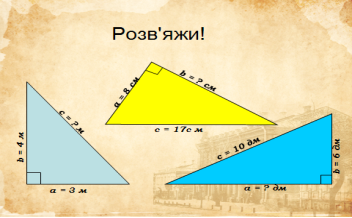
Знайти: ВК. Розв’язання. Оскільки трикутник рівнобедрений, то медіана ВК є і висотою, тому Δ АВК – прямокутний, < К = 900. АВ = 50 м, АК = 14 м (бо К – середина сторони АС). За теоремою Піфагора визначимо невідомий катет. ВК2 = АВ2 – АК2. т.т. ВК2 = 502 – 142 = (50 – 14) x x (50 + 14) = 36 x 64, тоді ВК = 6 x 8 = 48 м. Відповідь: 48 м. Самостійна робота Учні діляться на групи: Хлопці світло синій трикутник, дівчата темно синій. Жовтий трикутник, хто швидше, при умові розв’язавши задачу із трикутником свого кольору. Схематичні малюнки в зошит із усіма позначеннями
Підбиття підсумків уроку Вправа «Закінчіть речення»: 1. Квадрат гіпотенузи дорівнює… ; 2. Квадрат катета дорівнює… ; 3. Єгипетський трикутник це трикутник з вимірами… Домашнє завдання Опрацювати параграф. 16, Розв’язати №531 (1, 3), №533 Творче завдання: з’ясувати чому теорему Піфагора називають “Теорема нареченої», «ослячим містком»? Як відомо, малюнок до теореми Піфагора для випадку рівнобедреного трикутника, учні називали “піфагоровими штанами”, які на всі боки рівні. У Франції і Німеччині теорему Піфагора називали “ослячим містком” (якщо учень не зумів через нього “перейти”, то це був справжній осел). Ще відомо, що в деяких списках «Начал» Евкліда ця теорема називалася «теоремою німфи» за схожість креслення з метеликом, що грецькою називалося німфою. Але словом цим греки називали ще деяких богинь, а також взагалі молодих жінок і наречених. При перекладі з грецької арабський перекладач, не звернувши уваги на креслення, переклав слово «німфа» як «наречена», а не «метелик». Так з’явилася ще одна назва знаменитої теореми — «теорема нареченої». |
Асистент вчителя перевіряє готовність учня до уроку, та наявність домашнього завдання
За допомогою асистента вчителя виконує завдання
Частково розуміє і називає сторони та їх назви
Слухає питання вчителя, асистент вчителя дублює при необхідності
За допомогою асистента вчителя виконує завдання
Малює схематично трикутник, позначає сторони, що відомо за допомогою асистента.
Переписує завдання із дошки
Працює в парі з учителем
Самостійно вибирає будь який трикутник та знаходить невідому сторону.
Опрацювати конспект Розв’язати № 531(1)
|
|||||||||||||||||
Піфагор, чиїм іменем названа теорема, - давньогрецький математик, який жив у VI ст. до н.е. Зі своїми учнями він досліджував властивості чисел, геометричних фігур, небесних світил. Теорема, яку тепер називають теоремою Піфагора була відома ще за 1000 років до Піфагора вченим Вавилону, Єгипту, Китаю. Піфагору належить заслуга доведення цієї теореми і застосування її при розв’язуванні задач.
Біографічна довідка про Піфагора Самоського.
В VI столітті до н.е. у сім’ї золотих справ майстра Мнесарха народився син. Історичні дослідження датують його появу на світ приблизно 580 роком до нашої ери на острові Самос. Можливості дати сину гарну освіту та виховання у Мнесарха були. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримує знання основ музики та живопису. Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жреців. Спочатку він живе на острові Лесбос у свого родича Зоїла. Там відбувається знайомство Піфагора з філософом Ферекідом - другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим на той час наукам. Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи. Але Фалес радить йому поїхати до Єгипту, щоб продовжити навчання.
І Піфагор відправляється у дорогу. Перед Єгиптом Піфагор на деякий час зупиняється у Фінікії, де, за легендою, навчається у відомих сідонських жреців. А потім йому вдається потрапити в єгипетські храми, куди чужоземців не пускали. Щоб прилучитися до таємниць єгипетських храмів, Піфагор приймає посвячення в сан жреця. Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу.
До цього періоду відноситься подія, яка змінила все його майбутнє життя. Помер фараон Амазіс, а його наступник по трону не сплатив щорічну данину Камбізу, персидському царю, що служило достатнім приводом для війни. Перси не помилували навіть священні храми. Піддалися гонінням і жреці: їх вбивали або брали в полон. Так потрапив у персидський полон і Піфагор.
Дванадцять років знаходився у вавилонському полоні Піфагор, доки його не звільнив персидський цар Дарій Гістасп, який прочув про відомого грека. Піфагору вже 60, він вирішує повернутися батьківщину. Піфагор створив власну філософську школу. Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Учні цієї школи зобов’язувались вести так званий піфагорійській спосіб життя.
...Пройшло 20 років після створення школи. Слава про неї рознеслася по всьому світу. Одного разу до Піфагора прийшов Кілон, людина багата, але зла, бажаючи в нетверезому стані вступити до школи. Піфагор відмовив і тоді Кілон розпочав боротьбу з Піфагором. Підпалив його будинок. Під час пожежі піфагорійці врятували життя своєму вчителю, після чого Піфагор засумував і невдовзі помер.
Теорема Піфагора.
-
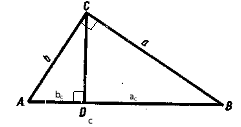 У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів: c2=a2+b2
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів: c2=a2+b2
Дано:трикутник АВС, кут С=90°
Довести: АВ2=АС2+ВС2
Запропонувати доведення теореми декількома способами.
На сьогодні існує близько 150 доведень цієї теореми.
І мабуть Піфагор був не першим, хто довів її. Проте завдяки йому ця теорема перейшла з практичної галузі у наукову.
Сума квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі
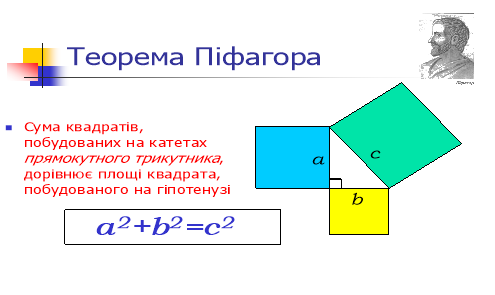
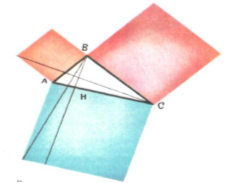 Стародавні геометри не володіли алгебраїчним апаратом, тому теорему Піфагора формулювали так: площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на його катетах.
Стародавні геометри не володіли алгебраїчним апаратом, тому теорему Піфагора формулювали так: площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі площ квадратів, побудованих на його катетах.
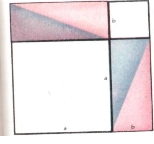
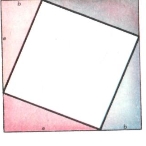 Таке доведення дійшло до нас з персидських рукописів, де замість доведення написано ДИВИСЬ!
Таке доведення дійшло до нас з персидських рукописів, де замість доведення написано ДИВИСЬ!


про публікацію авторської розробки
Додати розробку