Конспект уроку з геометрії у 9 класі на тему " Розв"язування вправ "(Теорема косинусів)

Тема   Розв’язування вправ

Мета:    формувати вміння і навички розв’язування трикутника за трьома його основними елементами;   повторити теорему  косинусів та наслідки з неї;   основні типи задач на обчислення елементів довільних трикутників ,  активізувати роботу учнів відпрацьовувати вміння робити логічні висновки; розвивати пошукову пізнавальну активність, логічне мислення, уяву, зв’язне мовлення; виховувати самостійність, працелюбність, наполегливість, прагнення до самоосвітньої діяльності, впевненість у собі, інтерес до предмету.

Тип уроку: формування умінь та навичок

Обладнання : підручник, конспект, роздатковий матеріал

Хід уроку

І. Організаційний етап.

ІІ. Перевірка домашнього завдання.

Бліц-опитування

1. Які види трикутників за кутами ви знаєте?
2. Які види трикутників за сторонами ви знаєте?
3. Як називається третя сторона в рівнобедреному трикутнику?
4. Що називається синусом кута (косинусом)?
5. Що таке нерівність трикутника?
6. Як називається трикутник зі сторонами 3,4,5?
7. Що означає розв’язати трикутник?
8. Сформулюйте теорему косинусів.

ІІІ. Оголошення теми та мети уроку. Мотивація навчальної діяльності.

Математика застосовується абсолютно скрізь. Зараз математика застосовується не тільки в астрономії, механіці, фізиці, хімії і техніці, де вона застосовувалася і раніше, але також – у біології, суспільних науках і навіть у мовознавстві. Математики передбачають погоду, обчислюють орбіти штучних супутників, курси кораблів, перекладають наукові тексти з однієї мови на іншу.

Знання стають міцнішими, якщо вони застосовуються у практичній діяльності.

Епіграфом до нашого уроку буде висловлювання Блеза Паскаля:

 «Серед рівних розумом – за однакових інших умов – переважає той, хто знає геометрію».

             Пропоную

Не  просто слухати, а чути;

Не  просто дивитися, а бачити;

Не   просто відповідати, а

міркувати;

дружно   і плідно працювати.

Трикутник… знайомий вам з дитинства, і починаючи з 7 класу, з уроків геометрії, геометрична фігура, містить в собі чимало цікавого та загадкового, як Бермудський трикутник, в якому безслідно зникають кораблі та літаки. Знайомі вам фігури квадрат, паралелограм, прямокутник, ромб, трапеція складаються з 2 трикутників, якщо провести одну діагональ, та з 4 трикутників, якщо провести 2 діагоналі.

На попередніх уроках ви розглянули  теореми синусів, косинусів та наслідки з них, ввели поняття розв’язування трикутників, розглянули основні типи задач на обчислення елементів довільних трикутників.

Сьогодні  перед нами стоїть задача:

• повторити все, що вивчили;
• пригадати те, що забули;
• вміло застосовувати отримані знання до розв’язування геометричних задач.

Незважаючи на те, що попереду у нас велика робота, я сподіваюсь, що ми зможемо зберегти гарний настрій до кінця уроку, а якщо вдасться, то ще його й покращимо.

Але перш, ніж ми почнемо я прошу звернути вашу увагу на «Пам’ятку для учнів». Ознайомтесь, будь-ласка, із запропонованими вам рекомендаціями. Якщо ви будете слідувати їм, то я впевнена, що сьогодні на уроці все буде якнайкраще                                         

                                                     Справжній скарб для людини – вміння трудитися.

                                                                                                                      Езоп

                                             Пам’ятка для учнів.

1. Будь уважним.
2. Міркуй, шукай, порівнюй, роби висновки, працюй.
3. Шукай нові способи розв’язування проблеми.
4. Самостійно встановлюй зв’язки відомого з невідомим.
5. Будь наполегливим і не бійся помилитися.
6. Експериментуй та виправляй невдалі спроби.
7. Будь упевнений у своїх здібностях.

Для початку зробимо не великий екскурс в історію.

Історична довідка.

Теорема Піфагора – перше твердження, яке пов’язувало довжини сторін прямокутного трикутника. Згодом люди дізналися, як вимірювати довжини сторін і величини кутів гострокутного і тупокутного трикутників. Виникла наука «тригонометрія» («тригон» – по грецьки означає «трикутник»). Ця наука широко використовується в життєвих ситуаціях, а саме: для вимірювання висоти предмета, вимірювання відстані до недоступної точки.

Повідомлення учнів

1. Причини зародження тригонометрії.

Наприкінці ХV ст. італійський мандрівник Христофор Колумб відкрив узбережжя Америки. Слідом за ним туди зробив кілька подорожей інший італієць – Америго Віспуччі. Португалець Васко да Гама відкрив морський шлях на Індію. Незабаром кораблі Магеллана вперше в історії зробили навколосвітню подорож. Почалася епоха великих географічних відкриттів, завоювань нових територій, освоєння незліченних багатств нових земель.

Не тільки окремі групи купців і мореплавців, але і цілі держави боролися за право експлуатації нових земель. Потрібні були більш потужні і швидкохідні судна, точні географічні карти, досконалі способи орієнтування в відкритому океані.

Створити все це неможливо було без точного математичного розрахунку. Для виконання цих розрахунків елементарної геометрії Евкліда часто не вистачало. Необхідні були нові способи, нові методи в математиці, і, зокрема, в геометрії.

Все це і багато чого іншого привело до необхідності розвивати астрономію – науку про рух небесних тіл, а розвиток астрономії був неможливий без розвитку тригонометрії.

2    Теорема косинусів відома ще стародавнім грекам. У твердженнях 12 і 13 другої книги “Начал” Евкліда розглянуто питання про квадрат сторони трикутника, яка лежить проти гострого і   проти тупого кута. Формулювання обох теорем схожі, тому, здавалося б, лишалося небагато: звести обидва твердження в одне. Але зробити цього греки не змогли, бо не мали розвиненої тригонометрії. Безпосередньо для плоских трикутників теорему косинусів довів арабський астроном і математик Абу-л-Вафа (940-988). Дещо пізніше доводить і використовує цю теорему знаменитий середньоазіатський вчений-енциклопедист ал-Біруні (973-1048).  В Європі теорему косинусів по-справжньому оцінив і почав систематично використовувати знаменитій французький алгебраїст Франсуа Вієт (1540-1603). Вважають, що теорему косинусів вперше довів вчитель ал- Біруні іракський математик ібн-Ірак (помер бл.1020 р.). Доведення цієї теореми зустрічається і в працях ал-Біруні.

 Теорема косинусів була доведена, звичайно, геометрично ще в «Началах» Евкліда.

     Словесно теорема косинусів була вперше сформульована французьким  математиком Француа Вієтом в ХVI столітті.

Сучасний вид теорема косинусів приймає в 1801 році у французького математика Лазара Карно.

ІV Актуалізація опорних знань.

1. Теоретичний бліц-турнір.

Перелік запитань

1.   В чому полягає «розв’язування трикутників»?
2.   Скільки елементів трикутника мають бути відомими, щоб його можна було розв’язувати?
3.   Сформулюйте теорему косинусів.
4.   Сформулюйте наслідок про співвідношення між кутами трикутника і протилежними сторонами.
5.   Сформулюйте теорему про суму кутів трикутника.

2. Метод «Спіймай помилку».

Неправильно:

1) ;

2)

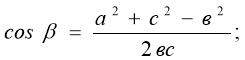
3 )

V. Формування вмінь та навичок.

Робота  з підручником

 Розв’язування задач фронтально, з коментуванням

№2.6   № 2.9

Робота в парах

Задача 1 Дві сторони трикутника дорівнюють 6 см. і 9 см., а косинус кута між ними, дорівнює    Знайдіть третю сторону трикутника.

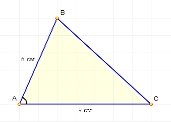                                                       Дано:  

  см.;

  см.;

 Знайти: ВС - ?

Розв’язання:

см.

Відповідь: см.

Задача за готовим малюнком;

Задача 2.

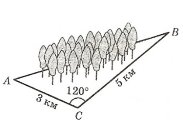Розв’язання:

км.

VІ. Підсумок уроку.

1 «Так чи ні?»

1. Теорема косинусів справедлива для будь-якого трикутника.
2. За теоремою косинусів можна знайти невідому сторону трикутника, якщо відомі його сторона і два кути.
3. За трьома сторонами можна розв’язати трикутник.
4. с²=а²+в²-2авcos.
5. У трикутнику проти більшого кута лежить менша сторона.

2. Закінчити речення:

1. Сьогодні на уроці я повторив …

2. Сьогодні на уроці я навчився …

 3. Необхідно додатково попрацювати над …

4. Найважчим для мене було…

^{VІІ. Домашнє завдання.}