Контрольні роботи з геометрії. 9 клас
У збірнику подано тексти контрольних робіт до всіх тем шкільного курсу геометрії 9 класу, згідно з «Навчальною програмою для загальноосвітніх навчальних закладів. Математика 5-9 класи», затвердженою наказом Міністерства освіти та науки України від 07.06.2017 № 804.Тексти контрольних робіт складені у форматі зовнішнього незалежного оцінювання, що надасть учням можливість у процесі виконання цих робіт психологічно адаптуватися і в подальшому успішно скласти державну підсумкову атестацію, пройти зовнішнє незалежне оцінювання. Також використання даного збірника допоможе вчителеві у здійсненні ефективного контролю засвоєння учнями навчального матеріалу.
Кожна контрольна робота представлена у чотирьох варіантах, які містять завдання початкового, середнього, достатнього та високого рівнів. На її виконання відводиться 45 хвилин.
Анотація
У збірнику подано тексти контрольних робіт до всіх тем шкільного курсу геометрії 9 класу, згідно з «Навчальною програмою для загальноосвітніх навчальних закладів. Математика 5-9 класи», затвердженою наказом Міністерства освіти та науки України від 07.06.2017 № 804. Тексти контрольних робіт складені у форматі зовнішнього незалежного оцінювання, що надасть учням можливість у процесі виконання цих робіт психологічно адаптуватися і в подальшому успішно скласти державну підсумкову атестацію, пройти зовнішнє незалежне оцінювання. Також використання даного збірника допоможе вчителеві у здійсненні ефективного контролю засвоєння учнями навчального матеріалу.
Кожна контрольна робота представлена у чотирьох варіантах, які містять завдання початкового, середнього, достатнього та високого рівнів. На її виконання відводиться 45 хвилин.
Завдання 1-4 — це завдання тестової форми із однією правильною відповіддю; 5-е — на встановлення відповідності (за винятком контрольної роботи № 4 з алгебри, де завдання такого типу відсутнє). Ці завдання відповідають початковому та середньому рівню знань. Завдання вважається виконаним правильно, якщо учень записав правильний варіант відповіді. Завдання 6-9 відповідають достатньому та високому рівню знань, потребують обґрунтування кожного етапу розв’язання та запису відповіді, тобто, є завданнями відкритої форми з розгорнутою відповіддю.
Максимальна кількість балів, яку може отримати учень правильно розв’язавши всі завдання контрольної роботи, — 12 балів.
Зміст
|
Анотація |
1 |
|
Розділ 1. Контрольні роботи з геометрії |
3 |
|
Контрольна робота №1. Метод координат на площині |
3 |
|
Контрольна робота №2. Вектори на площині |
7 |
|
Контрольна робота №3. Розв’язування трикутників |
11 |
|
Контрольна робота №4. Правильні многокутники. Довжина кола. Площа круга |
15 |
|
Контрольна робота №5. Геометричні переміщення |
19 |
|
Контрольна робота №6. Підсумкова |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольні роботи з геометрії 9 клас
Контрольна робота №1.
Метод координат на площині
Варіант 1.
- (1 бал) Чому дорівнює sin1150:
|
А |
Б |
В |
Г |
Д |
|
sin650 |
cos650 |
-sin650 |
-cos650 |
cos1150 |
-
(1 бал) Яка з точок є серединою відрізка АВ, якщо А(-3;8), В(-5;4)
|
А |
Б |
В |
Г |
Д |
|
(4;6) |
(4;-6) |
(-4;6) |
(1;2) |
(-1;-2) |
- (1 бал) Назвіть координати центра кола заданого рівнянням
(х-5)2+(у+1)2=4:
|
А |
Б |
В |
Г |
Д |
|
(5;1) |
(-5;1) |
(-5;-1) |
(2;1) |
(5;-1) |
-
(1 бал) Якій із прямих належить точка М(3;4)?
|
А |
Б |
В |
Г |
Д |
|
у=2х-2 |
5х-3у=7 |
у= -2х-2 |
-2х+7у=3 |
у= -4 |
|
1 |
2х-3у=0 |
А |
паралельна осі ординат |
|
2 |
у-3=0 |
Б |
перпендикулярна прямій у=2х+4 |
|
3 |
5х-4=0 |
В |
проходить через початок координат |
|
4 |
4х+2у=8 |
Г |
паралельна прямій у= -2х+5 |
|
|
|
Д |
паралельна осі абсцис |
- (2 бали) Встановіть відповідність між рівнянням прямої (1-4) та її розташуванням відносно осей координат чи інших прямих (А-Д):
- (3 бали) Вершинами трикутника є точки D(1;5), М(-4;7), N(8;-3). Знайдіть довжину медіани DК трикутника DМN.
- (3 бали) Скласти рівняння кола з центром в точці О(1;-2), яке дотикається до прямої 2х - 4=0.
Контрольна робота №1.
Метод координат на площині
Варіант 2.
-
(1 бал) Чому дорівнює cos1420:
|
А |
Б |
В |
Г |
Д |
|
sin1420 |
cos380 |
sin380 |
–cos380 |
-sin380 |
-
(1 бал) Яка з точок є серединою відрізка АВ, якщо А(8;-3), В(4;-5)
|
А |
Б |
В |
Г |
Д |
|
(4;6) |
(-4;-6) |
(6; -4) |
(12;-8) |
(4;-8) |
- (1 бал) Назвіть координати центра кола заданого рівнянням
(х+3)2+(у-4)2=16:
|
А |
Б |
В |
Г |
Д |
|
(3;4) |
(-3;4) |
(-3;-4) |
(3;-4) |
(0;4) |
-
(1 бал) Якій із прямих належить точка K(2;-5)?
|
А |
Б |
В |
Г |
Д |
|
7х-9=0 |
2х-5у=14 |
у= -5x+5 |
у=5 |
-3x+4у=3 |
5. (2 бали) Встановіть відповідність між рівнянням прямої (1-4) та її розташуванням відносно осей координат чи інших прямих (А-Д):
|
1 |
-6х-2у=0 |
А |
паралельна осі ординат |
|
2 |
7x+3у=0 |
Б |
перпендикулярна прямій у=3х+15 |
|
3 |
|
В |
проходить через початок координат |
|
4 |
у= -8 |
Г |
паралельна прямій у= -3х+15 |
|
|
|
Д |
паралельна осі абсцис |
- (3 бали) Вершинами трикутника є точки X(-3;1),Y(2;-2), Z(-4;6). Знайдіть довжину медіани XA трикутника XYZ.
- (3 бали) Скласти рівняння кола з центром в точці M(-3;2), яке дотикається до прямої 7х+14=0.
Контрольна робота №1.
Метод координат на площині
Варіант 3.
-
(1 бал) Обчисліть сosα, якщо sinα=0,4, α — тупий кут:
|
А |
Б |
В |
Г |
Д |
|
0,4 |
2 |
-2 |
-0.4 |
обчислити неможливо |
- (1 бал) Точка О є серединою відрізка АВ. Які координати точки В, якщо О(1;2), А(3;4).
|
А |
Б |
В |
Г |
Д |
|
(-1;0) |
(2;3) |
(-2;3) |
(0;1) |
(0;0) |
-
(1 бал) Назвіть координати центра кола заданого рівнянням (х+5)2+у2=27:
|
А |
Б |
В |
Г |
Д |
|
(5;1) |
(-5;1) |
(1;0) |
(0;5) |
(-5;0) |
-
(1 бал) Якій із прямих належить точка М(-5;4)?
|
А |
Б |
В |
Г |
Д |
|
7х+9у=16 |
-4х-5у=0 |
-3х-4у+5=0 |
3х+9=0 |
-7у+16=0 |
|
1 |
14х-7у+21=0 |
А |
паралельна осі ординат |
|
2 |
-7у+21=0 |
Б |
перпендикулярна прямій у= - |
|
3 |
14х+21=0 |
В |
проходить через початок координат |
|
4 |
14х+7у+21=0 |
Г |
паралельна прямій у= -2х+5 |
|
|
|
Д |
паралельна осі абсцис |
- (2 бали) Встановіть відповідність між рівнянням прямої (1-4) та її розташуванням відносно осей координат чи інших прямих (А-Д):
- (3 бали) Доведіть, що чотирикутник АВСD з вершинами у точках А(0;6), В(5;7), С(4;2), D(-1;1) є ромбом.
- (3 бали) Скласти рівняння кола, яке дотикається до прямих у=4 та х=2, а його центр лежить на осі ординат.
Контрольна робота №1.
Метод координат на площині
Варіант 4.
-
(1 бал) Обчисліть sinα, якщо сosα=-0,8:
|
А |
Б |
В |
Г |
Д |
|
-0,8 |
0,8 |
-0,6 |
обчислити неможливо |
0,6 |
-
(1 бал) Точка О є серединою відрізка АВ. Які координати точки А, якщо О(5;-4), В(3;-2)
|
А |
Б |
В |
Г |
Д |
|
(7;0) |
(7;-6) |
(-7;2) |
(0;-8) |
(3;4) |
-
(1 бал) Назвіть координати центра кола заданого рівнянням х2+(у-3)2=5:
|
А |
Б |
В |
Г |
Д |
|
(0;-3) |
(0;0) |
(0;3) |
(-3;-3) |
(-3;0) |
-
(1 бал) Якій із прямих належить точка М(2;-3)?
|
А |
Б |
В |
Г |
Д |
|
2х+4у-7=0 |
2х+4у+8=0 |
7х+3у=0 |
9х+37=0 |
2у-4=0 |
|
1 |
10х+3у-3=0 |
А |
паралельна осі ординат |
|
2 |
10х-7=0 |
Б |
перпендикулярна прямій у= - |
|
3 |
3у+35=0 |
В |
проходить через початок координат |
|
4 |
10х-2у-3=0 |
Г |
паралельна прямій у= - 3 |
|
|
|
Д |
паралельна осі абсцис |
- (2 бали) Встановіть відповідність між рівнянням прямої (1-4) та її розташуванням відносно осей координат чи інших прямих (А-Д):
- (3 бали) Доведіть, що чотирикутник АВСD з вершинами у точках А(3;-1), В(2;3), С(-2;2), D(-1;-2) є прямокутником.
- (3 бали) Скласти рівняння кола, яке дотикається до прямих у=4 та х=2, а його центр лежить на осі абсцис.
Контрольна робота №2.
Вектори на площині
Варіант 1.
- (1 бал) Вкажіть неправильне твердження:
А. Вектор — напрямлений відрізок.
Б. Рівні вектори лежать тільки на різних прямих.
В. Нульовий вектор — це вектор, у якого початок та кінець співпадають.
Г. Коленіарні вектори лежать на одній прямій або на паралельних прямих.
Д. Одиничний вектор — вектор, у якого довжина дорівнює 1.
-
(1 бал) Знайдіть координати вектора
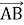 , якщо А(-1;4), В(-3;2):
, якщо А(-1;4), В(-3;2):
|
А |
Б |
В |
Г |
Д |
|
(-3;6) |
(3;8) |
(3; |
(-2;-2) |
(2;2) |
-
(1 бал) У паралелограмі АВСD вкажіть вектори протилежно напрямлені вектору
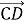 :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Знайдіть скалярний добуток векторів
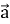 (2;-1) та
(2;-1) та 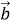 (3;-3):
(3;-3):
|
А |
Б |
В |
Г |
Д |
|
-2 |
1 |
2 |
5 |
9 |
- (2 бали)Установіть відповідність між вектором (1-4) та його координатами (А-Д):
|
1 |
|
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
|
|
4 |
Вектор колінеарний та протилежно напрямлений вектору |
Г |
|
|
|
|
Д |
|
-
(2 бали) При якому значенні р вектори
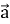 (-5;р) та
(-5;р) та 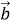 (10;-22) колінеарні?
(10;-22) колінеарні?
-
(2 бали) Діагоналі паралелограма АВСD перетинаються в точці О. Виразіть вектор
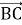 через вектори
через вектори 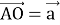 та
та 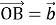 .
.
-
(2 бали) Кут між векторами
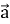 та
та 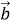 дорівнює 600,
дорівнює 600, 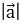 =
=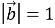 .
.
Обчислити (![]() -
-![]() )(
)(![]() ).
).
Контрольна робота №2.
Вектори на площині
Варіант 2.
- (1 бал) Вкажіть неправильне твердження:
А. Модуль вектора — довжина відрізка, що його зображає.
Б. Скалярний добуток векторів є вектором.
В. Якщо скалярний добуток векторів число від’ємне, то кут між векторами тупий.
Г. Рівні вектори мають однакові координати.
Д. Протилежно напрямлені вектори лежать на одній прямій або на паралельних.
-
(1 бал) Знайдіть координати вектора
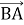 , якщо А(-1;4), В(-3;2):
, якщо А(-1;4), В(-3;2):
|
А |
Б |
В |
Г |
Д |
|
(-3;6) |
(3;8) |
(3; |
(-2;-2) |
(2;2) |
-
(1 бал) У паралелограмі АВСD діагоналі перетинаються в точці О, вкажіть вектори співнапрямлені вектору
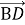 :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Знайдіть скалярний добуток векторів
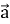 (-3;1) та
(-3;1) та 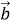 (5;-2):
(5;-2):
|
А |
Б |
В |
Г |
Д |
|
-17 |
-13 |
-1 |
1 |
17 |
- (2 бали) Установіть відповідність між вектором (1-4) та його координатами (А-Д):
|
1 |
|
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
|
|
4 |
Вектор колінеарний та однаково напрямлений вектору |
Г |
|
|
|
|
Д |
|
-
(2 бали) При якому значенні k вектори
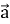 (9;-6) та
(9;-6) та 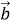 (k;30) колінеарні?
(k;30) колінеарні?
-
(2 бали) Діагоналі паралелограма АВСD перетинаються в точці О. Виразіть вектор
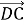 через вектори
через вектори 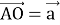 та
та 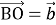 .
.
- (2 бали) Доведіть, що чотирикутник АВСD з вершинами у точках
А(3;-1), В(2;3), С(-2;2), D(-1;-2) є прямокутником.
Контрольна робота №2.
Вектори на площині
Варіант 3.
-
(1 бал) Вкажіть неправильне твердження:
А. Координати нульового вектора (1;1).
Б. Рівні вектори однаково напрямлені та мають однакову довжину.
В. Якщо скалярний добуток векторів додатний, то кут між векторами є гострим.
Г. Одиничний вектор — вектор, у якого довжина дорівнює 1.
Д. Колінеарні вектори мають пропорційні координати. -
(1 бал) Знайдіть координати вектора
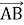 , якщо А(7;-19), В(-5;-15):
, якщо А(7;-19), В(-5;-15):
|
А |
Б |
В |
Г |
Д |
|
(2;-34) |
(-35;285) |
(-12;4) |
(12;-4) |
(-34;2) |
-
(1 бал) У паралелограмі АВСD вкажіть вектори протилежно напрямлені вектору
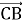 :
:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Знайдіть скалярний добуток векторів
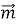 (3;-4) та
(3;-4) та 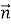 (-4;3):
(-4;3):
|
А |
Б |
В |
Г |
Д |
|
-2 |
8 |
-24 |
0 |
-5 |
- (2 бали) Установіть відповідність між вектором (1-4) та його координатами (А-Д):
|
1 |
Вектор протилежно напрямлений вектору |
А |
|
|
2 |
|
Б |
|
|
3 |
|
В |
|
|
4 |
Вектор колінеарний та однаково напрямлений вектору |
Г |
|
|
|
|
Д |
|
-
(2 бали) При якому значенні k вектори
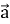 (-4;6) та
(-4;6) та 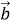 (k;-
(k;- ) коленіарні?
) коленіарні?
-
(2 бали) Діагоналі рівнобічної трапеції АВСD перетинаються в точці О у відношенні 1:2. Виразіть вектор
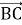 через вектори
через вектори 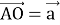 та
та 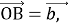 АD — більша основа трапеції.
АD — більша основа трапеції.
-
(2 бали) Кут між векторами
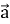 та
та 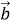 дорівнює 1200,
дорівнює 1200, 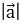 =
=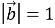 .
.
Обчислити (![]() -3
-3![]() )(
)(![]() ).
).
Контрольна робота №2.
Вектори на площині
Варіант 4.
-
(1 бал) Вкажіть неправильне твердження:
А. Одиничний вектор — вектор, у якого довжина дорівнює 1.
Б. Орт — одиничний вектор, що має напрямок осей координат.
В. Два вектори колінеарні, якщо вони лежать на одній прямій.
Г. Ненульові вектори перпендикулярні, якщо їх скалярний добуток дорівнює нулю.
Д. Рівні вектори мають однакові координати.
-
(1 бал) Знайдіть координати вектора
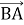 , якщо А(-3;9), В(-4;-7):
, якщо А(-3;9), В(-4;-7):
|
А |
Б |
В |
Г |
Д |
|
(-7;2) |
(7;-2) |
(-16;-1) |
(-1;-16) |
(1;16) |
-
(1 бал) У трапеції АВСD вкажіть вектори співнапрямлені вектору
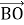 , де О — точка перетину діагоналей:
, де О — точка перетину діагоналей:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Знайдіть скалярний добуток векторів
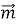 (-4;-2) та
(-4;-2) та 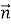 (7;-3):
(7;-3):
|
А |
Б |
В |
Г |
Д |
|
-22 |
34 |
-2 |
- 34 |
2 |
- (2 бали) Установіть відповідність між вектором (1-4) та його координатами (А-Д):
|
1 |
Вектор співнапрямлений вектору 3 |
А |
|
|
2 |
Вектор |
Б |
|
|
3 |
Вектор |
В |
|
|
4 |
Вектор |
Г |
|
|
|
|
Д |
|
-
(2 бали) При якому значенні m вектор
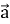 (m;-4) та
(m;-4) та 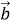 (-8;16) колінеарні.
(-8;16) колінеарні.
-
(2 бали) У рівнобічної трапеції АВСD з меншою основою АВ діагоналі перетинаються в точці О у відношенні 1:3. Виразіть вектор
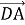 через вектори
через вектори 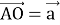 та
та 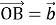 .
.
-
(2 бали) Кут між векторами
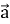 та
та 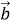 дорівнює 1200,
дорівнює 1200, 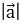 =
=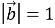 .
.
Обчислити (![]() -3
-3![]() )(
)(![]() ).
).
Контрольна робота №3.
Розв’язування трикутників
Варіант 1.
-
(1 бал) Укажіть правильне твердження:
Квадрат сторони трикутника дорівнює…
А. сумі двох інших сторін.
Б. сумі квадратів двох інших сторін.
В. сумі квадратів двох інших сторін трикутника з подвоєним добутком цих сторін на косинус кута між ними.
Г. сумі квадратів двох інших сторін трикутника без подвоєного добутку цих сторін на косинус кута між ними.
Д. подвоєному добутку інших сторін на косинус кута між ними.
-
(1 бал) Для трикутника KML вкажіть правильне твердження:
А. KM.sin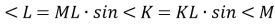
Б.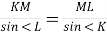 =
=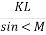 В.
В. 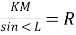
Г.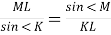 Д.
Д. 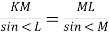
- (1 бал) Площа трикутника KML дорівнює:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1 бал) Чому дорівнює радіус кола описаного навколо рівностороннього трикутника з стороною 6 дм?
|
А |
Б |
В |
Г |
Д |
|
2 |
6 |
12 дм |
6 дм |
3 дм |
- (2 бали) Встановіть відповідність між виразом (1-4) та його значенням (А-Д):
|
1 |
cоs1200 |
А |
|
|
2 |
5-sin2α-cos2α |
Б |
3 |
|
3 |
2+tg450 |
В |
4 |
|
4 |
sin1500 |
Г |
|
|
|
|
Д |
-4 |
-
(3 бали)У трикутнику АВС
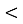 А=
А= В=500, АВ=12см. Знайдіть сторону АС, бісектрису АD, медіану СМ.
В=500, АВ=12см. Знайдіть сторону АС, бісектрису АD, медіану СМ.
- (3 бали) Сторони трикутника дорівнюють 26 см, 28 см, 30 см. Знайдіть найменшу висоту трикутника.
Контрольна робота №3.
Розв’язування трикутників
Варіант 2.
-
(1 бал) Укажіть правильні твердження:
А. сторони трикутника пропорційні до протилежних кутів трикутника.
Б. сторони трикутника пропорційні до косинусів протилежних кутів трикутника.
В. сторони трикутника пропорційні до синусів протилежних кутів трикутника.
Г. сторони трикутника пропорційні одна одній.
Д. сторони трикутника протилежні до синусів кутів трикутника.
- (1 бал) Для трикутника KML вкажіть правильне твердження:
А. KM2=KL2+LM2
Б. KM2=KL2+LM2-2KL.LM Г. KM2=KL2+LM2-2KL.LMсos![]()
В. KM2=KL2+LM2+2KL.LM Д. KM2=KL2+LM2-2KL.LMsin![]()
- (1 бал) Площа трикутника XYZ дорівнює:
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (1 бал) Чому дорівнює радіус кола описаного навколо трикутника з стороною 20 дм та протилежним кутом 300?
|
А |
Б |
В |
Г |
Д |
|
20 дм |
5 |
5 дм |
5 |
2,5 дм |
- (2 бали)Встановіть відповідність між виразом (1-4) та його значенням (А-Д):
|
1 |
sin1500 |
А |
7 |
|
2 |
tg450-4 |
Б |
-3 |
|
3 |
cоs1200 |
В |
-7 |
|
4 |
3+4sin2α+4cos2α |
Г |
|
|
|
|
Д |
|
-
(3 бали)У трикутнику АВС
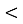 В=400, АВ=ВС=10см. Знайдіть сторону АС, висоту DД, медіану АМ.
В=400, АВ=ВС=10см. Знайдіть сторону АС, висоту DД, медіану АМ.
- (3 бали) Сторони трикутника дорівнюють 14 см, 18 см, 16 см. Знайдіть найбільшу висоту трикутника.
Контрольна робота №3.
Розв’язування трикутників
Варіант 3.
-
(1 бал) Вкажіть неправильне твердження:
А. Найбільша висота проводиться до найменшої сторони.
Б. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших
сторін разом з подвоєним добутком цих сторін на косинус кута між ними.
В. Якщо у трикутнику є тупий кут, то протилежна йому сторона є найбільшою.
Г. Якщо квадрат будь-якої сторони трикутника менший за суму квадратів двох
інших сторін, то протилежний йому кут — гострий.
Д. Сторони трикутника пропорційні синусам протилежних кутів.
-
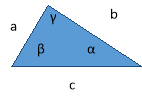
 (1 бал) За малюнком вкажіть правильне твердження:
(1 бал) За малюнком вкажіть правильне твердження:
А.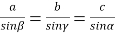 Б.
Б. 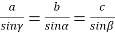
В.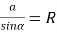 Г.
Г. 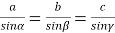 Д. R=asinα
Д. R=asinα
- (1 бал) Площа трикутника АDВ дорівнює:
|
А |
Б |
В |
Г |
Д |
|
АD.DВ.sin |
АD.DВ.соs |
|
|
|
-
(1 бал) Чому дорівнює радіус кола описаного навколо трикутника з стороною 7
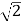 см та протилежним кутом 450?
см та протилежним кутом 450?
|
А |
Б |
В |
Г |
Д |
|
|
14 см |
7 |
10 |
7 см |
- (2 бали)Встановіть відповідність між виразом (1-4) та його значенням (А-Д):
|
1 |
tg 1350 |
А |
1 |
|
2 |
5sin2α+5cos2α-4 |
Б |
|
|
3 |
9-tg450 |
В |
8 |
|
4 |
cоs1200 |
Г |
5 |
|
|
|
Д |
-1 |
- (3 бали) Сторона трикутника дорівнює 26 см, а дві інші утворюють кут 600 і відносяться як 8:3. Знайдіть периметр трикутника.
-
(3 бали) Якщо в трикутнику АВС сторона АВ=4 см, ВС=5 см,
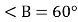 , то чому дорівнює сторона АС, висота АD, медіана АМ?
, то чому дорівнює сторона АС, висота АD, медіана АМ?
Контрольна робота №3.
Розв’язування трикутників
Варіант 4.
- (1 бал) Вкажіть неправильне твердження:
А. Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Б. Проти меншої сторони лежить менший кут.
В. До найбільшої сторони трикутника проводять найменшу висоту.
Г. Сторони трикутника пропорційні синусам протилежних кутів
Д. Радіус описаного кола дорівнює добутку сторони на синус протилежного кута.
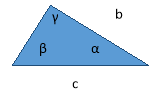
-
(1 бал) За малюнком вкажіть правильне твердження:
А. а2=b2+c2 Б. а2=b2+c2-2bc.cosγ В.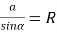
 Г.
Г. ![]() Д.
Д. ![]()
- (1 бал) Площа трикутника OPR дорівнює:
|
А |
Б |
В |
Г |
Д |
|
OP.PR.cos |
|
OP.PR.sin |
OP.PR |
|
-
(1 бал) Чому дорівнює радіус кола описаного навколо трикутника з стороною 8
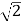 см та протилежним кутом 1350?
см та протилежним кутом 1350?
|
А |
Б |
В |
Г |
Д |
|
16 см |
16 |
8 |
8 см |
|
- (2 бали) Встановіть відповідність між виразом (1-4) та його значенням (А-Д):
|
1 |
cоs1350 |
А |
1 |
|
2 |
13+tg450 |
Б |
|
|
3 |
7-6sin2α-6cos2α |
В |
14 |
|
4 |
sin1200 |
Г |
|
|
|
|
Д |
- |
-
(3 бали) Сторони АВ і АС трикутника АВС утворюють кут 300, а висота проведена з вершини В ділить сторону АС на відрізки АD=12 см і DС=5
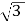 см. Знайдіть сторони трикутника та медіану АМ, проведену до сторони ВС.
см. Знайдіть сторони трикутника та медіану АМ, проведену до сторони ВС.
-
(3 бали) Сторона трикутника дорівнює 2
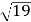 см, а дві інші утворюють кут 600 і відносяться як 5:3. Знайдіть периметр трикутника.
см, а дві інші утворюють кут 600 і відносяться як 5:3. Знайдіть периметр трикутника.
Контрольна робота №4
Правильні многокутники. Довжина кола. Площа круга.
Варіант 1
- (1 бал) Обчисліть радіус кола, вписаного в квадрат зі стороною 8 см.
|
А |
Б |
В |
Г |
Д |
|
4 см |
|
16 см |
|
8 см |
- (1 бал) Визначте кількість сторін правильного многокутника, в якому сума кутів дорівнює 720°.
|
А |
Б |
В |
Г |
Д |
|
4 |
5 |
7 |
6 |
8 |
- (1 бал) Чому дорівнює площа круга, вписаного в квадрат зі стороною 6 см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Чому дорівнює площа круга, довжина якого дорівнює
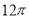 см?
см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між сторонами правильних многокутників (1-4) та радіусами вписаних і описаних кіл (А-Д)
|
1 |
Радіус кола, описаного навколо правильного трикутника зі стороною а |
А |
|
|
2 |
Радіус кола, вписаного в правильний шестикутник зі стороною а |
Б |
|
|
3 |
Радіус кола, описаного навколо правильного чотирикутника зі стороною а |
В |
а |
|
4 |
Радіус кола, вписаного в правильний трикутник зі стороною а |
Г |
|
|
|
|
Д |
|
- (2 бали) Знайдіть площу круга, описаного навколо прямокутника, в якому кут між діагоналями 60°, а менша сторона дорівнює 8 см.
- (2 бали) Знайдіть діаметр кола, якщо його дуга завдовжки 6,28 см має градусну міру 120°.
-
(2 бали) Знайдіть кількість сторін правильного многокутника, якщо довжина кола, вписаного в нього, дорівнює 10π см, а довжина його сторони —
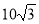 см.
см.
Контрольна робота №4
Правильні многокутники. Довжина кола. Площа круга.
Варіант 2
- (1 бал) Обчисліть радіус кола, описаного навколо квадрата зі стороною 8 см.
|
А |
Б |
В |
Г |
Д |
|
4 см |
|
16 см |
|
14 см |
- (1 бал) Визначте кількість сторін правильного многокутника, в якому сума кутів дорівнює 540°.
|
А |
Б |
В |
Г |
Д |
|
4 |
5 |
7 |
6 |
8 |
- (1 бал) Чому дорівнює площа круга, вписаного в квадрат зі стороною 8см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Чому дорівнює площа круга, довжина якого дорівнює
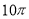 см?
см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між сторонами правильних многокутників (1-4) та радіусами вписаних і описаних кіл (А-Д)
|
1 |
Радіус кола, описаного навколо правильного шестикутника зі стороною а |
А |
|
|
2 |
Радіус кола, вписаного в правильний чотирикутник зі стороною а |
Б |
|
|
3 |
Радіус кола, описаного навколо правильного трикутника зі стороною а |
В |
|
|
4 |
Радіус кола, вписаного в правильний шестикутник зі стороною а |
Г |
|
|
|
|
Д |
а |
- (2 бали) Знайдіть площу круга, описаного навколо прямокутника, в якому кут між діагоналями 60°, а менша сторона дорівнює 10 см.
- (2 бали) Знайдіть діаметр кола, якщо його дуга завдовжки 25,12 см має градусну міру 160°.
-
(2 бали) Знайдіть кількість сторін правильного многокутника, якщо довжина кола, вписаного в нього, дорівнює 6π см, а довжина його сторони —
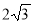 см.
см.
Контрольна робота №4
Правильні многокутники. Довжина кола. Площа круга.
Варіант 3
- (1 бал) Обчисліть радіус кола, описаного навколо правильного трикутника зі стороною 12 см.
|
А |
Б |
В |
Г |
Д |
|
|
6 см |
|
|
|
- (1 бал) Визначте кількість сторін правильного многокутника, в якому сума кутів дорівнює 1080°.
|
А |
Б |
В |
Г |
Д |
|
8 |
9 |
5 |
7 |
6 |
- (1 бал) Чому дорівнює площа круга, вписаного в квадрат зі стороною 10см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Чому дорівнює площа круга, довжина якого дорівнює
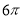 см?
см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між радіусами вписаних і описаних кіл (1-4) та сторонами правильних многокутників (А-Д):
|
1 |
Сторона правильного трикутника, у який вписано коло радіуса r, дорівнює |
А |
|
|
2 |
Сторона правильного чотирикутника, навколо якого описано коло радіуса R, дорівнює |
Б |
|
|
3 |
Сторона правильного трикутника, навколо якого описано коло радіуса R, дорівнює |
В |
R |
|
4 |
Сторона правильного шестикутника, навколо якого описано коло радіуса R, дорівнює |
Г |
|
|
|
|
Д |
|
- (2 бали) Знайдіть площу круга, описаного навколо прямокутника, в якому кут між діагоналями 60°, а менша сторона дорівнює 4 см.
- (2 бали) Знайдіть діаметр кола, якщо його дуга завдовжки 6,28 см має градусну міру 60°.
-
(2 бали) Знайдіть кількість сторін правильного многокутника, якщо довжина кола, вписаного в нього, дорівнює 12π см, а довжина його сторони —
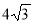 см.
см.
Контрольна робота №4
Правильні многокутники. Довжина кола. Площа круга.
Варіант 4
- (1 бал) Обчисліть радіус кола, вписаного в правильний трикутник зі стороною 12 см.
|
А |
Б |
В |
Г |
Д |
|
|
|
6 см |
|
|
- (1 бал) Визначте кількість сторін правильного многокутника, в якому сума кутів дорівнює 1080°.
|
А |
Б |
В |
Г |
Д |
|
8 |
9 |
7 |
5 |
6 |
- (1 бал) Чому дорівнює площа круга, вписаного в квадрат зі стороною 4см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
-
(1 бал) Чому дорівнює площа круга, довжина якого дорівнює
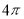 см?
см?
|
А |
Б |
В |
Г |
Д |
|
|
|
|
|
|
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між радіусами вписаних і описаних кіл (1-4) та сторонами правильних многокутників (А-Д):
|
1 |
Сторона правильного чотирикутника, в який вписано коло радіуса r, дорівнює |
А |
R |
|
2 |
Сторона правильного шестикутника, в який вписано коло радіуса r, дорівнює |
Б |
2r |
|
3 |
Сторона правильного трикутника, у який вписано коло радіуса r, дорівнює |
В |
|
|
4 |
Сторона правильного чотирикутника, навколо якого описано коло радіуса R, дорівнює |
Г |
|
|
|
|
Д |
|
- (2 бали) Знайдіть площу круга, описаного навколо прямокутника, в якому кут між діагоналями 60°, а менша сторона дорівнює 12 см.
- (2 бали) Знайдіть діаметр кола, якщо його дуга завдовжки 62,8 см має градусну міру 200°.
-
(2 бали) Знайдіть кількість сторін правильного многокутника, якщо довжина кола, вписаного в нього, дорівнює 24π см, а довжина його сторони -
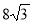 см.
см.
Контрольна робота №5
Геометричні переміщення.
Варіант 1
- (1 бал) Під час переміщення чотирикутника АВСD отримали квадрат А1В1С1D1. Визначте довжину діагоналі АС, якщо В1D1 = 8 см.
|
А |
Б |
В |
Г |
Д |
|
12 см |
6 см |
4 см |
8 см |
16 см |
- (1 бал) Паралельне перенесення задано формулами х1 = х – 4, у1 = у + 5. Знайдіть координати точки, в яку переходить центр кола
(х+2)2 + (у-1)2 = 4.
|
А |
Б |
В |
Г |
Д |
|
(7; -6) |
(-1; 4) |
(-6; 6) |
(2; - 4) |
(-1; 6) |
- (1 бал) Сторона одного рівностороннього трикутника вдвічі більша, ніж сторона другого рівностороннього трикутника. Знайдіть площу більшого трикутника, якщо площа меншого трикутника дорівнює 8 см2.
|
А |
Б |
В |
Г |
Д |
|
16 см2 |
32 см2 |
64 см2 |
24 см2 |
48 см2 |
-
(1 бал) У результаті гомотетії з центром В трикутник АВС переходить у трикутник А1ВС1. Знайдіть коефіцієнт гомотетії, якщо ВС = 12 см,
В1С1 = 3 см.
|
А |
Б |
В |
Г |
Д |
|
4 |
|
|
2 |
9 |
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між координатами точок (1-4) та їх образами (А-Д):
|
1 |
Точка (-2; 4) у результаті симетрії відносно початку координат переходить в точку |
А |
(6; 2) |
|
2 |
Точка (-2; 4) у результаті симетрії відносно точки (2; 3) переходить в точку |
Б |
(2; -4) |
|
3 |
Точка (-2; 4) у результаті симетрії відносно прямої х = -1 переходить в точку |
В |
(2; 2) |
|
4 |
Точка (-2; 4) у результаті симетрії відносно прямої у = 1 переходить в точку |
Г |
(0; 4) |
|
|
|
Д |
(-2; -2) |
- (3 бали) Кінці діаметра кола розташовані в точках А і В. Складіть формули паралельного перенесення, внаслідок якого дане коло переходить у коло (х + 2)2 + (у – 3)2 = 16, якщо А(3; 2), В(3; 10).
- (3 бали) Знайдіть площу трапеції з висотою 12 см, подібної до рівнобічної трапеції, в якій основи дорівнюють 30 см і 50 см, а бічні сторони — 26 см.
Контрольна робота №5
Геометричні переміщення.
Варіант 2
- (1 бал) Під час переміщення чотирикутника АВСD отримали квадрат А1В1С1D1. Визначте довжину діагоналі АС, якщо В1D1 = 12 см.
|
А |
Б |
В |
Г |
Д |
|
12 см |
6 см |
4 см |
8 см |
16 см |
- (1 бал) Паралельне перенесення задано формулами х1 = х – 4, у1 = у + 5. Знайдіть координати точки, в яку переходить центр кола (х-3)2 + (у+1)2 = 9.
|
А |
Б |
В |
Г |
Д |
|
(7; -6) |
(-1; 4) |
(-6; 6) |
(2; - 4) |
(-1; 6) |
- (1 бал) Сторона одного рівностороннього трикутника вдвічі більша, ніж сторона другого рівностороннього трикутника. Знайдіть площу більшого трикутника, якщо площа меншого трикутника дорівнює 16 см2.
|
А |
Б |
В |
Г |
Д |
|
16 см2 |
32 см2 |
64 см2 |
24 см2 |
48 см2 |
-
(1 бал) У результаті гомотетії з центром В трикутник АВС переходить у трикутник А1ВС1. Знайдіть коефіцієнт гомотетії, якщо ВС = 6 см,
В1С1 = 3 см.
|
А |
Б |
В |
Г |
Д |
|
4 |
|
|
2 |
9 |
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між координатами точок (1-4) та їх образами (А-Д):
|
1 |
Точка (3; -5) у результаті симетрії відносно початку координат переходить в точку |
А |
(-5; -5) |
|
2 |
Точка (3; -5) у результаті симетрії відносно точки (2; 3) переходить в точку |
Б |
(3; -1) |
|
3 |
Точка (3; -5) у результаті симетрії відносно прямої х = -1 переходить в точку |
В |
(-3; 5) |
|
4 |
Точка (3; -5) у результаті симетрії відносно прямої у = -3 переходить в точку |
Г |
(1; 11) |
|
|
|
Д |
(5; 5) |
- (3 бали) Кінці діаметра кола розташовані в точках А і В. Складіть формули паралельного перенесення, внаслідок якого дане коло переходить у коло (х + 2)2 + (у – 3)2 = 16, якщо А(2; 1), В(2; 9).
- (3 бали) Знайдіть площу трапеції з висотою 12 см, подібної до рівнобічної трапеції, в якій основи дорівнюють 14 см і 50 см, а бічні сторони — 30 см.
Контрольна робота №5
Геометричні переміщення.
Варіант 3
- (1 бал) Під час переміщення чотирикутника АВСD отримали квадрат А1В1С1D1. Визначте довжину діагоналі АС, якщо В1D1 = 6 см.
|
А |
Б |
В |
Г |
Д |
|
12 см |
6 см |
4 см |
8 см |
16 см |
- (1 бал) Паралельне перенесення задано формулами х1 = х – 4, у1 = у + 5. Знайдіть координати точки, в яку переходить центр кола (х+1)2 + (у-2)2 = 4.
|
А |
Б |
В |
Г |
Д |
|
(-5; 7) |
(-1; 4) |
(-3; 3) |
(5; - 7) |
(-1; 6) |
- (1 бал) Сторона одного рівностороннього трикутника вдвічі більша, ніж сторона другого рівностороннього трикутника. Знайдіть площу більшого трикутника, якщо площа меншого трикутника дорівнює 6 см2.
|
А |
Б |
В |
Г |
Д |
|
16 см2 |
32 см2 |
64 см2 |
24 см2 |
48 см2 |
-
(1 бал) У результаті гомотетії з центром В трикутник АВС переходить у трикутник А1ВС1. Знайдіть коефіцієнт гомотетії, якщо ВС = 3 см,
В1С1 = 12 см.
|
А |
Б |
В |
Г |
Д |
|
4 |
|
|
2 |
9 |
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між координатами точок (1-4) та їх образами (А-Д):
|
1 |
Точка (-1; 3) у результаті симетрії відносно початку координат переходить в точку |
А |
(5; 3) |
|
2 |
Точка (-1; 3) у результаті симетрії відносно точки (2; 3) переходить в точку |
Б |
(-3; -3) |
|
3 |
Точка (-1; 3) у результаті симетрії відносно прямої х = 1 переходить в точку |
В |
(1; -3) |
|
4 |
Точка (-1; 3) у результаті симетрії відносно прямої у = -1 переходить в точку |
Г |
(3; 3) |
|
|
|
Д |
(-1; -5) |
- (3 бали) Кінці діаметра кола розташовані в точках А і В. Складіть формули паралельного перенесення, в наслідок якого дане коло переходить у коло (х + 2)2 + (у – 3)2 = 16, якщо А(5; 3), В(5; 11).
- (3 бали) Знайдіть площу трапеції з висотою 10 см, подібної до рівнобічної трапеції, в якій основи дорівнюють 20 см і 50 см, а бічні сторони — 25 см.
Контрольна робота №5
Геометричні переміщення.
Варіант 4
- (1 бал) Під час переміщення чотирикутника АВСD отримали квадрат А1В1С1D1. Визначте довжину діагоналі АС, якщо В1D1 = 4 см.
|
А |
Б |
В |
Г |
Д |
|
12 см |
6 см |
4 см |
8 см |
16 см |
- (1 бал) Паралельне перенесення задано формулами х1 = х – 4, у1 = у + 5. Знайдіть координати точки, в яку переходить центр кола (х-3)2 + (у+2)2 = 4.
|
А |
Б |
В |
Г |
Д |
|
(-5; 7) |
(-1; 3) |
(-3; 3) |
(5; - 7) |
(-7; 7) |
- (1 бал) Сторона одного рівностороннього трикутника вдвічі більша, ніж сторона другого рівностороннього трикутника. Знайдіть площу більшого трикутника, якщо площа меншого трикутника дорівнює 4 см2.
|
А |
Б |
В |
Г |
Д |
|
16 см2 |
32 см2 |
64 см2 |
24 см2 |
48 см2 |
-
(1 бал) У результаті гомотетії з центром В трикутник АВС переходить у трикутник А1ВС1. Знайдіть коефіцієнт гомотетії, якщо ВС = 6 см,
В1С1 = 12 см.
|
А |
Б |
В |
Г |
Д |
|
4 |
|
|
2 |
9 |
- (За кожну правильну відповідь – 0,5 бала) Установіть відповідність між координатами точок (1-4) та їх образами (А-Д)
|
1 |
Точка (3; -2) у результаті симетрії відносно початку координат переходить в точку |
А |
(5; 3) |
|
2 |
Точка (3; -2) у результаті симетрії відносно точки (2; 3) переходить в точку |
Б |
(-3; 2) |
|
3 |
Точка (3; -2) у результаті симетрії відносно прямої х = 1 переходить в точку |
В |
(3; 6) |
|
4 |
Точка (3; -2) у результаті симетрії відносно прямої у = 2 переходить в точку |
Г |
(1; 8) |
|
|
|
Д |
(-1; -2) |
- (3 бали) Кінці діаметра кола розташовані в точках А і В. Складіть формули паралельного перенесення, внаслідок якого дане коло переходить у коло (х + 2)2 + (у – 3)2 = 16, якщо А(4; -1), В(4; 7).
- (3 бали) Знайдіть площу трапеції з висотою 6 см, подібної до рівнобічної трапеції, в якій основи дорівнюють 20 см і 30 см, а бічні сторони — 13 см.
Контрольна робота №6
Підсумкова.
Варіант 1
-
(1 бал) У трикутнику АВС
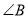 =60°,
=60°, 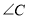 = 45°. Знайдіть довжину сторони АВ, якщо АС=
= 45°. Знайдіть довжину сторони АВ, якщо АС= 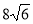 см.
см.
|
А |
Б |
В |
Г |
Д |
|
|
16 см |
10 см |
|
8 см |
-
(1 бал) Обчисліть модуль вектора
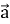 , якщо
, якщо 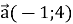 .
.
|
А |
Б |
В |
Г |
Д |
|
5 |
3 |
|
|
6 |
- (1 бал) Точка С — середина відрізка АВ. Знайдіть координати точки А, якщо В(-2; 3), С(1; 4).
|
А |
Б |
В |
Г |
Д |
|
(3; 1) |
(1; 14) |
(-1; 9) |
(4; 5) |
(-4; 5) |
-
(1 бал) У трикутнику АВС
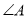 = 60°, АВ = 5 см, АС = 7 см. Знайдіть довжину сторони ВС.
= 60°, АВ = 5 см, АС = 7 см. Знайдіть довжину сторони ВС.
|
А |
Б |
В |
Г |
Д |
|
2 см |
|
|
|
8 см |
- (За кожну правильну відповідь — 0,5 бала) Установіть відповідність між фігурами (1-4) та їх площами (А-Д):
|
1 |
Площа ромба з діагоналями 10 см і 36 см дорівнює |
А |
48 см2 |
|
2 |
Площа круга, вписаного в квадрат зі стороною 20 см, дорівнює |
Б |
180 см2 |
|
3 |
Площа трикутника зі сторонами 13 см, 14 см, 15 см дорівнює |
В |
314 см2 |
|
4 |
Площа паралелограма з діагоналями 12 см, 8см та кутом між ними 30° дорівнює |
Г |
24 см2 |
|
|
|
Д |
84 см2 |
- (2 бали) Знайдіть основу рівнобедреного трикутника, в якому бічна сторона і медіана, проведена до неї, відповідно дорівнюють 8 см і 6 см.
- (2 бали) Знайдіть координати вершини А паралелограма АВСD, якщо
В(3; 1), С(6; -2), D(-3; -2).
-
(2 бали) В трапеції основи дорівнюють 1 см і 3 см, а бічні сторони 4 см і
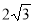 см. Знайдіть кут, який утворює більша бічна сторона з більшою основою трапеції.
см. Знайдіть кут, який утворює більша бічна сторона з більшою основою трапеції.
Контрольна робота №6
Підсумкова.
Варіант 2
-
(1 бал) У трикутнику АВС
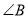 =60°,
=60°, 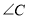 = 45°. Знайдіть довжину сторони АВ, якщо АС=
= 45°. Знайдіть довжину сторони АВ, якщо АС= 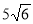 см.
см.
|
А |
Б |
В |
Г |
Д |
|
|
16 см |
10 см |
|
8 см |
-
(1 бал) Обчисліть модуль вектора
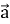 , якщо
, якщо 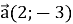 .
.
|
А |
Б |
В |
Г |
Д |
|
5 |
3 |
|
|
6 |
- (1 бал) Точка С — середина відрізка АВ. Знайдіть координати точки А, якщо В(3; -4), С(2; 5).
|
А |
Б |
В |
Г |
Д |
|
(3; 1) |
(1; 14) |
(-1; 9) |
(4; 5) |
(-4; 5) |
-
(1 бал) У трикутнику АВС
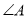 = 30°, АВ =
= 30°, АВ = 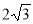 см, АС = 4 см. Знайдіть довжину сторони ВС.
см, АС = 4 см. Знайдіть довжину сторони ВС.
|
А |
Б |
В |
Г |
Д |
|
2 см |
|
|
|
8 см |
- (За кожну правильну відповідь — 0,5 бала) Установіть відповідність між фігурами (1-4) та їх площами (А-Д):
|
1 |
Площа ромба з діагоналями 8 см і 24 см дорівнює |
А |
360 см2 |
|
2 |
Площа круга, вписаного в квадрат зі стороною 10 см, дорівнює |
Б |
240 см2 |
|
3 |
Площа трикутника зі сторонами 36 см, 29 см, 25см дорівнює |
В |
96 см2 |
|
4 |
Площа паралелограма з діагоналями 24 см, 20см та кутом між ними 30° дорівнює |
Г |
78,5 см2 |
|
|
|
Д |
120 см2 |
- (2 бали) Знайдіть основу рівнобедреного трикутника, в якому бічна сторона і медіана, проведена до неї, відповідно дорівнюють 6 см і 4 см.
-
(2 бали) Знайдіть координати вершини А паралелограма АВСD, якщо
В(4; 2), С(2; -3), D(-4; -3). -
(2 бали) В трапеції основи дорівнюють 1 см і 3 см, а бічні сторони 4 см і
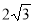 см. Знайдіть кут, який утворює менша бічна сторона з більшою основою трапеції.
см. Знайдіть кут, який утворює менша бічна сторона з більшою основою трапеції.
Контрольна робота №6
Підсумкова.
Варіант 3
-
(1 бал) У трикутнику АВС
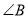 =60°,
=60°, 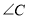 = 45°. Знайдіть довжину сторони АВ, якщо АС=
= 45°. Знайдіть довжину сторони АВ, якщо АС= 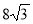 см.
см.
|
А |
Б |
В |
Г |
Д |
|
|
16 см |
10 см |
|
|
-
(1 бал) Обчисліть модуль вектора
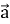 , якщо
, якщо 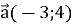 .
.
|
А |
Б |
В |
Г |
Д |
|
5 |
3 |
|
|
6 |
- (1 бал) Точка С — середина відрізка АВ. Знайдіть координати точки А, якщо В(-4; 5), С(3; 1).
|
А |
Б |
В |
Г |
Д |
|
(3; 1) |
(-3; 10) |
(-1; 9) |
(10; -3) |
(4; -5) |
-
(1 бал) У трикутнику АВС
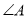 = 30°, АВ = 5 см, АС =
= 30°, АВ = 5 см, АС = 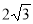 см. Знайдіть довжину сторони ВС.
см. Знайдіть довжину сторони ВС.
|
А |
Б |
В |
Г |
Д |
|
2 см |
|
|
|
16 см |
- (За кожну правильну відповідь — 0,5 бала) Установіть відповідність між фігурами (1-4) та їх площами (А-Д):
|
1 |
Площа ромба з діагоналями 8 см і 13 см дорівнює |
А |
60 см2 |
|
2 |
Площа круга, вписаного в квадрат зі стороною 30 см, дорівнює |
Б |
18 см2 |
|
3 |
Площа трикутника зі сторонами 29 см, 25 см, 6см дорівнює |
В |
706,5 см2 |
|
4 |
Площа паралелограма з діагоналями 10 см, 18см та кутом між ними 30° дорівнює |
Г |
52 см2 |
|
|
|
Д |
45 см2 |
- (2 бали) Знайдіть основу рівнобедреного трикутника, в якому бічна сторона і медіана, проведена до неї, відповідно дорівнюють 16 см і 12 см.
- (2 бали) Знайдіть координати вершини А паралелограма АВСD, якщо
В(2; -5), С(1; -2), D(-2; 1).
-
(2 бали) В трапеції основи дорівнюють 2 см і 6 см, а бічні сторони 8 см і
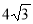 см. Знайдіть кут, який утворює більша бічна сторона з більшою основою трапеції.
см. Знайдіть кут, який утворює більша бічна сторона з більшою основою трапеції.
Контрольна робота №6
Підсумкова.
Варіант 4
-
(1 бал) У трикутнику АВС
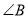 =60°,
=60°, 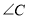 = 45°. Знайдіть довжину сторони АВ, якщо АС=
= 45°. Знайдіть довжину сторони АВ, якщо АС= 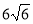 см.
см.
|
А |
Б |
В |
Г |
Д |
|
|
12 см |
8 см |
|
|
-
(1 бал) Обчисліть модуль вектора
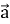 , якщо
, якщо 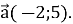
|
А |
Б |
В |
Г |
Д |
|
5 |
9 |
|
|
6 |
- (1 бал) Точка С — середина відрізка АВ. Знайдіть координати точки А, якщо В(-2; 5), С(2; -3).
|
А |
Б |
В |
Г |
Д |
|
(-3; 1) |
(3; -10) |
(1; 9) |
(6; -11) |
(4; -5) |
-
(1 бал) У трикутнику АВС
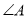 = 30°, АВ = 2 см, АС =
= 30°, АВ = 2 см, АС = 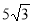 см. Знайдіть довжину сторони ВС.
см. Знайдіть довжину сторони ВС.
|
А |
Б |
В |
Г |
Д |
|
49 см |
|
|
|
7 см |
- (За кожну правильну відповідь — 0,5 бала) Установіть відповідність між фігурами (1-4) та їх площами (А-Д):
|
1 |
Площа ромба з діагоналями 8 см і 13 см дорівнює |
А |
1256 см2 |
|
2 |
Площа круга, вписаного в квадрат зі стороною 40 см, дорівнює |
Б |
15 см2 |
|
3 |
Площа трикутника зі сторонами 5 см, 5 см, 6 см дорівнює |
В |
90 см2 |
|
4 |
Площа паралелограма з діагоналями 5 см, 12 см та кутом між ними 30° дорівнює |
Г |
12 см2 |
|
|
|
Д |
|
- (2 бали) Знайдіть основу рівнобедреного трикутника, в якому бічна сторона і медіана, проведена до неї, відповідно дорівнюють 12 см і 8 см.
- (2 бали) Знайдіть координати вершини А паралелограма АВСD, якщо
В(-1; 1), С(2; 3), D(1; -1).
-
(2 бали) В трапеції основи дорівнюють 2 см і 6 см, а бічні сторони 8 см і
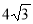 см. Знайдіть кут, який утворює менша бічна сторона з більшою основою трапеції.
см. Знайдіть кут, який утворює менша бічна сторона з більшою основою трапеції.
1


про публікацію авторської розробки
Додати розробку
