Конспект уроку з математики для 6 класу на тему: " Коло. Довжина кола".

Тема уроку. Коло. Довжина  кола.

Мета уроку. Формувати компетентності учнів:     

математичну: освітню: формування знань про геометричні фігури (коло) на площині, їх властивості, а також умінь застосовувати вивчене у процесі розв’язування геометричних задач;

розвивальну: розвиток логічного, критичного і творчого мислення учнів, здатності чітко та аргументовано формулювати і висловлювати свої судження; забезпечення інтелектуального розвитку учнів, розвитку їх уваги, пам’яті, логіки, культури мислення та інтуїції;

дослідницьку: формуванням здатності учня перевіряти справедливість гіпотези,

 процедурну: формування здатності учня використовувати на практиці алгоритми розв’язування типових задач;

 самоосвіти і саморозвитку:  спонукати учнів до написання  повідомлень ;

інформаційну: стимулювання учнів до використання додаткової інформації,   вміння самостійно шукати, аналізувати та відбирати необхідну інформацію;

комунікативну: стимулювання вміння учнів висловлювати власну точку зору; вміння працювати в групі;

соціальну: надання учням можливості виявлення ініціативи.

Спосіб реалізації:  через діяльнісний підхід - розвиток умінь і навичок

кожного учня,  формування здібностей до колективної діяльності та самоосвіти.

Тип уроку. Вивчення нового матеріалу.

Наочність і обладнання.  Комп’ютер, нитки, лінійка, олівець, циркуль.

    І. Організаційний момент

Взаємне  вітання вчителя й учнів; перевірка відсутніх; перевірка зовнішнього стану приміщення; перевірка робочих місць; організація уваги.

                                               Слайд 2.

 Сьогодні ви відкриєте одне з визначних чисел, яке не можна записати числом.

ІІ. Перевірка домашнього завдання. Актуалізація опорних знань

Зараз я пропоную вам виконати дані вправи і розшифрувати слово. Працюємо парами.

                                                     Слайд 3.

Отже, це слово «коло»

ІІІ. Повідомлення теми  уроку і очікуваних результатів

Слайд 1.

На уроці ви  повинні  оволодіти наступними знаннями: пояснювати, що таке  коло, записувати і пояснювати формулу довжини кола, зображати та знаходити на малюнках  коло, розв’язувати  вправи, що передбачають  знаходження довжини кола

ІV. Мотивація навчальної діяльності.

 Термін «Коло» досить часто звучить в нашому житті: під час дитячих ігор вас частенько запрошували стати в коло, у вас є особисте коло друзів. В Польщі є місто Коло, народний танець «Коло». Навколо нас як в архітектурі так і в природі  достатньо часто зустрічаємо  «коло», навіть не рахуючи коліс автомобілів, велосипедів і т.д. До речі, подивіться на вигляд перших коліс,  інформація про які дійшла до нас. Сьогодні ми будемо вести розмову  про коло як математичне поняття.

          Хто з вас може намалювати коло? Що ви ще знаєте про нього? Чи знаєте ви як обчислити довжину кола? Послухайте ці рядки вірша. А чи справді це відношення довжини кола до діаметра завжди є незмінним? Чому ж воно дорівнює?

                                                       Слайд 4.

Вам потрібно перевірити математичний факт, викладений у вірші. Отже, на нас чекає дослідницька практична робота. Приготуйте необхідні креслярські інструменти, ми починаємо дослідження.

V. Сприймання  і  усвідомлення нового матеріалу

    Що таке коло і довжина кола?...

Уявлення про коло дають кермо автомобіля, каблучка тощо.

1. Формування поняття кола

Практична робота з побудови кола радіусом 3 см.

Алгоритм.

Позначимо на площині деяку точку О.

Поставимо ніжку циркуля з голкою в точку О.

Виміряємо розхил циркуля 3 см.

Іншою ніжкою циркуля описуємо коло.

Усі точки кола розміщені на відстані 3 сантиметри від центра.

                                                  Слайд 5.                                               Слайд 6.

 2. Формування знань про радіус кола

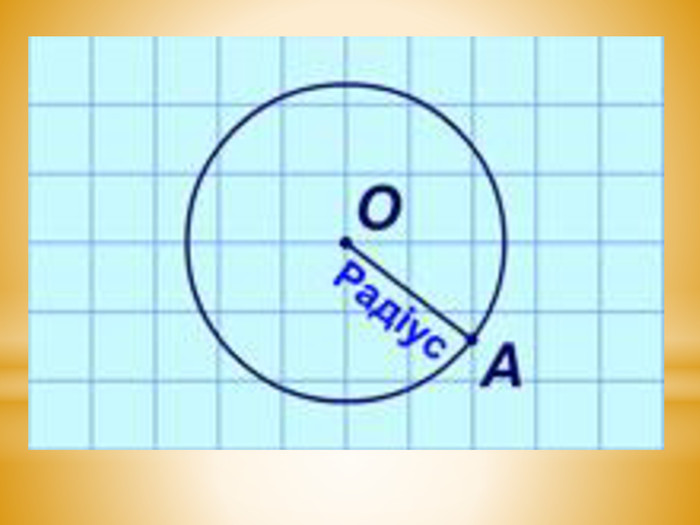
1.Побудова радіуса кола.

2. Означення радіуса кола.

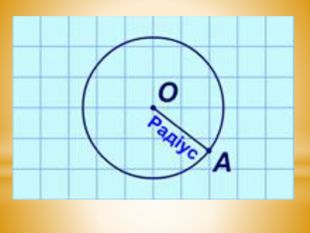
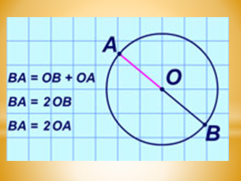
Сполучимо відрізком центр кола з довільною точкою цього кола (А).

Відрізок ОА (а також його довжину) називають радіусом кола.

Радіус побудованого кола дорівнює 3 см.

Радіусом кола називають відрізок, що сполучає будь-яку точку кола з центром.

                                                     Слайд 7.

3. Формування знань про  діаметр  кола

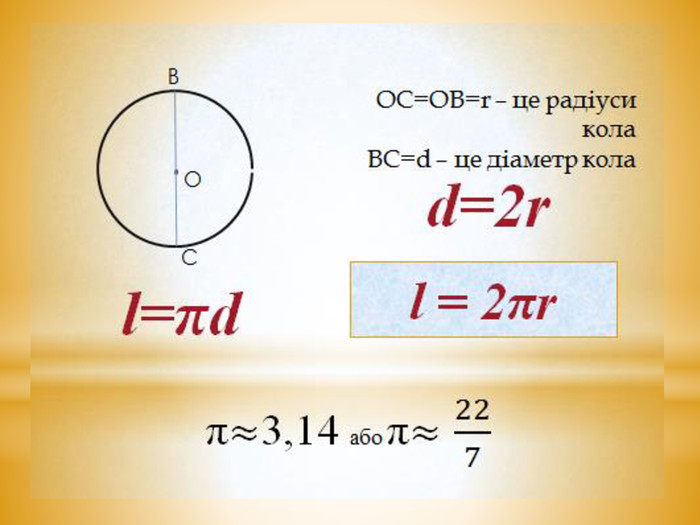
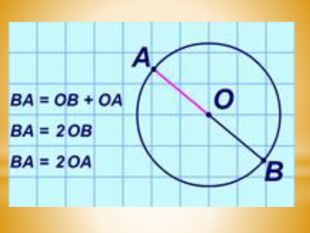
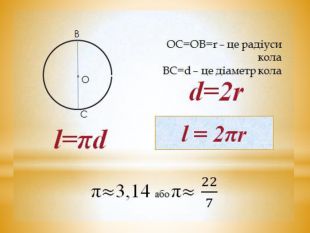
Відрізок, що сполучає дві точки кола і проходить через його центр (а також довжину цього відрізка), називають діаметром.

 
4. Встановлення залежності  між  радіусом та діаметром.

Діаметр кола удвічі довший від радіуса цього кола.

                                                     Слайд 8                                                    Слайд 9.

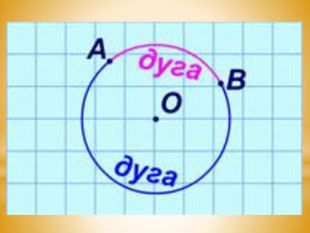
5.Формування знань про   дугу кола.

Дві точки А та В, що лежать на колі, розбивають його на дві частини. Кожну із цих частин називають дугою кола.

Точки А та В — кінці цих дуг. Якщо точки А та В є кінцями діаметра, то вони розбивають коло на дві рівні частини, кожну з яких називають півколом.

                                                               Слайд 10.

 6. Формування вмінь застосовувати знання на практиці

Дослідницька робота.

Як обчислити довжину кола?

Тема роботи: Довжина кола.

Обладнання: Циркуль. Лінійка. Нитка.

Хід роботи

І група бере радіус 3 см,

ІІ група бере радіус 3,5 см.

ІІІ група обирає круглий предмет.

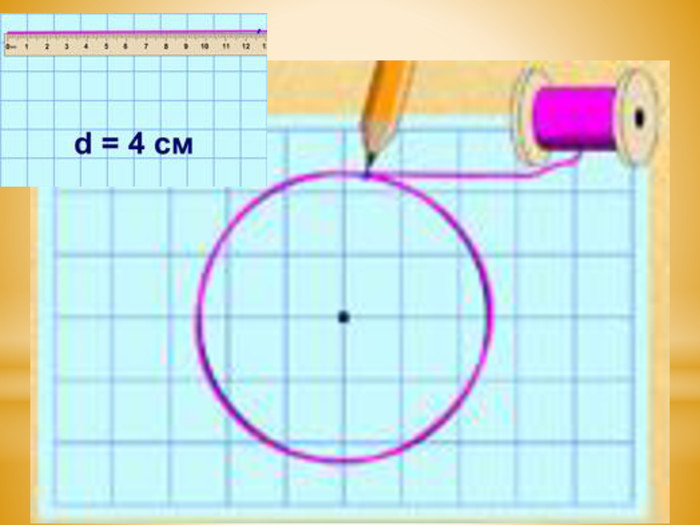
1. Будуємо коло, радіус якого становить 2 см.

2. Накладаємо на коло нитку.

3. Ставимо ручкою відмітку на нитці в тій точці, в якій нитка збігається зі своїм початком.

                                                        Слайд 11.

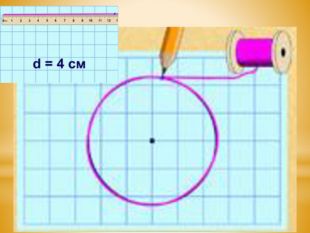
4. Розгортаємо нитку та вимірюємо її довжину до відмітки. Ця довжина дорівнює довжині кола.

5. Діаметр кола d становить 4 см. Довжина кола С дорівнює 12,6 см.

6. Знаходимо відношення .

Порівнюються результати всіх груп. Робиться висновок.

Виявляється, що для всіх кіл відношення довжини кола до довжини його діаметра є одним і тим же числом. Це число позначають грецькою літерою π. Його записують нескінченним десятковим дробом

π = 3,1415926.... 

C: d= π , звідки C= π d.

Довжина кола дорівнює добутку числа π на діаметр кола.

Як можна записати довжину кола через радіус?...(Вислуховуються пропозиції учнів)

Правильно! Оскільки діаметр кола дорівнює двом радіусам, то довжина кола радіуса r дорівнює 2 π r. Маємо ще одну формулу для довжини кола:

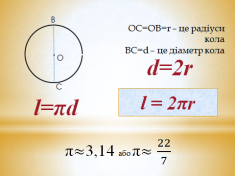С =2πr   π 3,14 

                                                   Слайд 12.

 7. Первинне усвідомлення вивченого.

Накресли коло, радіус якого дорівнює 2 см. 

Де лежать точки, розміщена від центра на відстані 1 см; 2 см; 3 см?

Точка А, відстань від якої до центра дорівнює 2 см, належить колу.

Точка В, відстань від якої до центра дорівнює 1 см, лежить усередині кола.

Точка С, відстань від якої до центра дорівнює 3 см, лежить зовні кола.

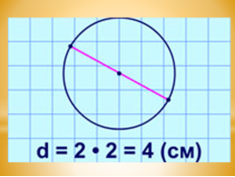
Чому дорівнює діаметр кола?

Діаметр кола    d=  2∙2 = 4 (см).

VІ.  Фізкультхвилинка.
Учні отримують половину карточки і, прочитавши свою карточку, повинні об’єднатися в пари, щоб одержати правильне твердження.

VІІ. Первинне застосування нового матеріалу

1.               Знайдіть діаметр кола, якщо радіус дорівнює 3,5 м? (7см)
2.               Накресліть коло і проведіть в ньому два взаємно перпендикулярні діаметри.
3.               Знайдіть радіус кола, якщо діаметр дорівнює  5 м? (2,5м)
4.               Знайдіть довжину кола, радіус якого 2,5 м. (≈15,7м)
5.               Знайдіть діаметр кола, довжина якого дорівнює 62,8см. (≈20 см)
6.               Знайдіть радіус кола, довжина якого дорівнює 0,628 км.( ≈100м)

Задача 1. Який шлях проходить за 2 години кінець хвилинної стрілки, довжина якої дорівнює 1,5см? ( ≈18,84см)

Задача 2. Творче завдання.

 Знайдіть довжину паса, натягнутого на два шківи, якщо радіус кожного з них дорівнює 0,4м, а відстань між їх центрами – 2,5м.

Розв’язання.

Довжина паса складається з довжин двох відрізків по 2,5м, відстань між центрами кіл, та довжини двох півкіл, що разом утворюють коло, радіусом  0,4м. l ≈2*3,14*0,4+ 2*2,5=7,512 (м).

Відповідь. ≈7,512м.

VІІІ. Домашнє завдання

Слайд Творче завдання.

1. Довжину кола збільшили з 6,28см до 12,56 см. На скільки збільшився радіус кола?

 2. «Колесо винайшли українці?»  результат подати  у вигляді презентації чи повідомлення.

 Слайд 16.

ІХ. Підсумок   уроку. Оцінювання. Рефлексія

Про що нове ви  дізналися на уроці?

Що ви же засвоїли?

Що вам треба ще довчити?

А чи запам’ятали ви число «пі»?

На завершення уроку познайомтеся з його Величністю Пі

Слайди 13,14 ,15

5. Про значення  числа Пі  є такий вірш у підручнику  математики   Л.П.Магницького.

22 совы скучали

На больших сухих суках.

22 совы мечтали

О 7 больших мышах,

О мышах довольно юрких,

 В  аккуратных серых шкурках.

Слюнки капали с усов.

У огромных серых сов. (Це двадцять дві сьомих)

6.А хто такий Магницький? Підготуйте невеличке повідомлення.