Конспект уроку з математики для 6 класу на тему: " Круг. Площа круга. ".
- урок _круг.pptx pptx
- урок_круг.docx docx
Тема уроку. Круг. Площа круга.
Мета уроку. Формувати в учнів компетентності:
математичні: освітні: забезпечення оволодіння учнями мовою геометрії, умінь виконувати геометричні побудови (кола і круга);формування знань про геометричні фігури (коло і круг) на площині, їх властивості, а також умінь застосовувати вивчене у процесі розв’язування геометричних задач; формування знань про основні геометричні величини (довжина, площа), способи їх знаходження ;
дослідницьку: формування здатності учня перевіряти справедливість гіпотез, спираючись на відомі методи (індукція, аналогія, узагальнення), а також на власний досвід досліджень;
логічну: формування здатності учнів використовувати логічний апарат математичних теорій для розв’язування задач;
навчально-пізнавальну: володіння прийомами дій у нестандартних ситуаціях, володіння вимірювальними навичками;
інформаційну: залучення додаткової інформації в процесі викладання математики, стимулювання учнів до використання додаткової інформації;
полікультурну: використання інформації з історії математичних відкриттів, розв'язування задач історико-культурного змісту;
комунікативну і соціальну:стимулювання вміння учнів висловлювати власну точку зору, удосконалення вмінь дітей формулювати цілі власної діяльності та робити висновки за її результатами, застосування взаємоопитування, залучення до роботи в групах з різнорівневими завданнями; виховання наполегливості, старанності, відповідальності.
Спосіб реалізації: через діяльнісний підхід - розвиток умінь і навичок
кожного учня, формування здібностей до колективної діяльності та самоосвіти.
Тип уроку. Урок засвоєння нових знань
Наочність і обладнання. Циркулі , плакати «Коло . Довжина кола» , «Круг . Площа круга». Комп’ютер. «Презентація»
І. Організаційний момент.
Взаємне вітання вчителя й учнів; перевірка відсутніх; перевірка зовнішнього стану приміщення, організація уваги.
« Математика цікава тоді, коли живить нашу винахідливість і здатність міркувати» . Д. Пойа Отже, цікавої математики вам сьогодні!
І. Перевірка домашнього завдання
- І рівень – звірити відповіді. ІІ рівень - коментарі.
- Творче завдання.

Слайд1.
ІІІ. Актуалізація і корекція опорних знань.
1.«Запитання від однокласника». «Слухай уважно, відповідай швидко»
( Учні з місця називають учня, якому хочуть задати запитання. Якщо товариш не відповідає, то він відповідає сам. Потім передає право задати запитання іншому.) Можливі запитання:
- На рисунку назвати центр кола, радіус кола, діаметр кола.
- Як позначається діаметр, радіус, довжина кола?
- Як пов’язані між собою радіус і діаметр кола?
- За якою формулою обчислюється довжина кола?
- Радіус кола дорівнює 3 см, чому дорівнює діаметр?
- Діаметр кола дорівнює 10см, чому дорівнює радіус?
- Чому дорівнює число Пі?
- Дати означення діаметра кола.
- Дати означення радіуса кола.
- Дати означення дуги кола.
- Дати означення кола.
 2.Дуже добре, а чи не можете ви мені відповісти на запитання: чи однакові фігури зображені на рисунку.( демонстрація слайду)
2.Дуже добре, а чи не можете ви мені відповісти на запитання: чи однакові фігури зображені на рисунку.( демонстрація слайду)
Слайд 2.
ІV. Повідомлення теми, цілей і завдань уроку.
Звичайно, дані фігури різні. Ви правильно міркували, на одному рисунку коло, а на іншому круг. Саме круг – тема нашого уроку. Ви дізнаєтесь, що спільного він має з колом, а чим відрізняється, самі «виведете» формулу для обчислення його площі.

Слайд 3.
V. Мотивування учіння.
Ми вивчаємо коло і круг. Попрошу вас назвати з навколишніх предметів ті, які б мали своїм елементом ці фігури.
( Сонце, горщик для квітів, ручка, олівець, іграшки, колеса велосипедів, машин, салфетки, антени, частини архітектурних споруд тощо) . Отже, нас оточують предмети, які таким чи іншим чином пов’язані з математичними поняттями коло і круг. Вони є частинами механізмів, а отже, щоб ці механізми працювали, потрібно знати властивості цих фігур.



 Слайд 4.
Слайд 4.
Мабуть, частіше всього навколо нас нам нагадує коло і круг колесо.
Самим загадковим є винахід колеса. Здавалось, такий простий механізм..., але людина не зразу до нього прийшла.
Слайди 5,6,7
На уроці ми розглянемо круг як математичне поняття.
 Задачу про визначення відношення довжини кола до його діаметра історично важко відокремити від задачі про «квадратуру круга», тобто побудови квадрата за площею рівного даному кругу, а простіше – знаходження площі круга.
Задачу про визначення відношення довжини кола до його діаметра історично важко відокремити від задачі про «квадратуру круга», тобто побудови квадрата за площею рівного даному кругу, а простіше – знаходження площі круга.
Слайд 8.
В кінці уроку ви зумієте обчислити цю поверхню і дізнаєтесь, як це робили єгиптяни.
VІ. Сприймання й усвідомлення учнями фактичного матеріалу,
|
Крок 1. |
Сформувати поняття круга. |
|
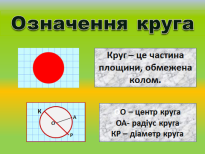
Кожне коло розбиває площину, на якій воно накреслене, на дві частини — внутрішню і зовнішню. Точки кола й усі внутрішні точки утворюють круг. Круг – це частина площини, обмежена колом.
|
|


![]()
|
Крок 2 |
Сформувати знання про елементи круга. |
|
Центр, радіус і діаметр кола називають відповідно центром, радіусом і діаметром цього круга. O – центр круга. OA – радіус круга. KP – діаметр круга. |
|
|
Крок 3 |
Сформувати поняття півкруга, сектора. |
|
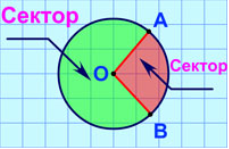
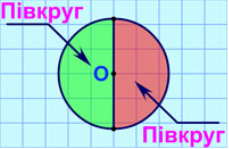
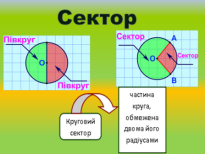
Два радіуси ОА і ОВ розбивають круг на дві частини, кожну з яких називають сектором. Будь-який діаметр розбиває круг на дві рівні частини, які називають півкругами.
|
|
|
Крок 4 |
Сформувати вміння застосовувати знання на практиці. |
|
Практична робота. Обчислення площі круга ( Учні працюють за вказаним алгоритмом) |
|
Мета: 1) Наближено обчислити площу круга.
2) Обчислити відношення площі круга до квадрата радіуса.
3) порівняти отримані результати . Зробити висновок.
4) записати формулу для площі круга.

|
Хід роботи. І група - 4см, ІІ група-3 см, ІІІ- група – 2 см. |
|
1. На аркуші паперу в клітинку будуємо коло, радіус якого дорівнює 4 см 2. Обводимо зовнішній контур тих клітинок, які майже повністю належать кругу. 3. Рахуємо кількість клітинок усередині контуру. 4. Рахуємо кількість клітинок зовні контуру, які частково належать кругу, одержане число ділимо на 2 (тому що в середньому частини двох неповних клітинок дають одну цілу). 5. Додаємо до числа клітинок, які повністю належать кругу, число, одержане в п. 4. 6. Оскільки площа 4 клітинок дорівнює 1 см2, то щоб виразити площу круга у квадратних сантиметрах, ділимо число, отримане в п. 5, на 4. Одержуємо наближене значення площі: S .... 7. Обчислюємо квадрат радіуса круга: r2 = 16 см2.
8. Знаходимо відношення Це число наближене, називається π
У старших класах доведемо, що
|
VІІ. Фізкультхвилинка.
Швидко встали, посміхнулись
Вище-вище потягнулись
Нумо, плечі розпрямили,
Руки вгору, три, чотири.
Вправо, вліво повернулись,
До колін своїх торкнулись.
Сіли, встали. Сіли, встали.
Всі на місце посідали.
Молодці. Сідайте.
VІІІ. Осмислення зв'язків і залежностей між елементами вивченого матеріалу.
Ми сьогодні вивчили фігуру на площині – круг. Перш ніж почати застосовувати теорію на практиці, давайте повторимо її.
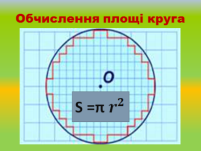
Слайди 9,10,11
Задача 1. Обчисліть площу круга, діаметр якого дорівнює 0,6см.
Розв’язання. S=![]() r2, r=
r2, r=![]() d, r=
d, r= ![]() *0,6=0,3(см).
*0,6=0,3(см).
S![]() 3,14*0,32=3,14*0,09=0,2826 (см2).
3,14*0,32=3,14*0,09=0,2826 (см2).
Відповідь. ![]() 0,3см2.
0,3см2.
Задача 2. Довжина кола 8π см. Знайдіть площу круга, обмеженого цим колом.
Розв’язання. Довжина кола l=2![]() r, 2
r, 2![]() r = 8
r = 8![]() ,r= 4 см. Площа круга S=
,r= 4 см. Площа круга S=![]() r2
r2![]()
![]() 3,14 *42= 3,14*16= 50,24 (см2)
3,14 *42= 3,14*16= 50,24 (см2) ![]() 50см2.
50см2.
Задача 3. Площа круга дорівнює 16πсм2. Знайдіть довжину кола цього ж радіуса.
Розв’язання. S=![]() r2,
r2, ![]() r2=16
r2=16![]() , r2=16, r=4 см. Тоді l = 2
, r2=16, r=4 см. Тоді l = 2![]() r
r![]() 2*3,14*4= =25,12см2
2*3,14*4= =25,12см2
Задача 4.Периметр квадрата, зображеного на рисунку, дорівнює 48 см. Знайдіть радіус круга та площу не заштрихованої частини фігури.
 Розв’язання. Сторона квадрата дорівнює 48:4=12(см).
Розв’язання. Сторона квадрата дорівнює 48:4=12(см).
Сторона квадрата рівна двом радіусам круга. Тоді, . r= 12:2 = 6(см)
Площа круга S![]() 3,14*62=113,04. Площа квадрата S1
3,14*62=113,04. Площа квадрата S1 ![]() 122=144 (см2)
122=144 (см2)
Шукана площа S2 =144 –113,04 = 30,96(см2)
ІХ. Узагальнення і систематизація знань
1.Як називають фігури?
2. Властивості якої фігури ми з вами вивчили? А тепер давайте складемо «Дерево знань». Я пропоную вам слайд зі схемою. Ваше завдання його заповнити.

Слайди 12,13
Х. Домашнє завдання.
 2. Творче завдання.
2. Творче завдання.
Слайд 15.
ХІ. Підсумок уроку . Оцінювання. Рефлексія.
А ми нічого не забули? Чи зможемо ми тепер розв’язати історичну задачу?
Давайте перевіримо,наскільки точними були розрахунки без знання формули.

Слайд 14
1.Що нового ви взнали на уроці?
2.Який матеріал уроку вас зацікавив більше?
3.Які задачі вам видались легкими, а які складними?
4.Чи з’явилось у вас бажання самостійно дізнатися більше?
1


про публікацію авторської розробки
Додати розробку






























