Конспект уроку з математики по темі «Пропорції» 6 клас

Конспект уроку з математики

6 клас.

Тема: «Пропорції. Основна властивість пропорції.

Цілі уроку

1. повторити визначення відношення двох чисел, його сенс, правило знаходження відсоткового відношення двох чисел та «перехресне» правило рівності звичайних дробів;
2. сформувати поняття пропорції, її крайніх та середніх членів, запровадити основну властивість пропорції;
3. сприяти формуванню в учнів здібності до читання та запису пропорції, знаходження невідомих членів пропорції;
4. сприяти подальшому розвитку в учнів уміння робити грамотні математичні записи та формулювання, акуратно оформляти роботу.

Хід уроку:

1.               Організаційний момент.
2.               Перевірка домашнього завдання.
3.               Перевірка знань, умінь та навичок учнів.
4.               Вивчення нового матеріалу.
5.               Підбиття підсумків.
6.               Домашнє завдання.

1. Організаційний момент.

Вчитель перевіряє готовність класу до уроку.

2. Перевірка домашнього завдання.

Вчитель з'ясовує, чи є у учнів питання щодо домашнього завдання.

За допомогою проектора на екран виводиться рішення рівняння і учням пропонується сформулювати правило, що лежить в основі цього рішення (перехресне правило рівності двох звичайних дробів):

Рішення:

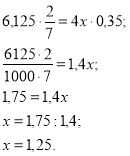
Відповідь

3. Перевірка знань, умінь та навичок учнів.

Усне фронтальне опитування:

•       Що називають ставленням двох чисел?
•       Що свідчить про відношення двох чисел?
•       Продовжи пропозицію: «Ставлення не зміниться, якщо …»
•       Як знайти відсоткове відношення двох чисел?

Математичний диктант (з наступною самоперевіркою):

Варіант 1.        Варіант 2.

1. Чому дорівнює відношення чисел:

20 до 4?       10 до 2?

2. Спростити ставлення:

14 до 21.       18 до 27.

3. Відношення числа

18 до b дорівнює 6.      b до 12 дорівнює 4.

Чому дорівнює число b?

4. Знайдіть відсоткове відношення:

1,2 до 6.        2,5 до 5.

5. Знайдіть відношення величин:

4 см до 1 м.        3 хв. до 1 години.

4.   Вивчення нового матеріалу.

Учні записують у зошитах дату та тему уроку.

Вчитель:  зверніть увагу на №1 із математичного диктанту:

  і .

Отже, - це справжня рівність.

Вчитель: У математиці вже кілька століть для істинної рівності двох відносин існує спеціальна назва – пропорція.

Отже: "Істинна рівність двох відносин називається пропорцією".

Вчитель: Пропорції записують так:

                          або    , де

Вчитель: Читають:  1) «Ставлення a до b дорівнює відношенню c до d».

2) "a відноситься до b як c відноситься до d".

Вчитель: Компоненти пропорції мають свої спеціальні назви (записати у зошиті):

a : b = c : d    або    

Вчитель: Усна вправа: « З'ясуйте, чи ця рівність є пропорцією. Якщо так, то вкажіть крайні члени та середні члени пропорції».

1) 12: 3 = 1: 4; 2)

Вчитель: Звернемо увагу на те, що якщо відносини в пропорції записати за допомогою дробової риси, то пропорцію можна розглядати як правильну рівність двох звичайних дробів і на підставі «перехресного» правила рівності дробів: .

Таким чином, «перехресне» правило є основою розв'язання задач на пропорції і тому його називають основною властивістю пропорції.

Оскільки компоненти пропорції мають свої особливі назви, то основна властивість пропорції читається так:

«Рівність є пропорцією і тоді, коли добуток крайніх членів дорівнює добутку середніх членів».

Вчитель: Записати у зошитах:

Вчитель: Спираючись на основну властивість пропорції, можна сформулювати правила знаходження невідомих членів пропорції:

 1) Щоб знайти крайній член пропорції, треба твір її середніх членів поділити відомий крайній член:

                                         ;     

 2) Щоб знайти середній член пропорції, треба твір її крайніх членів поділити на відомий середній член:

Вчитель: Слід зазначити, що пропорції є математичною моделлю багатьох практичних завдань. Тому кожному корисно знати, що таке пропорція, основна властивість пропорції та вміти знаходити невідомий член пропорції.

Вчитель: Розв'яжемо завдання (вчитель на дошці, учні в зошитах):

Автомобіліст зауважив, що відстань у 21 км він проїхав за 15 хвилин. За скільки часу він подолає 84км, що залишилися, якщо їхати з тією ж швидкістю?

Рішення:

Нехай 84 км машина проїде за х хвилин.

Оскільки швидкість дорівнює відношенню шляху до часу і за умовою вона не змінюється, то (Це пропорція!).

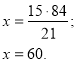
 60 хв = 1ч.

Відповідь: 84 км машина проїде за 1 годину.

5. Підбиття підсумків.

Виставляються оцінки тим, хто працював біля дошки.

Усне фронтальне опитування:

•        Що ми називаємо пропорцією?
•        Сформулюйте основну властивість пропорції.
•        Як знайти невідомий крайній (середній) член пропорції?

6. Домашнє завдання.