Конспект уроку з теми "Показникова функція, її властивості та графік"
К.онспект уроку з теми "Показникова функція, її властивості та графік". Розробка уроку з використанням групової діяльності учнів
РОЗРОБКА УРОКУ ІЗ ВИКОРИСТАННЯМ ТЕХНОЛОГІЇ ГРУПОВОЇ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ ШКОЛЯРІВ
Тема. Показникова функція, її графік та властивості.
Мета. Ввести поняття показникової функції. Розглянути графік показникової функції та її властивості. Формувати вміння будувати графік показникової функції. Вчити використовувати властивості показникової функції при розв’язуванні вправ та робити висновки; розвивати мислення; виховувати культуру мови.
Тип уроку. Урок вивчення нового матеріалу.
Хід уроку
І. Організаційна частина
ІІ. Актуалізація опорних знань учнів
Сьогодні ми почнемо вивчати тему «Показникові функція», тому давайте пригадаємо деякі поняття, які розглядаються при вивчення будь-якої функції.
Питання до учнів.
- Дайте означення функції.
- Які є способи задання функції?
- Що називають областю визначення функції?
- Що називають областю значення функції?
- Яка функція називається зростаючою?
- Яка функція називається спадною?
Завдання. На малюнку зображено графік деякої функції. За допомогою графіка функції знайти: D(y), E(y), проміжки монотонності. (Рис. функції)
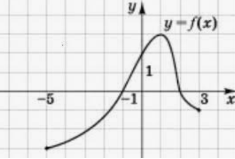
ІІІ. Вивчення нового матеріалу.
Оголошення мети та завдань уроку.
Спочатку розв’яжемо задачі, які підведуть нас до формування означення показникової функції та побудови її графіка.
Задача. Припустимо, що у деякому великому ставку щоденно подвоюється кількість латаття. Якщо спочатку було 5 водяних лілій, скільки їх буде через 1, 2, 3, 4, 5, 10, 60, n днів. Намалювати схему графіка. Про який вид послідовності йдеться?
Розв’язання.
|
Через один день: Через два дні: Через три дні: Через чотири дні: Через п’ять днів: Через десять днів: Через шістдесят днів: Через n днів: |
А1= 5·2 = 5·21 = 10 А2= 5·2·2 = 5·22 = 20 А3= 5·2·2·2 = 5·23 =40 А4= 5·2·2·2·2 = 5·24 = 80 А5= 5·2·2·2·2·2 = 5·25 = 160 А10= 5·210 = 5120 А60= 5·260 Аn= 5·2n |
An – геометрична послідовність.
f(n) = An, де n ![]() N. Намалюємо схему графіка f(n) = An.
N. Намалюємо схему графіка f(n) = An.
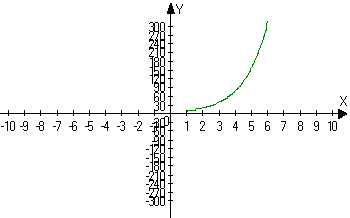
Де буде знаходитись точка, якщо кількість годин буде не натуральне число, а раціональне. (Спочатку з’єднаємо точки плавною лінією; дана точка буде знаходитись на прямій)
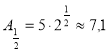
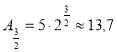
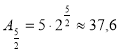
Отже, одержані точки належать графіку функції.

 Учень (показує фотографію білого латаття та розповідає про цю рослину).
Учень (показує фотографію білого латаття та розповідає про цю рослину).
Біле латаття належить до рідкісних та зникаючих рослин. ЛАТАТТЯ (німфея), рід багаторічних водних трав з великим плаваючим листям і різно забарвленими квітками. Існує 50 видів, розповсюджена по всій земній кулі. Латаття біле доходить до 68° північної широти і виживає в промерзаючих водоймищах. Молоді кореневища (у деяких – насіння) їстівні. Декілька видів розводять як декоративні. До роду латаття належить єгипетський (нільський) лотос, з квітками діаметром до 25 см.…
Отже, f(n) = 5·2n можна розглядати як функцію. В загальному вигляді її можна записати f(х) = с·ах, де с – стале число. Функції виду f(х) = с·ах називають експоненціальними, якщо ![]() R+.
R+.
Багато процесів в житті, економіці, суспільстві при певних припущеннях можна наближено описати за допомогою експоненціальних функцій. При цьому часто йдеться про експоненціальне зростання та експоненціальне спадання. Дуже часто в математиці і в багатьох прикладних науках використовується функція ![]() . Її називають експонентою.
. Її називають експонентою.
Якщо с = 1, то отримаємо функцію f(х) = ах.
Вчитель. Чому цю залежність можемо назвати функцією?
Учень. Цю залежність можна назвати функцією тому, що кожному значенню х відповідає єдине значення у.
Означення. Функцію, яку задано формулою у = ах (де а>0, а ≠ 1), називають показниковою функцією.
Вчитель. Які з даних функцій показникові? (на дошці записані функції, учні виписують показникові). Розглядаємо вправу 1.1
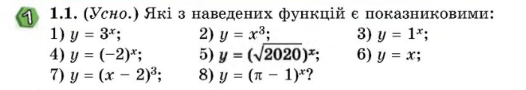
Розглядаємо умови а > 0, а ≠ 1
Вчитель. Чому а > 0 та а ≠ 1
Разом з учнями детально розібрати означення функції.
Якщо а = 1, то отримаємо функцію у = 1х. Це стала функція. Її графік – пряма паралельна осі Ох, яка проходить через точку (0,1).
Якщо а < 0, то вираз ![]() не має змісту.
не має змісту.
Якщо а = 0, то вираз ![]() не мають змісту.
не мають змісту.
Робота в групах
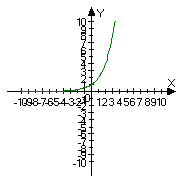
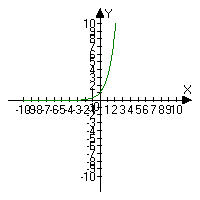
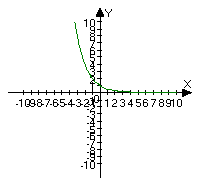
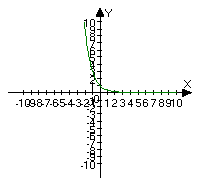
Клас ділиться на чотири групи. Групи будують графіки функцій у=2х, у=3х, 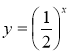 ,
,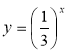 .
.
|
|
|
|
|
|
|
|
|
|
|
|
Вчитель. Охарактеризувати графіки даних функцій. Відповіді учнів. Кожна група характеризує свій графік. Функції ![]() та
та ![]() зростають, а функції
зростають, а функції 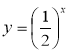 та
та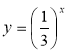 – спадають.
– спадають.
Розміщені в І та ІІ чвертях.
Всі графіки проходять через точку (0;1)
Вчитель. Яка область визначення та область значення цих функцій? D(y) = R, E(y) =(0; +∞).
Вчитель. Навести приклади зростаючих та спадних показникових функцій. (Учні наводять приклади)
Висновок. Отже, якщо а > 1, то функція зростає, а якщо 0 < a < 1 – спадає.
Завдання. Зобразити схематично графіки показникової функції у = ах та записати їх властивості. Виділити спільні властивості.

V. Закріплення вивченого матеріалу
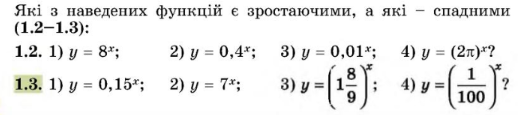
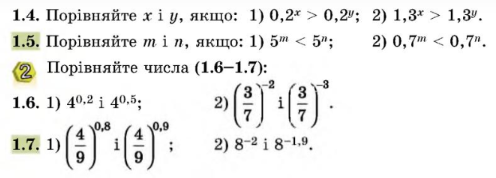
VІ. Підсумок уроку.
- Яку функцію ми сьогодні вивчили?
- Яка функція називається показниковою?
- За якої умови показникові функція зростає? А за якої – спадає?
- Яка область визначення та область значення показникової функції?
- Через яку точку проходить графік кожної показникової функції?
VІІ. Домашнє завдання. Опрацювати §1. Виконати вправи 1.3, 1.5, 1.7. (Підручник: Математика: Алгебра і початки аналізу та геометрія: підр. для 11 кл. (рівень стандарту) Автор: О.С. Істер Видавництво: Київ, "Генеза", 2019)


про публікацію авторської розробки
Додати розробку