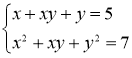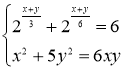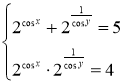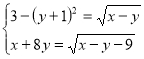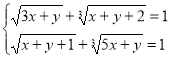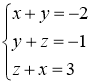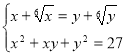Нестандартні методи розв'зування систем

                     Департамент освіти  Харківської міської ради  

 

 

Комунальний заклад «Харківський фізико-математичний ліцей № 27

Харківської міської ради Харківської області»

 

 

 

 

 

 

План – конспект

уроку за темою: «Нестандартні методи    розв’язування систем рівнянь»

 

     у  11 класі

 

 

 

 

 

 

Учитель  математики

вищої кваліфікаційної категорії,

вчитель-методист

Харік Олена Юхимівна

 

 

 

 

 

 

 

 

 

 

 

 

 

15.02.2023

 

 

    Харків

 

 

Тема.  Нестандартні методи розв’язування систем рівнянь

 

Мета. Формування предметних компетентностей:

• актуалізувати та розширити знання про  методи розв’язування систем рівнянь;
• відпрацювати навички розв’язування систем рівнянь;
• розвивати логічне та критичне мислення, пізнавальні інтереси та здібності учнів;
• виховувати прагнення до вдосконалення знань.

  Формування ключових компетентностей:

• уміння вчитися:  формувати вміння аналізувати, робити висновки, мати власну

думку щодо обговорюваних питань;

• комунікативної:  формувати вміння будувати власні висловлювання, доводити

      свою думку;

• соціальної:  формувати навички самостійної роботи, роботи в колективі, набуття досвіду взаємного навчання;
• загальнокультурної:  виявлення особистісного ставлення до себе, результатів

      своєї  роботи; цінувати думку іншого.

 Відпрацьовування прийомів формувального оцінювання.

 

Тип уроку: комбінований

 

Міжпредметні зв’язки: астрономія, фізика, всесвітня історія, зарубіжна література

 

Форми роботи на уроці: фронтальна бесіда, самостійна робота, робота в групах, інтелектуальна гра

 

Інструментарій уроку: мультимедійна презентація вчителя до теми уроку, картки накопичува-льних балів (маршрутний лист, гугл-форма)

 

Очікувані результати:  учні зможуть

• усвідомити об’єктивну необхідність вивчення різноманітних методів розв’язування систем рівнянь;
• виконувати вправи на розв’язування систем рівнянь

 

Девіз уроку:

Знання  - скарбниця, а ключ до неї  -  практика.

                Томас Фуллер

Хід уроку

 

І.   Організаційний момент

     Організація та психологічне налаштування учнів на діловий ритм, спільну працю.

 

ІІ.  Визначення теми і завдань уроку.

      Актуалізація опорних знань та активізація розумової діяльності учнів

 

  1.  Короткий огляд методів розв’язування систем рівнянь:

      

Стандартні		Нестандартні
1	Підстановка (заміна змінних)	1	Область визначення і множина значень
2	Додавання	2	Монотонність функції

 

2. Самостійна робота (1 етап)       https://forms.gle/cYHUGW3QHxVph3nGA                              

                  

Завдання 1.

Завдання 2.

 

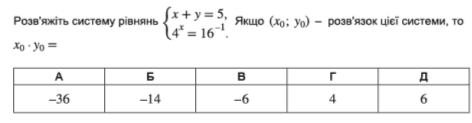
Завдання 3.

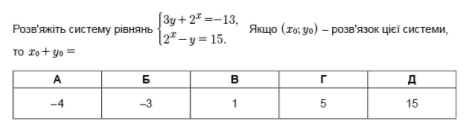
Завдання 4.

   Розв’яжіть систему рівнянь: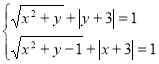

Завдання 5.

   Розв’яжіть систему рівнянь: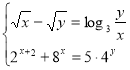

 

2. Самоперевірка робіт, заповнення карток накопичувальних балів (маршрутних листів, гугл-форм).                    

Завдання 1.

;

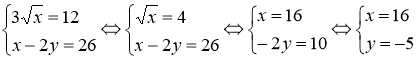Відповідь:  А

Завдання 2.

; 

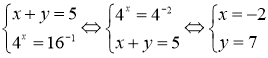Відповідь: Б

 

Завдання 3.

 

; 

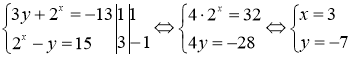Відповідь: А

 

Завдання 4.

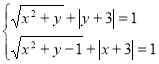.  Зауважимо, що з другого рівняння випливає: (область визначення), тому у першому рівнянні (множина значень). Але за умовою , тому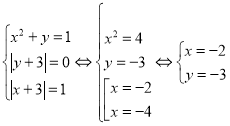

Відповідь:

 

Завдання 5.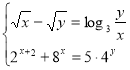

 

              Перше рівняння  для  перетворимо таким чином: 

       .  Функція зростає для , тому з умови     маємо: .  Отже,

 

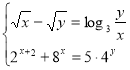
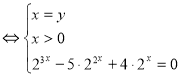
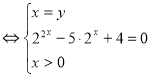
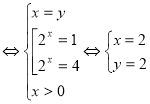
Відповідь:

 

ІІІ.  Обговорення теми уроку: Нестандартні методи розв’язування систем рівнянь (11 хв.)

 

1. Мотивація пізнавальної діяльності учнів.

        Одним із етапів навчального процесу, таким собі підсумком здобутого за 11 років, є ЗНО  (зовнішнє незалежне оцінювання). У 2010 році останнім, найбільш складним на думку авторів, було розміщено таке завдання:

                

 Чи можемо ми застосувати стандартні методи розв’язування систем до виконання цього завдання? Ні, бо перше рівняння можна віднести до класу нестандартних.

    А вже відомі нам нестандартні методи? На жаль, також – ні.

    Розглянемо рівняння, аналогічне за своєю нестандартністю першому рівнянню даної  

системи:

 

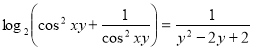          ; зауважимо, що за нерівністю Коші 

         і 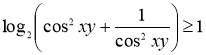, отже, найменше (мінімальне)

         значення цього виразу дорівнює 1 при ,  де  Z                                         (1)

  Розглянемо праву частину цього рівняння: , отже,

         найбільше (максимальне) значення цього виразу дорівнює 1 при                    (2)

                 За умовою значення лівої і правої частин збігаються, тому цей метод отримав назву

         Мінімакс;   порівняємо (1) і (2), отримємо розв’язок рівняння , де Z .

                Відповідь: , де Z                                       

 

 IV.  Застосування нових знань

    

1. Самостійна робота (2  етап)       https://forms.gle/egbrWu2bXbWwa5ni6

 

         

2. Самоперевірка робіт, заповнення карток накопичувальних балів (маршрутних листів)

 Для лівої частини першого рівняння:  , для правої частини першого рівняння:

. За умовою має виконуватися рівність

(мінімакс), отже, і  . Тоді з другого рівняння маємо . Залишилося переконатися у тому, що при значення виразу дорівнює 5:  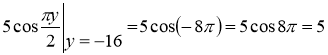. Маємо , отже .

Відповідь: ‒ 12

 

5. Інтелектуальна гра «Видатні науковці»

 

За 5 підказок треба визначити, хто цей науковець

         Правила: 1) правильна відповідь з першої підказки – 5 балів;

                          2) правильна відповідь з другої підказки – 4 бали і так далі;

                          3) правильна відповідь з останньої  підказки – 1 бал

Завдання 1.

        1)  Нам він відомий як французський математик, але за фахом він  юрист.

2. Захоплення астрономією спонукало його до  занять тригонометрією та алгеброю.     
3. Заочно був засуджений до смертної кари іспанською інквізицією за те, що знайшов

   ключ до шифру, який застосовували іспанці під час війни з Францією.

4. В його працях алгебра набуває статусу загальної науки про алгебраїчні рівняння, яка

      застосовує символи для позначень; за це його називають «батьком алгебри».

5. Усі школярі нашої країни у 8 класі вивчають його теорему про корені квадратного

рівняння. 

 

Правильна відповідь:

 

     Франсуа  Віет

 

 Завдання 2.

1. Цей середньоазійський математик, який написав трактат про розв’язування кубіч-

      них рівнянь, - справжній енциклопедист.

2. Коли він був керівником Ісфаханської астрономічої обсерваторії, працював над реформою іранського сонячного календаря.
3. Написав видатний математичний трактат «Коментарі до постулатів книги Евкліда».

      Один із небагатьох, хто брав під сумнів  необхідність V постулата Евкліда.

4. Написав твір «Терези мудрості», в якому розв’язав задачу Архімеда про визначення кількості золота і срібла в сплаві.
5. Паралельно з науковою роботою складав чудові вірші (рубаї):

« У кого кожний день в запасі пів коржа,

   У кого свій садок і хата не чужа,

   Хто в рабстві не родивсь і сам рабів не має,

   У того світлий зір і радісна душа»

                       (Переклад Василя Мисика)

 

 Правильна відповідь: ис. 2 

                                          

                        Омар Хайям

VI. Підведення підсумків гри

 

VIІ. Підведення підсумків уроку,  домашнє завдання

 

 1.  Отримати відповіді учнів на запитання:

             1) Чи отримали нову інформацію на уроці?

             2) Чи застосовували сьогодні такі властивості функцій, розв’язуючи рівняння та системи:

            2.1) область визначення

  2.2) множина значень

  2.3) монотонність

                     2.4) періодичність

                  2.5) екстремальні значення (мінімакс)

 

      2.  Оголосити оцінки учням за урок.

 3.  Оголосити домашнє завдання:

             1)  Опрацювати нестандартні методи  розв’язування систем (за конспектом);

        2)  розв’язати рівняння: 2.1) 2cos;  2.2)  log

        3)  розв’язати системи:  3.1) 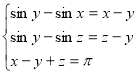   ;  3.2)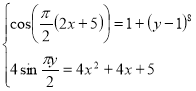 

    4.  Релакс (відео-любов)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

           Додатки

Картки накопичувальних балів або маршрутний лист (гугл-форма)

 

Дата		Прізвище, ім’я		Клас
Зміст роботи		Максимальний бал	Кількість балів
СР - 1	№1	1
	№2	2
	№3	2
	№4	2
	№5	2
СР - 2	№1	2
Гра		1
Додаткові бали
Всього