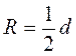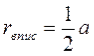Конспекти уроків геометрії у 8 класі. Розробка теми « Вписані та центральні кути.Теорема Фалеса."

Про матеріал

Конспекти уроків геометрії у 8 класі. Розробка теми « Вписані та центральні кути. Теорема Фалеса." Містить усі уроки теми, підсумкові уроки, самостійну та контрольні роботи.

Перегляд файлу

Конспекти уроків геометрії у 8 класі. Розробка теми «Теорема Фалеса. Вписані та центральні кути.

Підготувала Котис О.В.

вчитель математики

Городницької ЗОШ І-ІІ ст..

Скалатської міської ради

Підволочиського району

Урок 11.

Тема. Аналіз контрольної роботи. Теорема Фалеса

Мета: формувати в учнів усвідомлене розуміння змісту теореми Фалеса та способу її доведення; формувати вміння відтворювати формулювання теореми Фалеса; застосовувати її для розв'язування задач на знаходження довжин відрізків, що відтинаються на сторонах паралельними прямими; розв'язувати задачі на поділ відрізка на п рівні відрізки або в даному відношенні.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: конспект «Теорема Фалеса».

Хід уроку

І. Аналіз контрольної роботи.

IІ. Актуалізація опорних знань

З метою підготовки учнів до свідомого розуміння та способу доведення теореми Фалеса слід активізувати знання і вміння учнів щодо ознак паралельності прямих, властивості паралельних прямих, означення та властивостей паралелограма, ознак рівності трикутників.

Які прямі називаються паралельними?
Назвати властивості паралельних прямих.
Сформулювати ознаки рівності трикутників
Назвати властивості паралелограма.

Виконання усних вправ за готовими рисунками

Дано: 1 = 2.

Довести: 3 + 4 = 180°

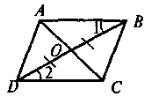
Дано: ВО = ОD, 1 = 2. Довести: ΔAOD = ΔCOB

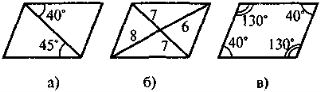
Які помилки допущено в зображенні паралелограма

ІІІ. Засвоєння знань

План вивчення нового матеріалу

«Класичне» формулювання і доведення теореми Фалеса.
інше формулювання теореми Фалеса.
Задача про поділ відрізка на п рівних частин.
Історична довідка

Фалес Мілетський (624-548рр.до н.р.) мав титул одного із семи мудреців Греції, він насправді був першим філософом, першим математиком, астрономом й, взагалі, першим по всіх науках у Греції. виміряв висоту Єгипетської піраміди за довжиною власної тіні.


Теорема Фалеса
	Паралельні прямі, які перетинають дві інші сторони кута і відтинають на одній із них рівні відрізки, відтинають рівні відрізки і на іншій стороні

Вважають, що Фалесу належить перше доведення теореми про рівність кутів при основі рівнобедреного трикутника, рівність вертикальних кутів і теореми, яку ми сьогодні вивчимо та використаємо при розв’язуванні задач.

Доведення теореми учнями по групах

Вчитель дає підказки на кожну групу

Проведіть пряму паралельну до прямої А
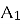
Розгляньте фігури, які при цьому утворилися та згадайте їх властивості.
Доведіть рівність утворених трикутників.
Доведіть рівність відрізків на сторонах кута.

Виконання усних вправ

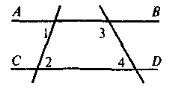
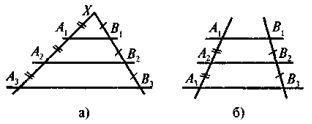
Дано кут х і прямі АА₁, ВВ₁, СС₁. Заповніть порожні клітинки таблиці: «+» означає виконання умови; «-» означає, що умова не виконується.

	АА₁ \|\| ВВ₁ \|\| СС₁	АА₁, ВВ₁ і СС₁ перетинають ХА	АА₁, ВВ₁ і СС₁ перетинають ХА₁	АВ = ВС	А₁В₁= В₁С₁
1	+	+	+	+
2	+	+	-	+
3	-	+	+	+
4		+	+	-	+

IV. Формування первинних умінь

Виконання письмових вправ

За даними рисунка 4 знайдіть х, якщо а || b.
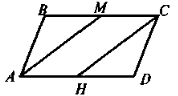
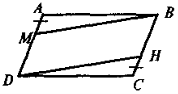
Точки М і N — середини сторін ВС і AD паралелограма ABCD. Доведіть, що прямі AM і CN ділять діагональ BD на три рівні частини.
Поділіть даний відрізок на шість рівних частин.
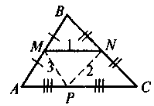
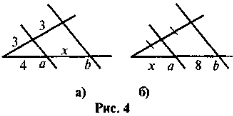
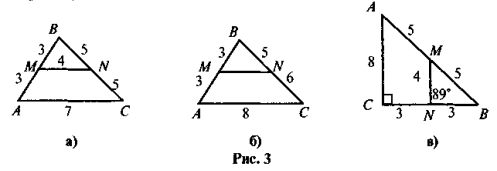
Точка К — середина медіани AD трикутника ABC (рис. 5). Знайдіть відношення АР : РС.

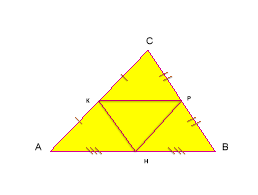
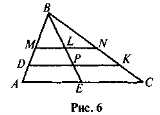У прямокутному трикутнику ABC (рис. 6) 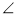B = 90°, АС = 24 см. МN || АС і DK || AC, ВМ = MA, MD = DA, BE – медіана. Знайдіть LP.

Виконання графічних вправ

Поділіть відрізок у відношенні: а) 1 : 2; б) 2 : 5; в) так, щоб одна з частин становила відрізка.

VII. Підсумки уроку

Чи правильне твердження: прямі, що відтинають на одній стороні кута рівні відрізки, відтинають на другій його стороні також рівні відрізки?

VIII. Домашнє завдання

Урок 12.

Тема. Середня лінія трикутника

Мета: сформувати в учнів поняття середньої лінії трикутника. Розглянути властивості середньої лінії трикутника та зміст задачі Вариньйона; формувати в учнів уміння: відтворювати вивчені твердження (означення та властивості); виконувати зображення середніх ліній трикутника та здійснювати доведення або спростування того, що даний відрізок є середньою лінією трикутника; відтворювати доведення властивості середньої лінії трикутника та опорної задачі; використовувати властивість середньої лінії трикутника під час розв'язування задач.

Тип уроку: засвоєння знань, умінь та навичок.

Наочність та обладнання: конспект «Середня лінія трикутника».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Практична робота

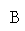Накресліть відрізок АВ. Поділіть даний відрізок на 5 рівних частин (Поділіть даний відрізок натри рівні частини)

Знайдіть відрізок х за рисунком. А

якщо АК=4см, КС=4см,

ВМ=3см, МС=хсм.

III. Формулювання мети і завдань уроку

Учитель повідомляє учням про те, що розв'язанням задачі на поділ даного відрізка на п рівних частин не обмежується практичне застосування теореми Фалеса. На уроці учні мають засвоїти одне з понять, властивості якого доводяться саме через застосування теореми Фалеса. Засвоєння означення, властивостей та способів застосування цього поняття для розв'язування задачі — головна мета уроку.

IV. Актуалізація опорних знань

З метою підготовки учнів до сприйняття нового поняття та подальшого оволодіння учнями способами дій на застосування нових знань слід активізувати знання і вміння учнів щодо поняття середини відрізка, означення трикутника та його елементів, поняття периметра многокутника, теореми Фалеса, ознак паралелограма.

Виконання усних вправ

1		Знайдіть на рисунку відрізки, які є одночасно сторонами не менш як трьох різних трикутників. Назвіть ці трикутники. Чи існують відрізки, які є одночасно сторонами не більш як двох трикутників, зображених на рисунку?
2		За рисунком складіть задачу і розв'яжіть її
3		Дано: M + В = 180°, M + A = 180°. Довести: АМВН - паралелограм
4		Дано: ABCD — паралелограм, М — середина ВС, Н — середина AD. Довести: АМСН — паралелограм
5		Дано: ABCD — паралелограм, AM = СН. Довести: DHBM — паралелограм

V. Засвоєння нових знань

План вивчення нового матеріалу

Означення середньої лінії трикутника.

Чи є зображена на рис. 1 лінія середньою лінією трикутника ABC?

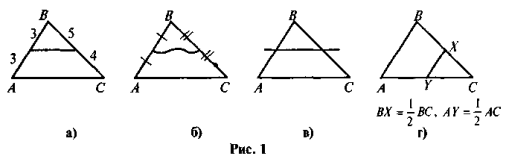
Властивості середньої лінії трикутника.


Середня лінія трикутника
	Означення. Середньою лінією трикутника називається відрізок, який сполучає середини двох його сторін.

Властивості
1. У будь-якому трикутнику можна провести 3 середніх лінії. 2. Якщо MN — середня лінія ΔАВС (М — середина АВ, N — середина ВС), то MN \|\| AC, MN = AC.
3. Периметр трикутника, утвореного всіма середніми лініями трикутника, дорівнює половині периметра даного трикутника (Р_Δ_MNP =Р_Δ_A_ВС).
4. Три середні лінії трикутника ділять його на чотири рівних трикутники

VI. Формування первинних умінь

Виконання усних вправ

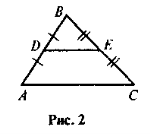
Відрізок DE — середня лінія трикутника ABC (рис. 2).

а) Визначте вид чотирикутника ADEC.

б) Назвіть медіану трикутника, що виходить з вершини А.

Чи може середня лінія трикутника бути перпендикулярною до його сторони; до двох його сторін?
Чи можуть середні лінії трикутника дорівнювати 3 см, 4 см і 10 см? Чому?
У трикутнику ABC проведено середню лінію паралельно стороні АС. У якому відношенні вона ділить медіану ВМ; висоту ВH?
Дві середні лінії трикутника рівні між собою і взаємно перпендикулярні. Який це трикутник? Відповідь поясніть.

Виконання графічних вправ

Накресліть трикутник ABC. Позначте на стороні АВ точки А₁, А₂і А₃так, щоб вони ділили відрізок АВ на чотири рівні частини. Проведіть через ці точки прямі, паралельні стороні АС, і позначте точки їх перетину зі стороною ВС С₁,С₂ і С₃ відповідно.

а) Виміряйте і порівняйте довжини відрізків, на які точки С₁,С₂ і С₃ ділять сторону ВС.

б) Виділіть червоним кольором середню лінію трикутника ABC.

Виконання письмових вправ

Сторони трикутника дорівнюють 12 см, 16 см і 20 см. Знайдіть сторони трикутника, вершинами якого є середини сторін даного трикутника.
Середня лінія трикутника відтинає від нього трапецію з бічними сторонами 3 м і 4 с і меншою основою 5 м. Знайдіть периметр трикутника.
Доведіть, що середини сторін ромба є вершинами прямокутника.

VII. Підсумки уроку

Які помилки допущено в зображенні середньої" лінії трикутника (див. рис. 3)?

VIII. Домашнє завдання

Вивчити зміст нового теоретичного матеріалу. Розв'язати задачі.

Накресліть трикутник ABC. Позначте точки D, Е і F — середини
сторін АВ, ВС і АС відповідно. Сполучіть позначені точки.

а) Визначте вид чотирикутника ADEF.

б) Визначте вид чотирикутника ADEC.

в) Назвіть усі трикутники, що дорівнюють трикутнику DEF. Запишіть відповідні рівності.

Середня лінія рівностороннього трикутника дорівнює 3,5 см. Знайдіть периметр трикутника.
Діагоналі чотирикутника дорівнюють 18 см і 22 см. Знайдіть периметр паралелограма, вершинами якого є середини сторін даного чотирикутника.
Доведіть, що середини сторін прямокутника є вершинами ромба.

Урок 13

Тема: «Середня лінія трикутника. Теорема про медіани трикутника.

Мета уроку: Перевірка знання учнів та вміння розв’язувати задачі.

Розвивати увагу учнів, наполегливість, логічне мислення, математичну мову.

Виховувати поважне ставлення одне до одного, прививати вміння уважно слухати інших, самостійність.

Хід уроку:

Перевірка домашнього завдання

(Поділити відрізок на 3 і на 4 рівних частини ( 2 учні біля дошки)
Інтерактивна технологія «Розгадай ребус».

Розгадай ребус

5 5 9 4 5 4 6 6 5 3 4 – ПРЯМОКУТНИК

1 5 6 6 5 5 4 6 6 5 3 4 – ГОСТРОКУТНИК

3) 1 3 2 5 3 3 5 4 – ВІДРІЗОК

4) 6 5 3 4 6 6 5 3 4 - ТРИКУТНИК

5) 5 5 9 4 1 – ПРЯМА

Шифр до ребусу:

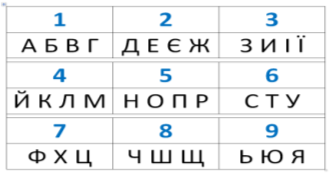
Відповідь: РОЗУМ

ІІ. Розв’язування вправ

Розв’язування усних задач

Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного.
Сторони трикутника, утвореного середніми лініями даного трикутника дорівнюють 4 см, 6 см і 8 см. Знайдіть периметр трикутника даного трикутника.
№ 294 ( ст. 61. Істер О.С.)

Розв’язання у зошиті задач

№ 297- 305.

Розглянути проблему.

З’єднавши послідовно середини сторін паралелограма отримали паралелограм

З’єднавши послідовно середини сторін квадрата отримали квадрат

З’єднавши послідовно середини сторін прямокутника отримали ромб

З’єднавши послідовно середини сторін ромба отримали прямокутник

З’єднавши послідовно середини сторін трапеції отримали паралелограм

З’єднавши послідовно середини сторін рівнобічної трапеції отримали ромб

Від чого залежить вид отриманого чотирикутника?

Теорема Медіани трикутника перетинаються в одній точці, яка ділить кожну медіану у співвідношені 2: 1, рахуючи від вершини

Підсумок уроку. Оцінювання
Домашнє завдання Повт. П.9-10. № 301, 303.

УРОК № 14

Тема уроку. Трапеція. Середня лінія трапеції, її властивості.

Мета уроку: увести поняття «середня лінія трапеції», довести теорему про властивість середньої лінії трапеції; формувати вміння розв'язувати задачі, застосовуючи теорему про середню лінію трапеції.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання

Учитель збирає зошити з домашньою роботою.

III. Формулювання мети і задач уроку

IV. Актуалізація опорних знань учнів

Питання класу

Сформулюйте означення трапеції.
Які сторони трапеції називаються основами?
Що називається середньою лінією трикутника?
Сформулюйте властивість середньої лінії трикутника.

V. Вивчення нового матеріалу

План викладення теми

Означення трапеції, її видів.
Означення середньої лінії трапеції.
Формулювання та доведення теореми про середню лінію трапеції.

Означення середньої лінії трапеції

Учитель формулює означення середньої лінії трапеції і дає учням завдання: зобразити трапецію ABCD і її середню лінію — відрізок MN.

Питання класу

Як розташована середня лінія трапеції відносно її основ?

Теорема про середню лінію трапеції

Для визначення довжини середньої лінії можна запропонувати виміряти довжини основ і порівняти їх півсуму з довжиною середньої лінії. Для підтвердження припущень щодо властивостей середньої лінії трапеції вчитель пропонує довести відповідну теорему двома способами.

Теорема. Середня лінія трапеції паралельна основам і дорівнює їх півсумі.

Одним із способів учитель доводить теорему сам, другим способом учні доводять її самостійно.

VI. Первинне закріплення нових знань учнів

Виконання усних вправ

Основи трапеції дорівнюють 5 см і 9 см. Чому дорівнює середня лінія трапеції? (Відповідь: 7 см.)
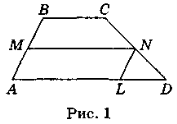
Відрізок MN — середня лінія трапеції ABCD (рис. 1). Через точку N проведено пряму, яка паралельна стороні АВ і перетинає сторону AD у точці L. Доведіть, що AMNL — паралелограм.
У трапеції ABCD АВ = 4 см, ВС = 6 см, CD = 5 см, AD = 10 см, MN — середня лінія. Чому дорівнюють сторони трапеції AMND1 (Відповідь: 2 см; 8 см; 2,5 см; 10 см.)
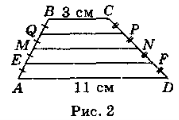
Кожну з бічних сторін трапеції ABCD (AD || BC) розділено на чотири рівні частини (рис. 2). Чому дорівнюють відрізки EF, MN і QP, якщо AD = 11 см, BC = 3 см? (Відповідь: EF = 9 см; MN = 7 см; QP = 5 см.)
Середня лінія трапеції дорівнює 8 см, а одна з основ — 6 см. Знайдіть другу основу трапеції. (Відповідь: 10 см.)

Виконання письмових вправ

Середня лінія трапеції дорівнює 24 см. Основи трапеції відносяться як 3 : 5. Знайдіть основи трапеції. (Відповідь: 18 см; 30 см.)
Основи трапеції дорівнюють 8 см і 14 см. Знайдіть відрізки, на які діагональ ділить середню лінію трапеції. (Відповідь: 4 см і 7 см.)
Більша основа трапеції дорівнює 8 см, а менша основа на 3 см є меншою від середньої лінії. Знайдіть меншу основу та середню лінію трапеції. (Відповідь: 2 см, 5 см.)
У трапеції ABCD бічна сторона АВ перпендикулярна до основ, а бічна сторона CD дорівнює діагоналі АС. Знайдіть середню лінію трапеції, якщо ВС = 1 м. (Відповідь: 1,5 м.)
У рівнобічній трапеції діагональ є бісектрисою гострого кута, одна з основ на 6 см більша від іншої. Знайдіть середню лінію трапеції, якщо її периметр дорівнює 74 см.

Розв'язання

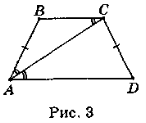
Нехай ABCD (рис. 3) — рівнобічна трапеція (AB = CD), AC — бісектриса кута А. Нехай ВС = х см (х > 0), тоді (х + 6) см — нижня основа трапеції. Оскільки BAC = CAD і BC || AD, a AC — січна, то BCA = CAD, і отже, трикутник ABC рівнобедрений з основою АС. Таким чином, AB = BC = CD = x см. Тоді за умовою P_ABCD = x + x + x + x + 6 = 74, 4x = 68, х = 17. Отже, ВС = 17 см, AD = 17 + 6 = 23 (см). Таким чином, середня лінія трапеції дорівнює (см).

Відповідь: 20 см.

Бічна сторона рівнобічної трапеції дорівнює 18 см, а більша основа — 32 см. Кут між ними дорівнює 60°. Знайдіть середню лінію трапеції.

Розв'язання

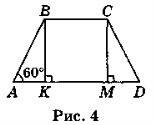Нехай ABCD (рис. 4) — рівнобічна трапеція, АВ = CD = 18 см, AD = 32 см, BAD = 60°. Із вершин В і С трапеції проведемо висоти ВК і CM (BK AD, CM AD). Тоді у трикутнику АВК АК = АВ = 9 см (як катет, який лежить проти кута в 30°). Отже, і MD = 9 см. Тоді KM = AD – 2AK = 32 – 18 = 14 (см). Звідси ВС = КМ = = 14 см. Отже, середня лінія трапеції ABCD дорівнює (см).

Відповідь: 23 см.

VII. Підбиття підсумків уроку

Питання класу

Який відрізок у трапеції називається її середньою лінією?
Сформулюйте властивість середньої лінії трапеції.
Чи може середня лінія трапеції дорівнювати одній з основ?

VIII. Домашнє завдання

С 1. Чи може середня лінія трапеції бути: а) у 2 рази більшою, ніж менша основа? б) у 2 рази меншою, ніж більша основа?

С 2. Середня лінія трапеції дорівнює 11 см, а менша основа — 6 см. Знайдіть більшу основу трапеції.

Д 3. Більша основа трапеції відноситься до середньої лінії як 5:4. Середня лінія більша за меншу основу на 5 см. Знайдіть основи трапеції.

Д 4. Діагональ АС ділить прямокутну трапецію ABCD на два трикутники — прямокутний і рівносторонній. Знайдіть середню лінію трапеції, якщо її більша основа дорівнює 12 см.

В 5. У прямокутній трапеції ABCD (BC||AD) діагональ АС є перпендикулярною до бічної сторони CD і ділить кут А у відношенні 2:1 починаючи від вершини більшої основи. Знайдіть середню лінію трапеції, якщо АС = 14 см.

В 6. У рівнобічній трапеції з гострим кутом 60° бісектриса цього кута ділить меншу основу навпіл. Знайдіть середню лінію трапеції, якщо менша основа дорівнює 16 см.

Урок № 15

Тема: Розв’язування задач. Самостійна робота.

Мета: розвивати в учнів поняття середньої лінії трапеції; працювати над засвоєнням змісту властивості середньої лінії трапеції, а також схеми її доведення. Формувати в учнів уміння: відтворювати зміст вивчених на уроці тверджень; виконувати зображення середньої лінії трапеції; використовувати властивість середньої лінії трапеції для розв'язування задач; використовувати вивчену властивість у комплексі з раніше вивченими властивостями трапеції.

Тип уроку: засвоєння нових знань.

Наочність та обладнання: таблиця.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

усне бліцопитування

Сформулюйте теорему Фалеса.

Що таке середня лінія трикутника?
Яка залежність між периметром даного трикутника та трикутника утвореного його середніми лініями?
Сформулюйте властивості середньої лінії трикутника.
Чи можна побудувати в трикутнику 4 середні лінії? Поясніть.
Якщо всі середні лінії трикутника рівні, то яким буде цей трикутник?
Дайте означення трапеції.
Які види трапеції ви знаєте?
Що таке середня лінія трапеції?
Сформулюйте властивість середньої лінії трапеції.
Хто (за думкою істориків) почав застосовувати основні геометричні інструменти – циркуль і лінійку?

ІІІ. Мотивація

Прийом « Проблемне запитання»

Учитель: Як ви вважаєте, чи можна на практиці, не застосовуючи безпосередню вимірювання, а використовуючи тільки знання з геометрії, визначити довжину або ширину заболоченого місця?

І на це питання нам в кінці уроку дасть відповідь один учень, якому ця задача задавалась, як індивідуальне домашнє завдання.

ІV. Закріплення і застосування навичок та вмінь

Розв’язування задач. Для цього ви об’єднаєтесь парами і розв’язавши задачі ви довідаєтесь, як називається наука, яка є однією із найдавніших математичних наук.

Це наука про визначення форми і розмірів Землі, про вимірювання на земній поверхні для відображення її на планах і картах.

Номер завдання, це порядковий номер у загадковому слові. Кожна пара отримує по 2 завдання, тобто може розгадати дві букви в слові. Розгадка всього слова залежить від роботи всього класу, як команди.

Під час виконання даного завдання учням пропонується фізкультхвилинка. А саме

Картка 1.

Відповідь: 40см.

Картка 2

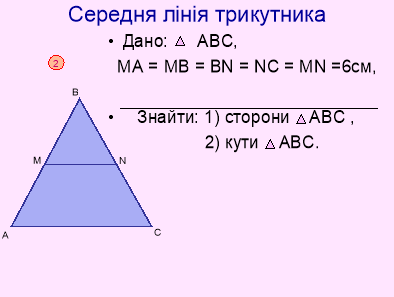
Відповідь: рівносторонній трикутник; 60⁰.

Картка 3.

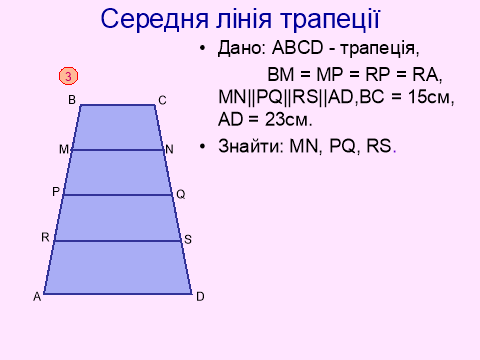
Відповідь: 17см, 19см, 21см.

Картка 4.

Відповідь: 10см

Картка 5. Задача практичного змісту« Практичність теорії »

Умова задачі:

Над входом у дачний будинок є навіс. Згодом виникла потреба поставити підпори до середини навісу (точка Fна малюнку 176). Як, не вимірюючи, знайти довжину підпори (відрізка EF), якщо відповідні краї навісу віддалені від поверхні землі на 2,5 м і 3,5 м? Подумайте, поміркуйте і зробіть геометричний малюнок до цієї задачі так, щоб за готовим кресленням ми могли розв’язати задачу

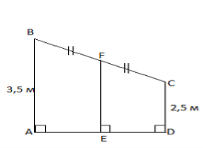
$H:\к задаче 4.png$

мал.4

1.Учні пояснюють, чому саме такий малюнок(чому треба зобразити прямокутну трапецію,чому FE – середня лінія).

2.Обчислюють довжину підпори FE, як довжину середньої лінії трапеції.

FE = (2,5+3,5)/2.

Відповідь: довжина підпори 3 метри

Картка 6. Задача практичного змісту« Практичність теорії »

Робота з підручником №335, ст.. 60

Умова задачі:

Знайдіть відстань від кінця транспортера до поверхні землі (яку безпосередньо виміряти не можна), якщо другий його кінець і середина віддалені від поверхні землі відповідно на 0,5 м і 2 м (малюнок 180).

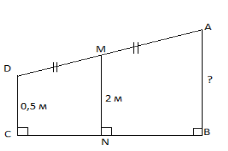
$H:\к задаче 5.png$

мал.4

1.Учні пояснюють, чому треба зобразити прямокутну трапецію, спираючись на поняття відстані.

2.Доводять, що MN – середня лінія, використовуючи теорему Фалеса3.Знаходять відстань від кінця транспортера до поверхні землі,як довжину основи ABтрапеції ABCD:AB = 2*2 – 0,5.

Відповідь:3,5 метри.

Картка №7.

Робота з підручником

Умова задачі: Знайдіть периметр трикутника, якщо його середні лінії дорівнюють: 8см, 10см, 12см.

Розв’язання:

1)8∙2=16 (см)- одна сторона трикутника дорівнює;

2)10∙2=20(см)- друга сторона трикутника дорівнює;

3) 12∙2=24(см) - третя сторона трикутника;

4) Р=16+20+24=60(см).

Відповідь: 60см.

Картка №8.

Робота із збірником Умова задачі: Периметр трикутника дорівнює 68см, а довжини його середніх сторін відносяться як 4:6:7. Знайдіть сторони даного трикутника.

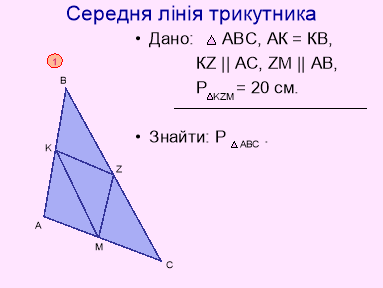
Дано:

∆АВС;

М-середина АВ;

К-середина ВС

Р-середина АС;

Р_АВС=54см;

КР:РН:КН=4:6:7

Знайти АВ,ВС,АС.

Розв’язання

Р=68:2=34(см)-вл.середньої лінії трикутника;

Введемо коефіцієнт пропорційності –х. Тоді:

4х+6х+7х=34

17х=34

х=34:17

х=2.

отже:

АВ=4∙2∙2=16см;

АС=6∙2∙2=24см;

ВС=7∙2∙2=28см.

Відповідь: 16см, 24см, 28см.

Дешифратор слова:

Г	Е	О	Д	Е	З	І	Я
1	2	3	4	5	6	7	8

Відповідь	Буква слова
Паралелограм	К
18см, 40см, 66см	Т
Рівнобедрений, 60⁰	С
16см, 24см, 28см.	Я
30см	Г
60см	А
10см	Д
Рівносторонній, 60⁰	Е
17см, 19см, 21см.	О
30см²	Л
60см	І
3м	Е
7см	Н
3,5м	З
Прямокутник	Д
40см	Г

Учням роздаються бланки, які вони заповнюють.

Номер картки – це номер букви в слові	Буква в слові

Учні маркером вписують відгадані букви. Якщо розв’язали правильно, то повинні отримати слово «геодезія».

Геоде́зія (грец. γεωδαισια) наука про методи визначення фігури і розмірів Землі,

зображення земної поверхні на планах і картах і точних вимірювань на місцевості, пов'язаних з розв'язанням різних наукових і практичних завдань.

Геодезія тісно пов'язана з математикою,фізикою,радіоелектронікою,

радіотехнікою,геофізикою,астрономією, картографією,географією,

геоморфологією,геоінформатикою.

Є професії, які вимагають дуже часто розв'язувати трикутники. Насамперед цим займаються геодезисти. Яке б велике будівництво не розпочиналось, першими туди йдуть геодезисти, щоб зняти план місцевості та охарактеризувати рельєф. Коли ж на основі їх матеріалів у проектних організаціях опрацюють проект, геодезисти знову міряють кути, розв'язують трикутники, забивають кілочки — «прив'язують» опрацьований проект до місцевості. (слайд №15)

А тепер повернемось до нашої задачі. « Практичність теорії »

Учень, якому ця задача була на домашнє опрацювання виходить до дошки і пояснює її розв’язання(умова задачі попередньо замальована на відкидній дошці або ватмані).

На мал. зображено заболочене місце. Добудуємо прямі ОР, ОF та РF, що виходять з довільної точки О.

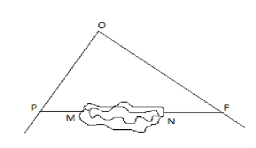
$H:\to task 3.png$

1.Виміряємо ОР,ОF,знайти середини цих відрізків,виміряти довжину середньої лінії трикутника РОF

2.Обчислити відстань між пунктами Р та F,як основу трикутника використовуючи властивість середньої лінії.

3.Виміряти відстані РМ і NF. Протяжність заболоченого місця обчислити за формулою МN=PF-(PM+NF).

Додаткове завдання(за рахунок вільного часу, або для учнів, які вже виконали завдання по картках). Конверти з прямокутними трикутниками і завданням роздаються учням.

ЦІКАВА ЗАДАЧА

Скласти трапецію з:

а) чотирьох прямокутних трикутників;

б) із трьох прямокутних трикутників;

в) із двох прямокутних трикутників.

V.Підбиття підсумків уроку.

Як на вашу думку, знання із даної теми знайдуть практичне застосування у майбутньому вашому житті?

Чи задоволені ви своєю роботою на уроці?

Сподіваюся що на цьому уроці ви ще раз переконалися у справедливості відомого висловлювання:«Геометрія навколо нас». І маю надію що при нагоді вам вдасться скористатися знаннями здобутими на уроках геометрії,принаймні мені б цього дуже хотілося.

Оцінюються учні враховуючи їх усні відповіді, розв’язки задач і активність на уроці.

VІ.Домашнє завдання.

§9-11-повторити

Самостійна робота.

Самостійна робота №4 8 кл

Варіант 1

Поділіть даний відрізок на 5 рівних частин.
Діагональ трапеції ділить її середню лінію на два відрізки, які відносяться як 3:8. Знайдіть основи трапеції, якщо середня лінія трапеції дорівнює 22 см.
Сторони трикутника дорівнюють 6 см, 8 см і 10 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного.
Периметр трапеції дорівнює 22 см, а її бічні сторони — 4 см і 8 см. Знайти середню лінію трапеції.
Кут при більшій основі рівнобедреної трапеції дорівнює 60°. Її бічна сторона перпендикулярна до діагоналі і дорівнює 12 см. Чому дорівнює периметр даної трапеції?

Самостійна робота №4 8 кл

Варіант 2

Поділіть даний відрізок натри рівні частини.
Діагональ трапеції ділить її середню лінію на 2 відрізки, один з яких в 2 рази більший від другого. Знайдіть основи трапеції, якщо її середня лінія дорівнює 21 см.
Сторони трикутника дорівнюють 4 см, 6 см і 8 см. Знайдіть периметр трикутника, вершинами якого є середини сторін даного трикутника.
Бічна сторона рівнобічної трапеції дорівнює 6 см, а її периметр — 34 см. Знайти середню лінію трапеції.
Менша основа рівнобічної трапеції дорівнює її бічній стороні, а кут при більшій основі дорівнює 60⁰. Знайдіть периметр трапеції, якщо її більша основа 15 дм.

Урок № 16

Тема. Вписані та центральні кути

Мета: домогтися засвоєння учнями змісту понять: плоский кут (у неявному вигляді), центральний кут, дуга кола, що відповідає даному центральному куту, градусна міра дуги кола, вписаний кут, — а також засвоєння учнями змісту властивості вписаного кута (про вимірювання вписаного кута). Формувати вміння: відтворювати зміст вивчених тверджень; знаходити на готовому рисунку вивчені поняття; виконувати правильні зображення вивчених понять заданим описом; розв'язувати задачі із використанням вивчених тверджень на обчислення градусної міри вписаних та центральних кутів.

Тип уроку: застосування знань, умінь та навичок.

Наочність та обладнання: таблиця.

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання

Перевірка правильності виконання письмової частини домашнього завдання відбувається під час перевірки зошитів із виконаною домашньою роботою.

ІІІ. Формулювання мети і завдань уроку

IV. Актуалізація опорних знань

Дати означення кута
Які види кутів ви знаєте? За яким принципом класифікуються кути?
Зобразити кілька кутів різного виду й зазначити відмінність між ними?

V. Засвоєння вмінь та навичок

План вивчення нового матеріалу

Розширення поняття кута.

Центральний кут: означення, вимірювання.

Градусна міра дуги.

Означення вписаного кута. Дуга, на яку спирається вписаний кут.

Теорема про вписаний кут: формулювання і доведення.

за записаним вище планом.

Виконання усних вправ

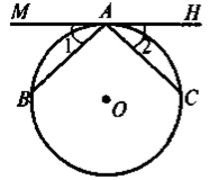
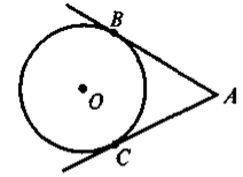
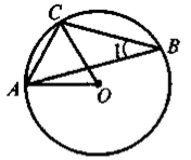
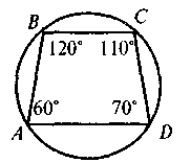
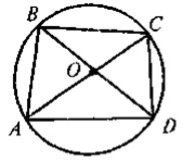
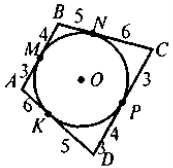
На кожному з рисунків знайдіть та назвіть:

а) центральний кут;

б) дугу, що відповідає центральному кугу;

в) вписаний кут, що спирається на цю дугу.

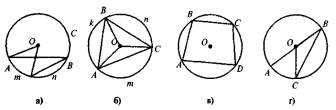
Виконання графічних вправ

Накресліть коло із центром і позначте на ньому точки А, В і С.

а) Виділіть двома кольорами доповняльні плоскі кути, утворені променями ОА і ОС.

б) Яким кольором виділено кут, що вдвічі більший за кут ABC?

в) Позначте на колі точку D так, щоб вписані куги ABC і ADC були рівні.

Виконання письмових вправ

Знайдіть доповняльні плоскі кути, якщо:

а) один з них більший за інший на 120°;

б) їх градусні міри відносяться як 2:7.

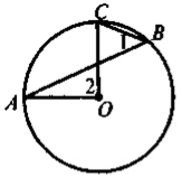
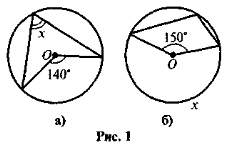
За даними рисунка 1 знайдіть градусну міру х (точка О — центр кола).

На колі позначено точки А, В, С і D. Знайдіть кут ABC, якщо ADC = α. Скільки розв'язків має задача?

VІ. Робота з підрічником

№234 – біля дошки,

№ 236, 238 – робота в групах.

№ 240 – робота в парах

VII. Підсумки уроку

VIII. Домашнє завдання

Вивчити зміст теоретичних тверджень та доведення теореми про вписаний кут.

§7, № 232, 235, 241.

Урок № 18

ТЕМА. Вписані та описані чотирикутники.

Мета: сформувати поняття чотирикутника, вписаного в коло, та чотирикутника, описаного навколо кола; домогтися засвоєння властивостей кутів вписаного та сторін описаного чотирикутників; домогтися розуміння умов, за якими чотирикутник є вписаним або описаним. Розвивати графічні здібності, математичну мову, обчислювальні навички. Виховувати культуру спілкування на уроці.

Тип уроку: засвоєння нових знань і вмінь.
Обладнання та наочність: таблиця.

ХІД УРОКУ

І. Організаційний етап.

II. Аналіз контрольної роботи.

III. Актуалізація опорних знань.

Запитання для фронтальної бесіди

1. На якому з наведених рисунків зображено:

а) трикутник, вписаний у коло;

б) трикутник, описаний навколо кола;

в) коло, описане навколо трикутника;

г) коло, вписане в трикутник?

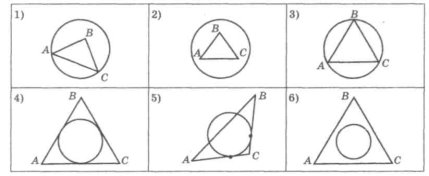
IV. Вивчення нового матеріалу

План вивчення теми

Означення вписаного чотирикутника.
Властивість кутів вписаного чотирикутника.
Умова, за якою чотирикутник є вписаним.
Означення описаного чотирикутника.
Властивість сторін описаного чотирикутника.
Умова, за якою чотирикутник є описаним.

V. Закріплення нових знань і вмінь

1. Робота з підручником: № 252, 254, 256 – робота в групах (1), (2)

№ 258, 262 – біля дошки.

VI. Підбиття підсумків уроку.

VII. Домашнє завдання.

Завдання за підручником: §8, № 253, 255, 259

Урок № 19

Тема. Вписані чотирикутники. Описані чотирикутники

Мета:працювати над засвоєнням учнями змісту понять: чотирикутник, вписаний у коло; чотирикутник, описаний навколо кола; розглянути зміст теорем про вписаний та описаний чотирикутники та схеми їх доведення.

Сформувати вміння:

· відтворювати вивчені твердження;

· виконувати рисунок за описом;

· використовувати вивчені теореми під час розв'язування теореми на чотирикутники.

Тип уроку: засвоєння знань, умінь та навичок.

Наочність та обладнання: конспект «Вписаний і описаний многокутники».

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

З метою економії часу перевірка домашнього завдання проводиться у формі бесіди за готовими рисунками (рисунки до домашніх задач учитель виконує на дошці заздалегідь; також можна записати схеми розв'язання задач). Бесіда проводиться під керівництвом учителя, який ставить питання на розуміння учнями обґрунтування основних етапів розв'язання задач.

III. Формулювання мети і завдань уроку

Учитель нагадує про складену на 20-му уроці схему, в якій відображено логіку викладення навчального матеріалу з теми «Чотирикутники». Після цього формулюється основна мета уроку — вивчення питання про спосіб визначення поняття чотирикутника, вписаного в коло та описаного навколо кола, з'ясування можливостей вписати чотирикутник у коло або описати чотирикутник навколо кола та необхідних й достатніх умов, за яких це можна зробити.

IV. Актуалізація опорних знань

Для успішного засвоєння учнями означення, властивості, ознаки та способів доведення теорем про вписаний та описаний чотирикутники слід активізувати знання і вміння учнів щодо означення та властивості дотичної до кола та наслідку з неї (властивість відрізків дотичних); теореми про бісектрису кута.

Виконання усних вправ за готовими рисунками

1		Дано: ВС — дотична, О — центр кола, АВ = АС. Довести: ОВ = ОС
2		Дано: О — центр кола, 1 = 45°. Знайти: кут 2
3		Дано: МН — дотична, 1 = 2. Довести: АВ = АС
4		Дано: О — центр кола, АВ і АС — дотичні. Довести: АВ = АС
5		Дано: О — центр кола, 1 = 30°. Довести: ΔАОС — рівносторонній

V. Засвоєння знань

План вивчення матеріалу

1. Означення чотирикутника, вписаного в коло.

2. Теорема про вписаний чотирикутник.

3. Наслідки з теореми про вписаний чотирикутник.

4. Означення описаною чотирикутника.

5. Теорема про описаний чотирикутник.

6. Наслідки з теореми про описаний чотирикутник.

Завдання.

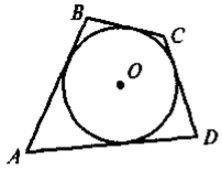
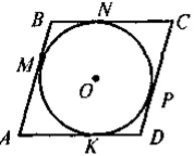
На якому із наведених рисунків зображено чотирикутник ABCD:

а) вписаний у коло;

б) описаний навколо кола?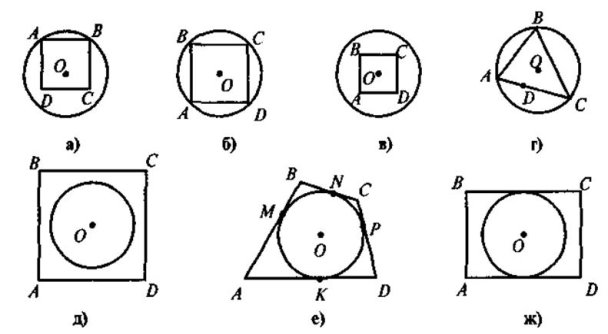

Для таких чотирикутників назвіть радіуси кіл(описаного або вписаного).

Виконання усних вправ

1. У який прямокутник можна вписати коло? Навколо якого ромба можна описати коло?

2. Чи можна описати коло навколо чотирикутника, який має лише один прямий кут; лише три прямі кути?

· Для практичних потреб найбільшу цінність мають наслідки з теорем про вписаний та описаний чотирикутники, а також опорні задачі.

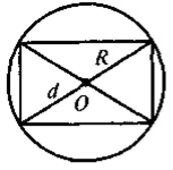
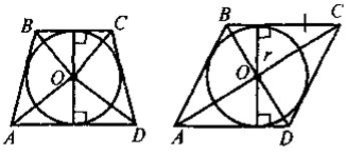
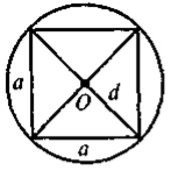
Задача 1. Центр кола, описаного навколо прямокутника, є точкою перетину його діагоналей.

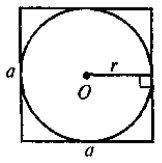
Задача 2. Центр кола, вписаного в ромб, є точкою перетину його діагоналей, а радіус кола дорівнює половині висоти ромба.


Вписаний і описаний многокутники (вписане і описане кола)

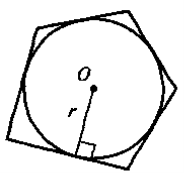
Вписаний — усі вершини лежать на колі	Описаний — усі сторони є дотичними до кола. , де Р — периметр, r — радіус вписаного кола
Вписаний та описаний чотирикутники

A + C = 180o, B + D = 180o І навпаки: якщо сума протилежних кутів чотирикутника дорівнює 180°, то навколо нього можна описати коло	AB + CD = BC + AD (суми довжин протилежних сторін рівні) І навпаки: якщо суми довжин протилежних сторін випуклого чотирикутника рівні, то в нього можна вписати коло
Прямокутник
	1. Якщо паралелограм вписано в коло, то він прямокутник. 2. Центр кола, описаного навколо прямокутника, — точка перетину діагоналей
Трапеція і ромб

Якщо ABCD — вписана трапеція, то AB= CD	d впиc. кола = h O — точка перетину бісектрис внутрішніх кутів. AOB = COD = 90°
Квадрат

VI. Формування первинних умінь

Виконання усних вправ

1. Чи можна описати коло навколо прямокутної трапеції?

2. У трапеції три сторони рівні. Чи можна в таку трапецію вписати коло? Чи можна навколо такої трапеції описати коло?

Виконання письмових вправ

1. Визначте, чи можна описати коло навколо чотирикутника ABCD, якщо кути А, В, С, D дорівнюють відповідно:

а) 90°, 90°, 20°, 160°; б) 5°, 120°, 175°, 60°.

2. Знайдіть невідомі кути:

а) вписаного чотирикутника, якщо два з них дорівнюють 46° і 125°;

б) вписаної трапеції, якщо один із них дорівнює 80°;

в) вписаного чотирикутника, діагоналі якого точкою перетину діляться навпіл.

3. Знайдіть периметр:

а) описаного чотирикутника, три послідовні сторони якого дорівнюють 7 см, 9 см і 8 см;

б) описаної трапеції, бічні сторони якої дорівнюють 3 см і 11 см.

4. Рівнобедрена трапеція описана навколо кола. Знайдіть середню лінію трапеції, якщо її бічна сторона дорівнює 7 см.

5. Діагональ ромба, що виходить з вершини кута 60°, дорівнює 24 см. Знайдіть радіус кола, вписаного в ромб.

VII. Підсумки уроку

Засвоєння учнями змісту основних тверджень перевіряємо під час Виконання завдання.

Які помилки допущено в зображенні чотирикутників (див. рис)?

а)	б) АВ = 5 см, ВС = 5,5 см

в) О — центр кола; ABCD - трапеція	г)

VIII. Домашнє завдання

Вивчити зміст теоретичного матеріалу. Виконати домашню самостійну роботу.

Домашня самостійна робота

1. У трикутнику ABC точки М і N — середини сторін АВ і ВС відповідно. Периметр трикутника ABC дорівнює 22 см. Знайдіть периметр трикутника MBN.

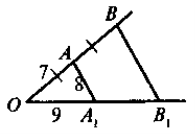
2. На рисунку ABB1 + A1AB = 180°. Знайдіть периметр чотирикутника АВВ1А1.

3. Знайдіть кути рівнобедреного трикутника, основа якого стягує п'яту частину дуги описаного кола. Розгляньте всі можливі випадки.

Урок 20

Тема уроку: Теорема Фалеса. Трапеція. Вписані та описані чотирикутники. Розв’язування задач.

Цілі уроку:

Навчальні: Повторити, систематизувати та узагальнити знання щодо:

означення, ознак та властивостей трапеції;
теореми Фалеса;
означення та властивостей кутів у колі;
означення вписаних та описаних чотирикутників, їх властивостей та ознак.

Повторити, систематизувати та узагальнити вміння застосовувати вивчені твердження для:

«читання задач - рисунків»;
побудови правильних міркувань під час розв’язування задач різних типів.

Розвивальні: розвивати пам’ять, логічне мисленнння учнів, формувати вміння аналізувати інформацію.

Виховні: виховувати дисциплінованість, самостійність, відповідальність за результати своєї роботи.

Очікувані результати: учні знають властивості трапеції, теорему Фалеса, властивості середньої лінії трикутника і трапеції, властивості кутів у колі, властивості вписаних і описаних чотирикутників та вміють використовувати їх під час розв’язування задач.

Тип уроку: узагальнення знань, умінь, навичок

Обладнання:

1. кросворд

2. картки математичного лото

3. комп’ютерна презентація за програмою Pоwer Point

4. індивідуальні завдання

5. тестові завдання

Епіграф уроку:

Серед рівних розумом – за однакових умов –

переважає той, хто знає геометрію.

Б. Паскаль

Девіз уроку:

Тільки після невтомної праці

з’явиться талант.

Народна мудрість

ХІД УРОКУ

І. Організаційний етап.

ІІ. Мотивація навчальної діяльності.

На попередніх уроках ми вивчили теорему Фалеса, види трапецій та їх властивості, середню лінію трикутника і середню лінію трапеції, означення та ознаки вписаних і описаних чотирикутників; навчилися використовувати вивчений матеріал при розв’язуванні задач. Мета сьогоднішнього уроку – повторити, узагальнити та систематизувати ці знання, і таким чином підготуватися до контрольної роботи.

І розпочати наш урок я хочу із казки «Пряник і Колосок», яку написав своєму сину відомий педагог В.О.Сухомлинський.

Вранці, до сходу сонця Людина взяла білий пряник і пішла в поле. Зірвала колосок у полі, вийняла з нього зернята, спробувала на зуб, посміхнулася і заховала колосок у кишеню. Ось там і зустрілися Пряник і Колосок.

Хто ти такий? – запитав Пряник.
Я – Колосок.
Ой, який ти колячий! Яка з тебе користь?

Посміхнувся Колосок, поворухнув своїми вусиками і відповів:

Без мене не було б ні хліба, ні сухаря, ні тебе, Прянику.
Отже, - каже Пряник, - все від тебе. Але хто ж над тобою старший?
Праця, - відповідає Колосок, - вона все дає. Але праця в руках людини. Праця і Людина – найголовніші.

Отже, я вас закликаю до праці, до праці наполегливої і творчої, щоб пізнавати істину міркувань. Народна мудрість говорить: «Тільки після невтомної праці з’явиться талант». Я думаю, що наш урок буде тому підтвердженням. І всі ми покажемо, які ми працьовиті, наполегливі і талановиті.

ІІІ. Актуалізація опорних знань.

Якщо немає запитань стосовно домашньої роботи, то я пропоную розв’язати аналогічні завдання біля дошки:

Індивідуальні завдання.

Задача 1.

Знайти довжину відрізка, що сполучає середини діагоналей трапеції, основи якої дорівнюють 6см і 14см.

Задача 2.

Три кути чотирикутника, вписаного в коло, узяті в порядку наступності, відносяться як 2:6:7. Знайти кути чотирикутника.

Питання до класу.

Який чотирикутник ми називаємо трапецією? Які види трапеції ви знаєте?
Чому дорівнює сереня лінія трапеції (трикутника)?
Які кути називаються вписаними у коло, а які центральними?
Сформулюйте властивості вписаних кутів.
В якому випадку чотирикутник можна вписати у коло, а в якому – описати навколо кола?

3. Опитування учнів біля дошки.

4. Усні вправи.

1. Знайти невідомий відрізок х(рис.1):

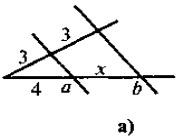
Рис. 1

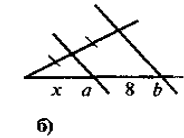
2.На якому із наведених рисунків зображено чотирикутник ABCD:

а) вписаний у коло;

б) описаний навколо кола?

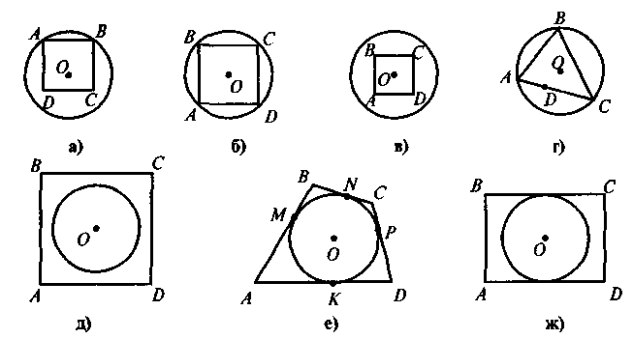
Рис.2

3. Знайдіть довжину відрізка х (рис. 3):

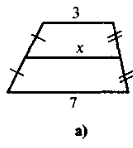
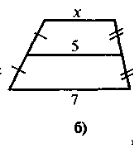
Рис.3

4. Знайдіть на рисунку 4 помилки (поясніть).

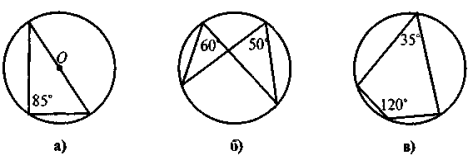
Рис.4

ІУ. Застосування знань і вмінь.

Розв’язування задач (колективна робота, готові малюнки на слайдах).

Задача 1

У рівнобічній трапеції діагональ є бісектрисою гострого кута, одна з основ на 6см більша від іншої. Знайти середню лінію трапеції, якщо її периметр дорівнює 74см.

Задача 2

Хорда АВ стягує дугу в 58⁰. Визначте кути, утворені хордою і дотичною, проведеною до кола в точці А.

У. Математичне лото.

І група Хто нічого не вивчає,

той завжди

скиглить і нудьгує.

Хто любить учитися,

той ніколи не проводить

час у ледарстві.

Ш.Монтеск’є

ІІ група Можливо, течія приведете тебе

зовсім не туди,

куди ти думаєш.

Що можеш зробити – зроби зараз,

хто знає, чи зможеш ти

це зробити потім.

Китайське прислів’я

ІІІ група Труднощі зростають із наближенням до мети.

Але нехай кожен робиь свій шлях

подібно до зірок –

спокійно, не поспішаючи,

але безперервно прагнучи

до наміченої мети.

Й.В.Гете

Не випадково ми саме ці слова вибрали для нашої гри. Адже цей тиждень у школі – це тиждень трудового навчання. І в цих крилатих висловах зібрана по-справжньому народна мудрість, яка закликає нас вчитися і працювати, старанно, систематично і наполегливо.

УІ. Завдання додому.

Повторити §4 - §7, підготуватися до контрольної роботи;

с.65 (задачі за готовими малюнками) №1(а), №2(б).

Додатково: №4(б).

VII. Підсумки уроку.

Таким чином ми повторили весь необхідний теоретичний матеріал та основні типи задач, що розглядаються в цьому розділі. Я думаю, що ще попрацювавши вдома ви належним чином підготуєтеся до контрольної роботи. А зараз з метою перевірки ваших знань та вмінь проведемо таку невелику тестову роботу із взаємоперевіркою.

Тестові завдання

І варіант ІІ варіант

1. Центральний кут у колі дорівнює

120⁰ 160⁰.

Тоді градусна міра відповідного вписаного кута становить:

А	Б	В	Г
80⁰	160⁰	120⁰	60⁰

Основа рівнобедреного трикутника дорівнює

18см 22см

Чому дорівнює середня лінія, паралельна цій основі?

А	Б	В	Г
18см	11см	9см	22см

Два послідовні кути вписаного чотирикутника дорівнюють

80⁰ і 120⁰ 60⁰ і 100⁰.

Знайти два інші кути.

А	Б	В	Г
120⁰ і 80⁰	140⁰ і40⁰	120⁰ і 60⁰	100⁰ і 60⁰

Чи правильно, що

Навколо кожної трапеції Навколо кожного прямокутника

можна описати коло? можна описати коло?

А	Б	В
так	ні	неможливо визначити

Три послідовні сторони описаного чотирикутника дорівнюють

2см; 3см; 4см 3см; 4см; 5см

Знайдіть четверту сторону.

А	Б	В	Г
2см	3см	4см	5см

6. Основи трапеції дорівнюють

5см і 7см 7см і 9см

Чому дорівнює довжина середньої лінії?

А	Б	В	Г
6см	7см	8см	9см

7. Вписаний кут становить

70⁰ 50⁰

Знайдіть величину відповідного центрального кута.

А	Б	В	Г
25⁰	100⁰	35⁰	140⁰

8. Знайти периметр трикутника, якщо його середні лінії дорівнюють:

4см; 5см; 6см 5см; 6см; 7см.

А	Б	В	Г
15см	30см	36см	18см

9. Встановити відповідність:

1. Описаний навколо кола чотирикутник

2. Вписаний у коло чотирикутник

3. Рівнобічна трапеція

4. Вписаний у коло кут

А. Сума протилежних кутів дорівнює 180⁰

Б. Бічні сторони рівні

В. Суми протилежних сторін рівні

Г. Дорівнює відповідному центральному куту

Д. Вимірюється половиною дуги кола, на яку він спирається

Учні обмінюються зошитами і за відповідями на слайді перевіряють тести свого сусіда (виставляють відповідні бали).

Підводимо ще раз підсумок уроку.

УІІ. Кросворд

1				8
				2
		3
			4
				5
	6
			7

Завдання:

1) Плоский кут із вершиною в центрі кола називається

(Центральним)

2) Чотирикутник називається … навколо кола, якщо всі його сторони дотикаються до цього кола

(Описаним)

3) Ім’я вченого, який довів теорему про паралельні прямі, які перетинають сторони кута

(Фалес)

4) Середня лінія трикутника паралельна одній з його сторін і дорівнює цієї сторони

(Половині)

5) Вписаний кут вимірюється половиною …., на яку він спирається

(Дуги)

6) Чотирикутник, у якого дві сторони паралельні, а дві інші не паралельні

(Трапеція)

7) Вписані кути що спираються на одну дугу, …

(Рівні)

8) Якщо ви все виконали, то ви...

(Молодці)

Всім дякую за урок!

Якщо залишається час, виконуємо додаткові задачі на слайдах (усно).

Урок 21

Тема Контрольна робота

Контрольна робота №2 8 кл.

Варіант 1

І рівень

Виберіть правильну відповідь.

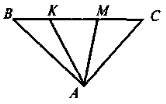
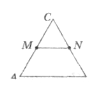
На рисунку АМ = МС, ВN = NС , АB = 6 см.

Довжина підрізка МN дорівнює:

а) 3 см; в) 5см;

б) 4 см; г) інша відповідь.

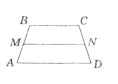
Відрізок МN у трапеції АВСD (ВС || АD)є середньою лінією

(див. рисунок). Якщо АD = 10 см, BС = 8 см, то МN дорівнює:

а) 18см; в) 9см;

б) 12см; г) інша відповідь.

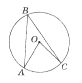
Градусна міра центрального кута AOC становить 80°

(див. рисунок). Чому дорівнює вписаний кут АВС?

а) 40°; в) 160°;

б) 80°; г) інша відповідь.

ІІ рівень

Виберіть правильну відповідь.

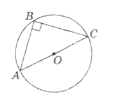
В коло радіуса 6 см, зображене на рисунку, вписано прямокутний

трикутник АВС ( = 90°) . Чому дорівнює гіпотенуза АС ?

а) 3 см; в) 12см;

б) 6см; г) інша відповідь.

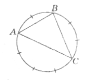На рисунку вершини трикутника АВС ділять коло у відношенні 2:3:4.

Знайдіть кути трикутника.

а) 80°; 20°; 80°; в) 40°; 60°; 80°;

б) 40°; 50°; 90°; г) 20°; 30°; 130° .

Діагональ прямокутника дорівнює 20 см. Знайдіть довжину відрізка, середини двох сусідніх сторін прямокутника.

а) 5 см; в) 20 см;

б) 15см; г) 10см.

ІІІ рівень

По один бік під прямої дано дві точки А і В на відстані 6 см і 14 см від неї. Знайдіть відстань від середини відрізка АВ до прямої.
Знайдіть середню лінію трапеції, описаної навколо кола, якщо її бічні сторони дорівнюють 5 см і 7 см.

IV рівень

Знайдіть кути рівнобедреного трикутника, бічна сторона якого стягує чверть дуги описаного кола.
Доведіть, що периметр описаної трапеції в чотири рази більший за середню лінію.

Контрольна робота №2 8 кл.

Варіант 2

І рівень

Виберіть правильну відповідь.

На рисунку МN — середня лінія трикутника АВС,

МN = 5 см. Довжина сторони АС дорівнює:

а) 6 см; в) 10см;

б) 8 см; г) інша відповідь.

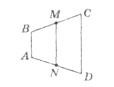
Відрізок МN — середня лінія трапеції АВСD (АB || CD) (див. рисунок).

Якщо АВ = 3 см, СD = 7 см, то довжина відрізка МN дорівнює:

а) 4см; в) 6 см;

б) 5 см; г) інша відповідь.

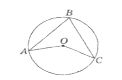
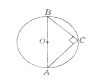
Градусна міра вписаного кута АВС становить 80°

(див. рисунок). Чому дорівнює центральний кут АОС?

а) 40°; в) 160°;

б) 80°; г) інша відповідь.

ІІ рівень

Виберіть правильну відповідь.

У коло, зображене на рисунку, вписано прямокутний трикутник

АВС (С = 90⁰) з гіпотенузою завдовжки 10 см. Чому дорівнює радіус кола:

а) 5 см; в) 20 см;

б) 10см; г) інша відповідь.

На рисунку вершини трикутника АВС ділять коло у відношенні 1:3:5.

Знайдіть кути трикутника АВС.

а) 10°; 80°; 100°; в) 10° ; 70° ; 100°;

б) 20°; 60°; 90°; г) 20°; 60°; 100° .

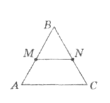
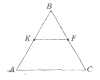Середня лінія КР розбиває рівносторонній трикутник АВС на чотирикутник

і трикутник (див. рисунок). Знайдіть периметр трикутника КВF,

якщо АВ = 10 см.

а) 5см; в) 15см;

б) 10см; г) 20см.

ІІІ рівень

Кінці діаметра віддалені під дотичної до кола па 5 см і 15 см. Знайдіть радіус кола.
Знайдіть периметр трапеції, описаної навколо кола, якщо її бічні сторони дорівнюють 9 см і 10 см.

IV рівень

Знайдіть кути рівнобедреного трикутника, бічна сторона якого стягує шосту частину дуги описаного кола.
Доведіть, що середня лінія описаної рівнобедреної трапеції дорівнює бічній стороні.

docx

Завантажити

Зберегти на потім

Додав(-ла)

Котис Оксана Володимирівна

Пов’язані теми

Геометрія, 8 клас, Розробки уроків

Додано

24 жовтня 2018

Переглядів

5387

Оцінка розробки

Відгуки відсутні