Контрольна робота "Квадратна нерівність. Системи рівнянь другого степеня з двома змінними"
09 лютого
Контрольна робота з алгебри № 3
«Квадратна нерівність. Системи рівнянь другого степеня з двома змінними»
І варіант
1.Яка з нерівностей не є квадратною?
А) х2 + 2х > х2 + 1; Б) х2 + 3х >2; В) х2 + 4х > 2х2; Г) х2 + 4х + х2 >0.
2.Яке з чисел належить множині розв’язків нерівності х2 + 6х + 8 ≥ 0?
А) -3![]() ; Б) -2,5; В) -2; Г) -3,99.
; Б) -2,5; В) -2; Г) -3,99.
3.Розв'яжіть нерівність х2 + 5х – 6 < 0.
А) ( -6; 1); Б) ( - ∞; -6 ) U (1; + ∞); В) ( -1; 6); Г) ( - ∞; -1) U (6; + ∞).
4.Знайдіть область визначення функції f(х) = ![]()
А) ( -3; 12); Б) ( -12; 3); В) ( - ∞; - 3) U (12; + ∞); Г) ( - ∞; -12) U (3; +∞).
5. Розв’яжіть систему ![]()
А) (4;3); Б) (3;4); В) (4;3), (3;4); Г) (-4; -3).
6.За допомогою якої з наведених систем рівнянь можна знайти катет прямокутного трикутника, якщо відомо, що один із катетів більший за другий на 7см, а гіпотенуза дорівнює 13см.
А) ![]() ; Б) )
; Б) ) ![]() ; В)
; В) ![]() ; Г) )
; Г) ) ![]() .
.
7. Встановіть відповідність між нерівностями та їх розв’язками.
1) х2 – 25 < 0 А) (- ∞; + ∞)
2) 5х – х2 > 0 Б) (-5;5)
3) х2 – 10х + 25 < 0 В) - 5
4) х2 + 10х + 25 ≤ 0 Г) ( 0; 5)
Д) розв'язків немає.
8.Знайдіть область визначення функції у = ![]() +
+ ![]() .
.
9.Розв’яжіть задачу. Із міста А до міста В виїхала вантажівка. А через 20 хв за нею виїхав легковик, швидкість якого на 40 км/год більша. Знайдіть швидкості автомобілів, якщо вантажівка прибула до міста В на 25 хв пізніше, а відстань між містами 180км.
Додаткове завдання. Розв'яжіть систему рівнянь 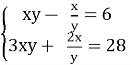


про публікацію авторської розробки
Додати розробку
