Презентація "Взаємне розміщення прямих у просторі"

паралельнімимобіжніперетинаються. Розташування прямих у просторіstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Мета уроку: сформувати поняття паралельних мимобіжних прямих та прямих, що перетинаються, вивчити ознаки паралельності прямих; виробити навички застосування вивченого матеріалу до розв'язування задач.style.colorfillcolorfill.type

Сьогодні на уроці ми такожрозвиваємо просторову уяву, логічне мислення, спостережливість, уміння чітко й правильно висловлювати думку; виховуємо культури математичних записів та мови.style.colorfillcolorfill.type

Афоризм Рене Декарта представляє девіз уроку: Мало мати хороший розум, головне – добре його застосовувати.style.colorfillcolorfill.typestyle.colorfillcolorfill.type

Основні поняття стереометріїТочка(А)АПряма(АВ або а)АВа. Площина(α)αАВПряма АВ АВВідрізок АВ АВПромінь АВ А

Поняття та зображення площини. Площину зображають так:αабо так:β

αЗверніть увагу!!!Площина, так само як і пряма, є нескінченною:

Площину можна провести: Через будь-які 3 точки, що не лежать на одній прямій:αАВС2) Через пряму і точку, що не лежить на нійαАВС3) Через дві прямі, що перетинаютьсяαАВСЦю площину α можна позначати так: (АВС)

Властивість паралельних прямих на площині: Через точку, що не лежить на прямій, можна провести пряму, яка паралельна даній, і тільки одну.αa. АВзаємне розташування двох прямих на площиніααЯкщо дві прямі лежать у площині, то вони між собою:або перетинаються,або паралельні (a||b)ababb

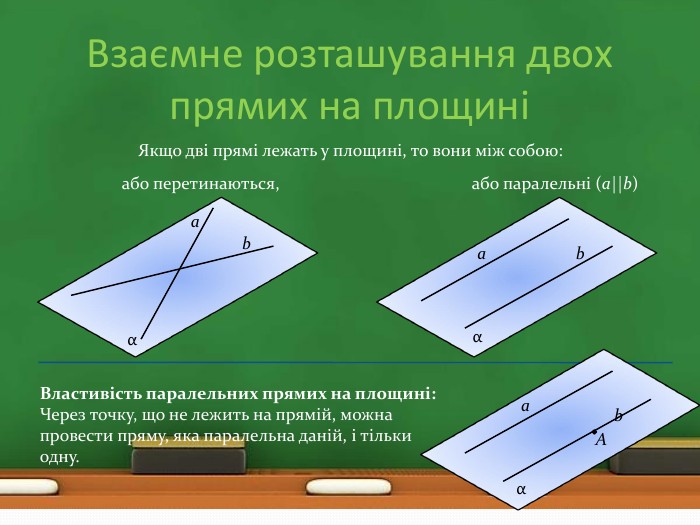
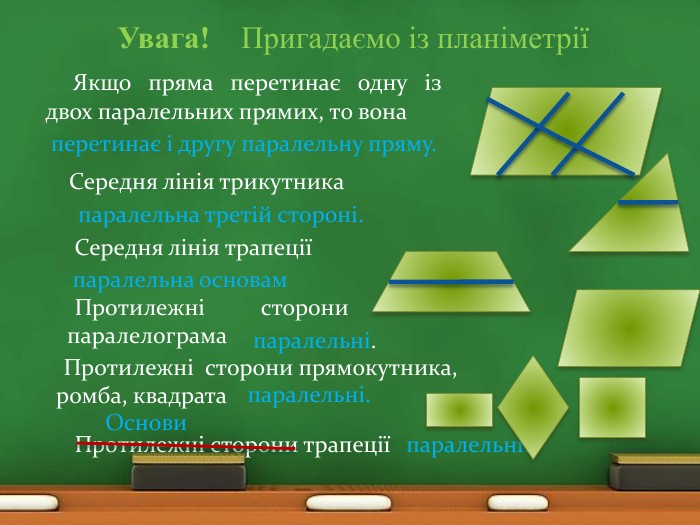
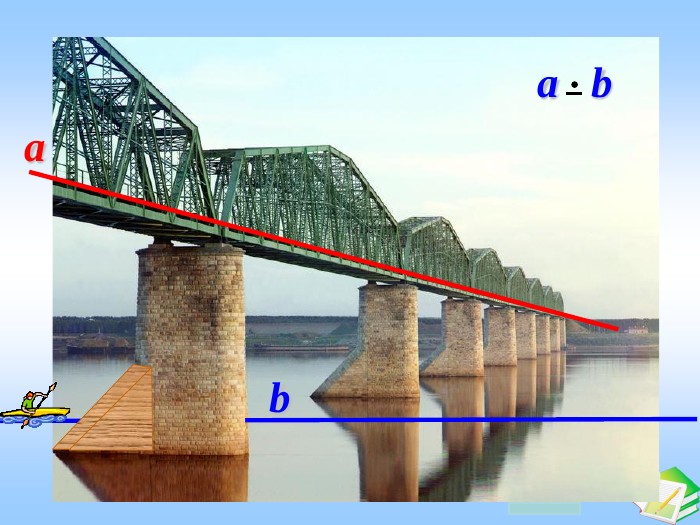
Увага! Пригадаємо із планіметріїЯкщо пряма перетинає одну із двох паралельних прямих, то вона перетинає і другу паралельну пряму. Середня лінія трикутникапаралельна основампаралельна третій стороні. Середня лінія трапеції Протилежні сторони паралелограма паралельні. Протилежні сторони прямокутника, ромба, квадрата. Протилежні сторони трапеції паралельні.паралельні. Основи

Означення паралельних прямих ab. Дві прямі, що лежать в одній площині й не перетинаються називають паралельними. Означення мимобіжних прямих. Дві прямі, що не лежать в одній площині називають мимобіжними. Мabstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

перетинаютьсямимобіжніДві прямі у просторіЛежать в одній площиніНе лежать в одній площиніВзаємне розміщення прямих у просторі паралельніМababab а b а b

IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIi. Наочне уявлення мимобіжних прямих дають дві дороги, одна з яких проходить по мосту, а інша під мостом.

aba b

Знайдіть на малюнку дві паралельні прямі. Знайдіть мимобіжні прямі.

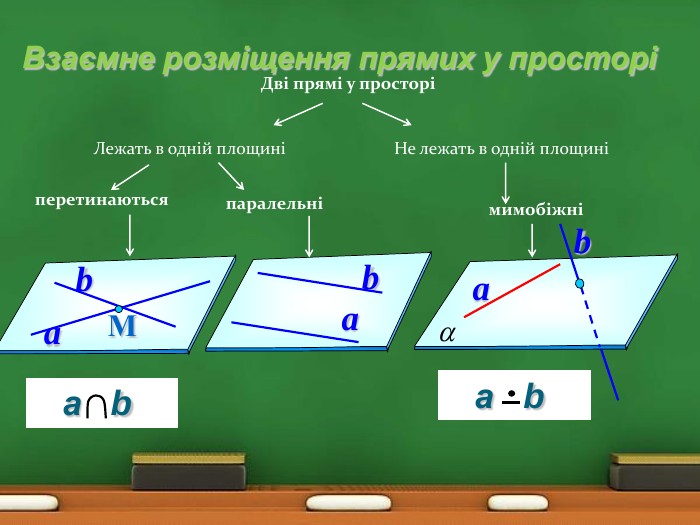
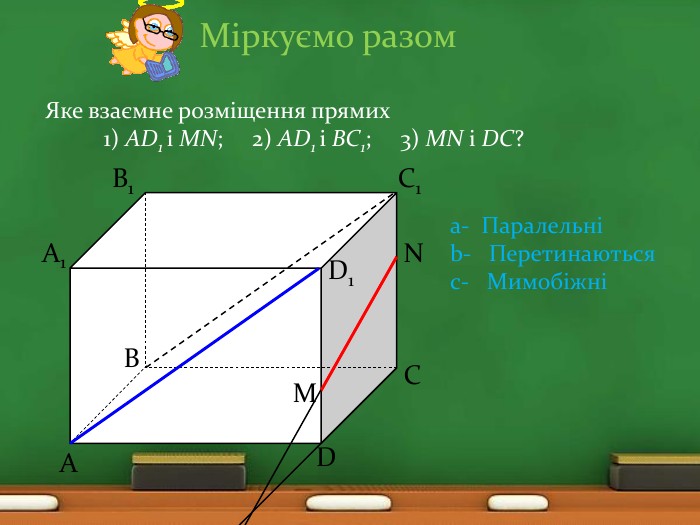
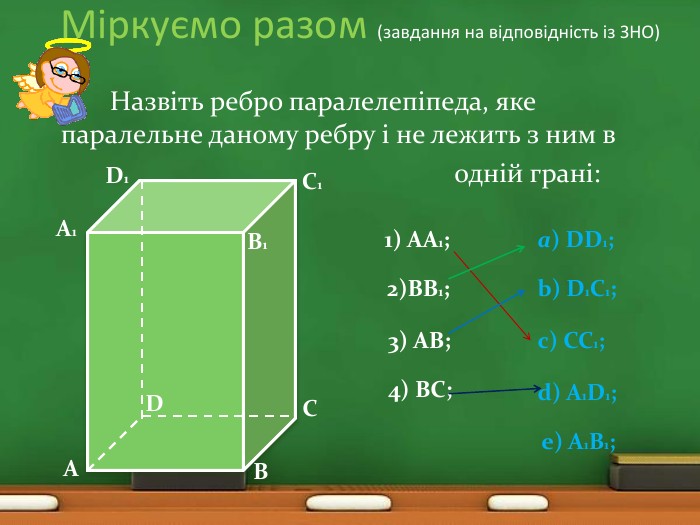
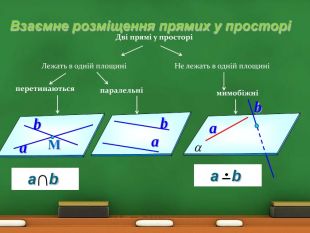
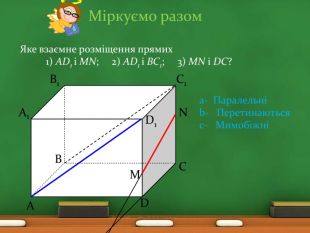
Міркуємо разом. Чи правильно, що:дві прямі, що не є паралельними, мають спільну точку;дві прямі, що не є мимобіжними, лежать в одній площині; дві прямі, що лежать в одній площині, паралельні;дві паралельні прямі лежать в одній площині? Не завжди. Так. Не завжди. Такa - Такb - Ніc - Не завжди

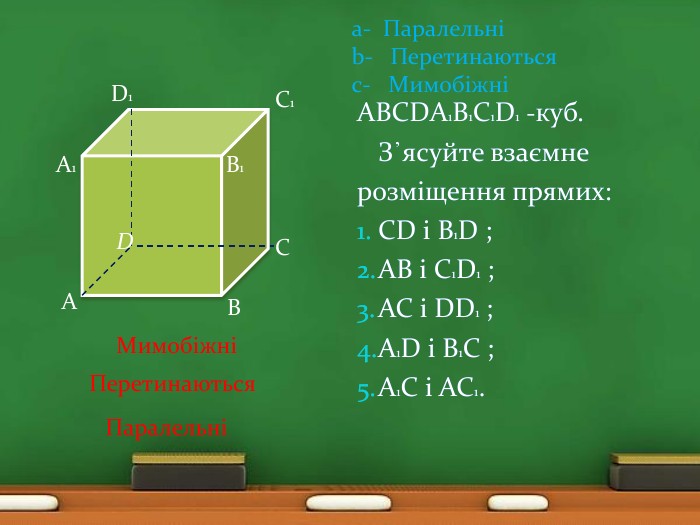
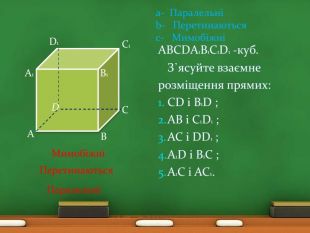
АВСDА1 В1 С1 D1 -куб. З᾽ясуйте взаємнерозміщення прямих: СD і В1 D ;АВ і С1 D1 ;АС і DD1 ;А1 D і В1 С ;А1 С і АС1. ВВ1 А1 С1 СDАD1 МимобіжніПеретинаються. ПаралельніАВСDА1 В1 С1 D1 -куб. З᾽ясуйте взаємнерозміщення прямих: СD і В1 D ;АВ і С1 D1 ;АС і DD1 ;А1 D і В1 С ;А1 С і АС1.a- Паралельніb- Перетинаютьсяc- Мимобіжніrr

Властивості паралельних прямих 2. Усі паралельні прямі, що перетинають задану пряму, лежать з нею в одній площині. Через точку простору, що не лежить на прямій, можна провести пряму, паралельну даній,i тільки одну.аb. Adcabα

Увага! АА1‖ВВ1‖СС1. Чи належать ці прямі одній площині? Як треба змінити рисунок, якщо додати до умов задачі існування прямої l, яка перетинає всі задані прямі? AA1 В1 С1 СВНі

АDСВB1 С1 D1 А1 Яке взаємне розміщення прямих 1) AD1 і МN; 2) AD1 і ВС1; 3) МN і DC?NM Міркуємо разомa- Паралельніb- Перетинаютьсяc- Мимобіжні

Назвіть ребро паралелепіпеда, яке паралельне даному ребру і не лежить з ним в одній грані: А13) АB;4) BC;B1 DАВС1) AA1;2)BB1;D1 C1c) CC1;b) D1 C1;a) DD1;d) А1 D1;e) А1 B1;Міркуємо разом (завдання на відповідність із ЗНО)ppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xrrrr

Міркуємо разом Скільки ребер куба АВСDА1 В1 С1 D1 проходить через дану його вершину паралельно заданому ребру: 1) А і В1 С1; 2) D і ВВ1; 3) С1 і АА1. Відповідь обгрунтуйте. А1 B1 ВСDD1 C1 А1a- 1b- 2c- 3ppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xrppt_xppt_x

Задача (розв’язуємо біля дошки) Яким прямим паралельні сторони перерізу прямокутного паралелепіпеда АВСDА1 В1 С1 D1 , якщо його перерізом є прямокутник із сторонами: 1) AB i AD1; 2) B1 C1 i C1 D; 3) BD i BB1. АВD1 А1 DСС1 В1

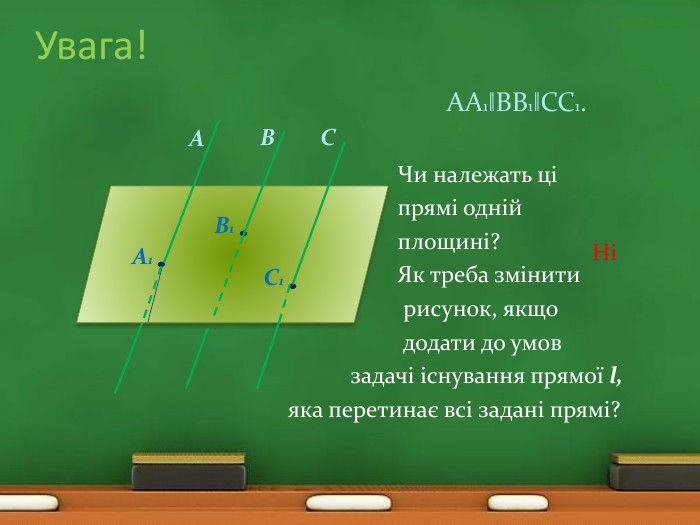
Задача (розв’язуємо самостійно в зошитах)Доведіть, що всі прямі, які перетинають кожну із двох паралельних прямих, лежать в одній площині. План доведення1. Оскільки прямі a і b паралельні, то вони визначають … 2. Нехай с – довільна пряма, що перетинає пряму а у точці А, а пряму b у точці В. Точки А і В лежать у площині…3. Оскільки дві точки прямої с лежать у площині … , то й пряма с … 4. Таким чином, усі прямі, які … дві дані паралельні прямі …

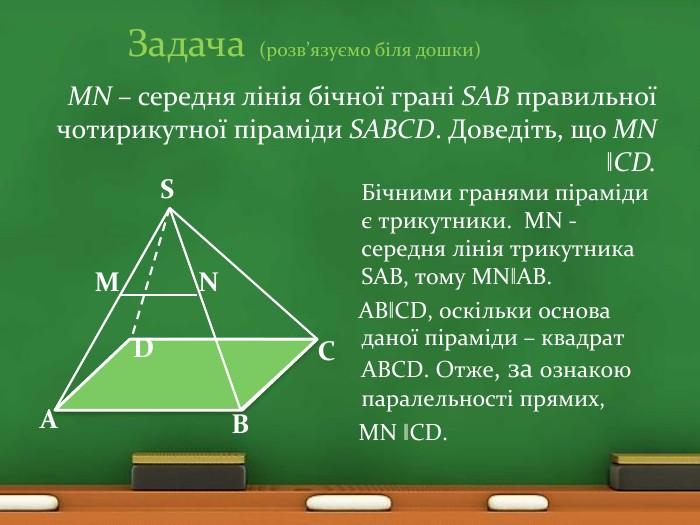
МN – середня лінія бічної грані SAB правильної чотирикутної піраміди SABCD. Доведіть, що MN ‖CD. CDNMSВА Бічними гранями піраміди є трикутники. МN - середня лінія трикутника SАВ, тому МN‖АВ. АВ‖СD, оскільки основа даної піраміди – квадрат АВСD. Отже, за ознакою паралельності прямих, МN ‖СD. Задача (розв’язуємо біля дошки)ppt_xppt_xppt_xppt_xppt_xppt_xppt_x

Виконання вправ. Задача. Прямі AB і CD паралельні. Чи можуть бути мимобіжними прямі AC і BD? А чи можуть вони перетинатись?Розв’язання. Якщо AB||CD, то прямі AB і CD лежать в одній площині, значить, і точки A, B, C, D лежать в одній площині. Отже, прямі AC і BD також лежать в одній площині, а значить, можуть перетинатися, але не можуть бути мимобіжними. Задача. Прямі AB і CD мимобіжні. Чи можуть бути паралельними прямі AC і BD? А чи можуть вони перетинатись?Розв’язання. Якщо б могло бути, що AC||BD або AC перетинала BD,то точки A, B, C, D лежали б в одній площині,а цього бути не може, тому що суперечить умові задачі. Отже, прямі AC і BD не можуть бути ні паралельними, ні перетинатись.

Перевіримо свої знання1. Площини α і β перетинаються. Отже, прямі а і в, зображені на малюнку a - мимобіжні; b – перетинаються; c - паралельні; d - можуть бути розміщені по-різному залежно від розміщення площин. ваβαppt_xppt_xppt_x

2. Два прямокутники АВСD і АEFD лежать у різних площинах. Прямі ВС і EF … a - мимобіжні; b – перетинаються; c – паралельні; d - можуть бути розміщені по-різному залежно від розміщення площин.3. Діагоналі протилежних граней АА1 В1 В і DD1 С1 С куба АВСDА1 В1 С1 D1 … a - мимобіжні; b – паралельні; c – паралельні чи мимобіжні; d - перетинаються.

Порахуємо бали !style.colorfillcolorfill.type

Домашнє завдання. Прочитати § 6 (розділ 3)Розв’язати №219, №221 Для найкмітливіших: +№225 Для допитливих: опрацювати матеріал на ст.68-69

Рефлексія

Багато чого з математики не залишається в пам'яті, але коли зрозумієш її, тоді легко при нагоді згадати призабуте. М. В. Остроградський. Дякую за увагу!ppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_x