Контрольна робота з геометрії на тему "Паралельність площин у просторі" 10 клас

Паралельність площин

Контрольна робота

1 варіант

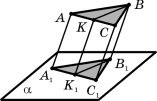
1. ABCDA₁B₁C₁D₁- куб. Точки M,N,K – середини ребер A₁B₁ , A₁D₁ ,AA₁ відповідно. Обґрунтуйте взаємне розміщення площин MNK та B₁D₁A.

Б. Якщо BK — висота трикутника ABС, то B₁K₁ обов’язково висота трикутника A₁B₁С₁.

В. Якщо BK — медіана трикутника ABС, то B₁K₁ обов’язково медіана трикутника A₁B₁С₁.

3. Через точку К, яка не лежить між паралельними площинами α і β, проведено прямі, які перетинають площину α в точках А і В, а площину β в точках А₁ і В₁ відповідно. Знайдіть АВ і А₁В₁, якщо АК : АА₁= 1: 17, АВ+А₁В₁=57см.

4. Паралелограм  A₁B₁C₁D₁ – проекція ромба ABCD. Точка К – середина АВ. Побудувати проекцію перпендикуляра, проведеного з точки К до діагоналі АС.

Паралельність площин

Контрольна робота

2 варіант

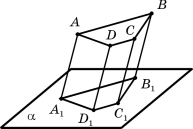
1. ABCDA₁B₁C₁D₁- куб. Точки M,N,S – середини ребер A₁D₁ , C₁D₁ ,DD₁ відповідно. Обґрунтуйте взаємне розміщення площин MNS та A₁DC₁.

Г. Якщо AB = 2CD, то відрізки A₁B₁ і C₁D₁ можуть бути рівними.

3. Площини  α і β паралельні. Через точку М , що знаходиться між цими площинами, проведено дві прямі. Одна з них перетинає площини α і β у точках А₁ і В₁ , а друга – у точках А₂ і В₂ відповідно. Знайдіть довжини відрізків А₂М і МВ₂, якщо А₁М : А₁В₁= 2 :5, А₂В₂=35см.

4. Трикутник A₁B₁C₁ є зображенням у паралельній проекції рівностороннього трикутника АВС. Побудувати зображення перпендикулярів, які проведено із середини сторони АВ на сторони ВС і АС.