Контрольна робота з геометрії "Паралельність прямих і площин у просторі"

Відповіді

1 варіант

І рівень

1 а

2 в

3 в

4 б

5 в

ІІ рівень

За умовою відрізок АВ перетинають прямі АА₁, ВВ₁ і ММ₁ (М є АВ), причому (М є АВ) (див. мал.). Отже, відрізок АВ і прямі АА₁, ВВ₁, ММ₁ лежать в одній площині β , відмінний від площини α, оскільки відрізок АВ не лежить у площини α.

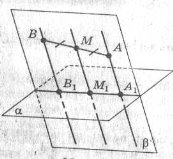
   За умовою прямі АА₁, ВВ₁ і ММ₁ перетинають площину  α у точках А₁, В₁ і М₁, тобто площини α і β мають спільні точки. За аксіомою С₂ ці точки належать спільні прямій А₁В₁. Отже, М₁ є А₁В₁.

За теоремою Фалеса з умов АМ = МВ і АА₁ ║ВВ₁ ║ММ₁ випливає, що А₁М₁ = В₁М₁. Звідси ММ₁ – середня лінія трапеції АВВ₁А₁ (якщо відрізок АВ не паралельний площини α).  За властивістю середньої лінії трапеції          ММ₁=0,5·(АА₁ + ВВ₁).

Виконаємо обчислення:

ММ₁ = 0,5·(5+7)=6 (м).

Відповідь: 6м.

ІІІ рівень

За умовою паралелограм АВСD  не перетинається площиною α             (див. мал.).  Через вершини паралелограма проведено паралельні прямі              (AА₁ ║ВВ₁ ║ СС₁ ║DD₁), які  перетинають площину α в точках А₁, В₁, С₁ і D₁ відповідно. Знайдемо DD₁.  Розв’яжемо задачу в загальному вигляді: АА₁ = а, ВВ₁ = b, CC₁ = c.

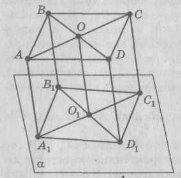
   У паралелограмі АВСD проведемо діагоналі АС і ВD, які перетинаються у точці О і діляться цією точкою навпіл. Через  точку О проведемо пряму, паралельну прямій СС₁,  так, що вона перетинає площину α  у  точці О₁ (якщо площина перетинаю одну  з паралельних прямих, то вона перетинає і другу пряму).

За умовою АА₁ ║СС₁, за побудовою ОО₁║СС₁, тоді за ознакою паралельності  прямих маємо, що АА₁║ОО₁ . Таким чином, відрізок АС перетинають паралельні прямі  (АА₁ ║ОО₁ ║СС₁), отже, вони лежать у одній площині β, відмінній від площини α. Площини α і β мають спільні точки (А₁, О₁ і С₁), за аксіомою С₂ вони перетинаються по прямій, що проходить через ці точки. Таким чином, О₁ є А₁С₁.

 а) Якщо АА₁≠СС₁, то А₁АСС₁ – трапеція (площина α не перетинає паралелограм ABCD).

 За теоремою Фалеса точка О₁ – середина відрізка А₁С₁, тоді ОО₁ –середня лінія трапеції А₁АСС₁, тобто

                         ОО₁ = 0,5·(АА₁ + СС₁) = 0,5·(а+с)     (1)

 Аналогічно доводиться, що коли ВВ₁≠DD₁, то ОО₁ – середня лінія трапеції ВВ₁ D₁D, тобто

                         ОО₁ = 0,5·(ВВ₁ +DD₁)                        (2)

Із співвідношень (1) і (2) отримуємо:

АА₁+СС₁=ВВ₁ + DD₁.

Звідси  DD₁ = AA₁ + CC₁ – BB₁,          тобто  DD₁ = a + c-b                 (3)

б) Якщо АА₁=СС₁ (а=с), то АА₁С₁С – паралелограм і ОО₁=АА₁=СС₁.

Якщо  В₁ВDD₁ – паралелограм, то формула (3) дає вірний результат, тобто DD₁=AA₁=BB₁=OO₁=CC₁.

Використовуючи формулу (3), отримуємо:

DD₁ = 2+8-3=7 (м).  

Відповідь: 7м.

2 варіант

І рівень

1 а

2 г

3 в

4 г

5 в

ІІ рівень

За умовою відрізок АВ перетинають прямі АА₁, ВВ₁ і ММ₁ (М є АВ), причому (М є АВ) (див. мал.). Отже, відрізок АВ і прямі АА₁, ВВ₁, ММ₁ лежать в одній площині β , відмінний від площини α, оскільки відрізок АВ не лежить у площини α.

   За умовою прямі АА₁, ВВ₁ і ММ₁ перетинають площину  α у точках А₁, В₁ і М₁, тобто площини α і β мають спільні точки. За аксіомою С₂ ці точки належать спільні прямій А₁В₁. Отже, М₁ є А₁В₁.

За теоремою Фалеса з умов АМ = МВ і АА₁ ║ВВ₁ ║ММ₁ випливає, що А₁М₁ = В₁М₁. Звідси ММ₁ – середня лінія трапеції АВВ₁А₁ (якщо відрізок АВ не паралельний площини α).  За властивістю середньої лінії трапеції          ММ₁=0,5·(АА₁ + ВВ₁).

Виконаємо обчислення:

ММ₁ = 0,5·(3,6+4,8)=4,2 (м).

Відповідь: 4,2м.

ІІІ рівень

За умовою паралелограм АВСD  не перетинається площиною α             (див. мал.).  Через вершини паралелограма проведено паралельні прямі              (AА₁ ║ВВ₁ ║ СС₁ ║DD₁), які  перетинають площину α в точках А₁, В₁, С₁ і D₁ відповідно. Знайдемо DD₁.  Розв’яжемо задачу в загальному вигляді: АА₁ = а, ВВ₁ = b, CC₁ = c.

   У паралелограмі АВСD проведемо діагоналі АС і ВD, які перетинаються у точці О і діляться цією точкою навпіл. Через  точку О проведемо пряму, паралельну прямій СС₁,  так, що вона перетинає площину α  у  точці О₁ (якщо площина перетинаю одну  з паралельних прямих, то вона перетинає і другу пряму).

За умовою АА₁ ║СС₁, за побудовою ОО₁║СС₁, тоді за ознакою паралельності  прямих маємо, що АА₁║ОО₁ . Таким чином, відрізок АС перетинають паралельні прямі  (АА₁ ║ОО₁ ║СС₁), отже, вони лежать у одній площині β, відмінній від площини α. Площини α і β мають спільні точки (А₁, О₁ і С₁), за аксіомою С₂ вони перетинаються по прямій, що проходить через ці точки. Таким чином, О₁ є А₁С₁.

 а) Якщо АА₁≠СС₁, то А₁АСС₁ – трапеція (площина α не перетинає паралелограм ABCD).

 За теоремою Фалеса точка О₁ – середина відрізка А₁С₁, тоді ОО₁ –середня лінія трапеції А₁АСС₁, тобто

                         ОО₁ = 0,5·(АА₁ + СС₁) = 0,5·(а+с)     (1)

 Аналогічно доводиться, що коли ВВ₁≠DD₁, то ОО₁ – середня лінія трапеції ВВ₁ D₁D, тобто

                         ОО₁ = 0,5·(ВВ₁ +DD₁)                        (2)

Із співвідношень (1) і (2) отримуємо:

АА₁+СС₁=ВВ₁ + DD₁.

Звідси  DD₁ = AA₁ + CC₁ – BB₁,          тобто  DD₁ = a + c-b                 (3)

б) Якщо АА₁=СС₁ (а=с), то АА₁С₁С – паралелограм і ОО₁=АА₁=СС₁.

Якщо  В₁ВDD₁ – паралелограм, то формула (3) дає вірний результат, тобто DD₁=AA₁=BB₁=OO₁=CC₁.

Використовуючи формулу (3), отримуємо:

DD₁ = 4+1-3=2 (м).  

Відповідь: 2м.