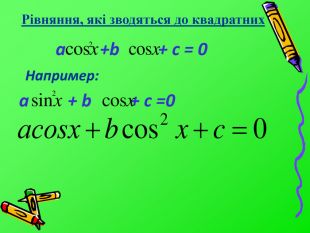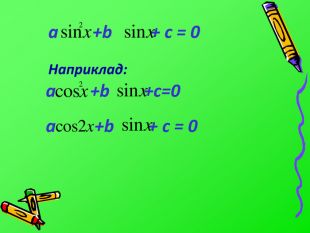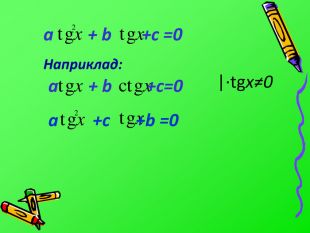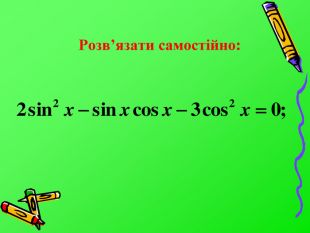Презентація ,,Способи розв'язання тригонометричних рівнянь"










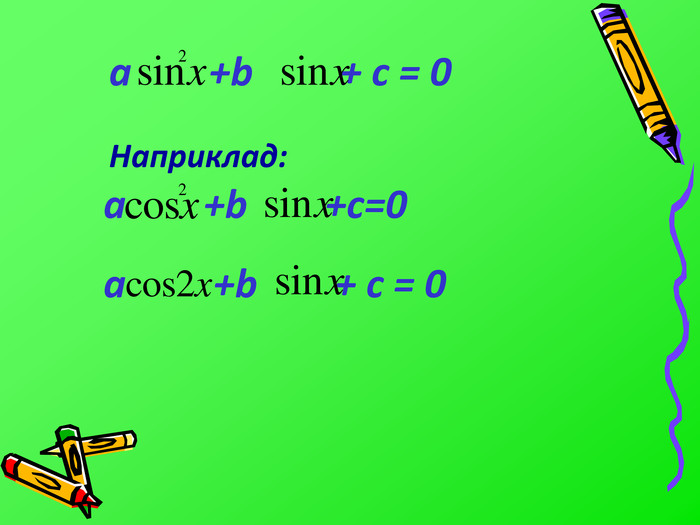
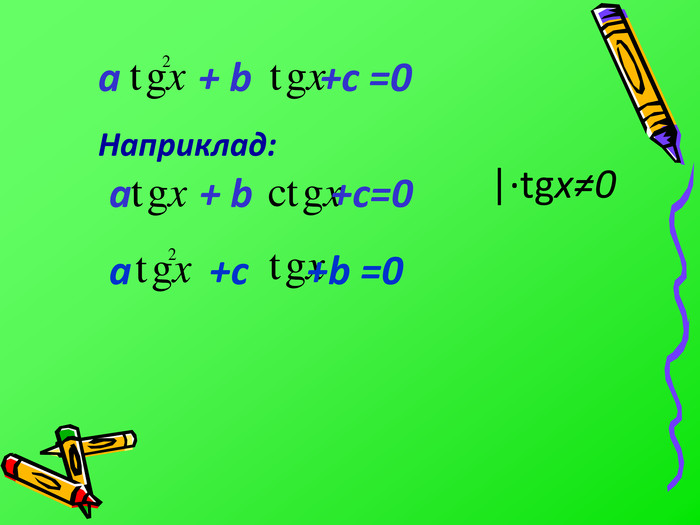
![Розв’язок: sinx =t |t|≤ 1, т.к. E(sinx)=[-1;1] at² +bt + c =0 cosx =t |t|≤1, т.к. E(cosx)=[-1;1]tgx =tt R,т.к. E(tgx)=R Розв’язок: sinx =t |t|≤ 1, т.к. E(sinx)=[-1;1] at² +bt + c =0 cosx =t |t|≤1, т.к. E(cosx)=[-1;1]tgx =tt R,т.к. E(tgx)=R](/uploads/files/1287709/219014/234942_images/17.jpg)












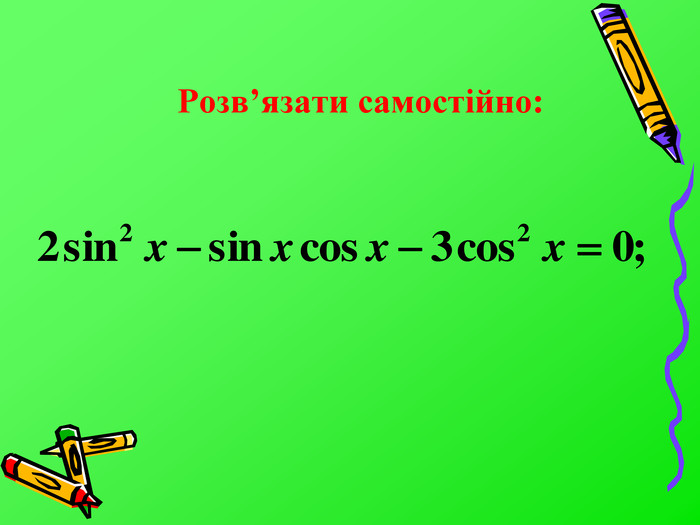

























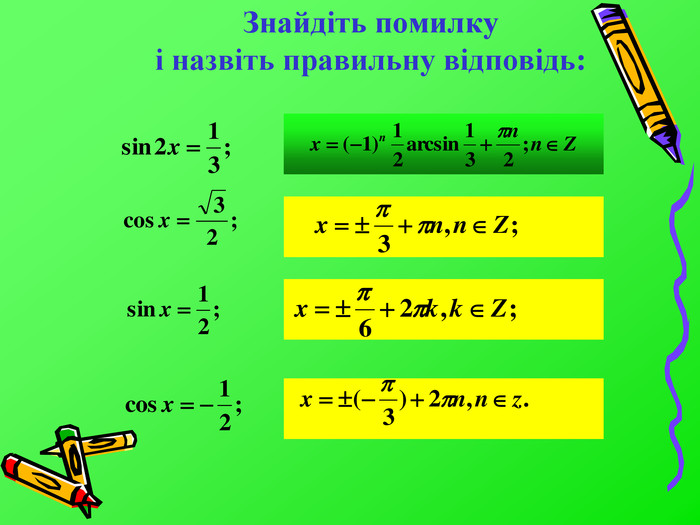
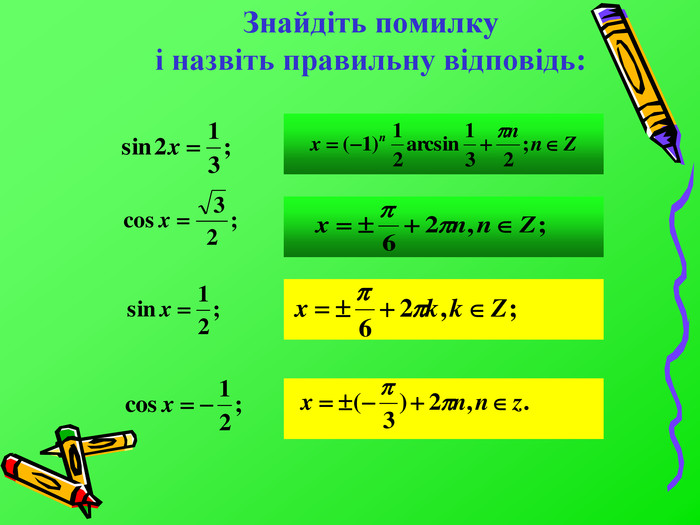
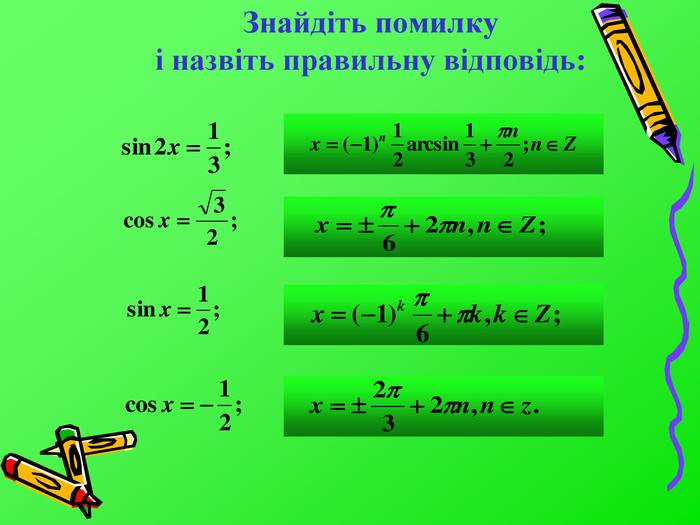
На даний момент ми знаємо, що: Якщо |a|≤1, то рішення рівняння cosx=a має вигляд x=±arccosa+2πn, nєZ;Якщо |a|≤1, то рішення рівняння sinx=a має вигляд x=(-1)n arcsina+πn, nєZ;або, що те ж саме, x1=arcsina+2πk, kєZ x2=π-arcsina+2пk, kєZ;Якщо |a|>1, то рівняння cosx=a, sinx=a не мають рішення;Рішення рівняння tgx=a для любого значення a мають вигляд x=arctga+πn, nєZ.
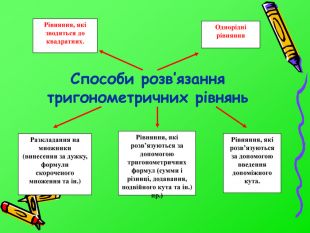
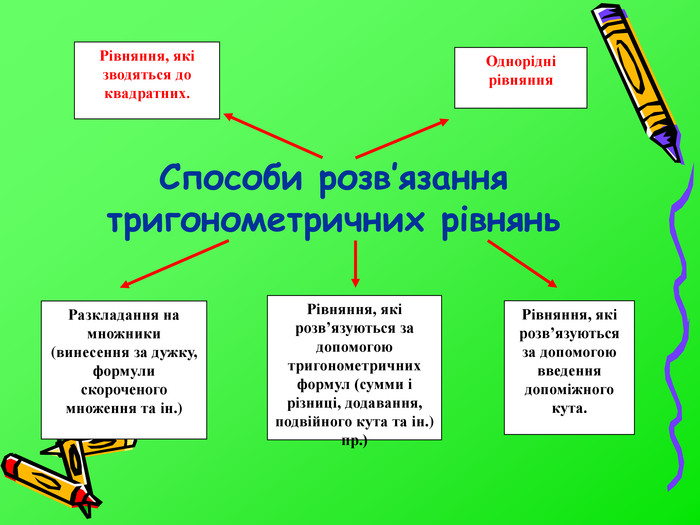
Способи розв’язання тригонометричних рівнянь. Разкладання на множники (винесення за дужку, формули скороченого множення та ін.)Рівняння, які зводяться до квадратних. Однорідні рівняння. Рівняння, які розв’язуються за допомогою введення допоміжного кута. Рівняння, які розв’язуються за допомогою тригонометричних формул (сумми і різниці, додавання, подвійного кута та ін.) пр.)
Алгоритм рішення однорідних тригонометричних рівнянь другого степеня. Подивитись, чи є в рівнянні член asin2x;Якщо цей член міститься, тобто а≠0, то рівняння розв’язується діленям обох його частин на cos2x і подальшим введенням нової змінної z=tgx;Якщо цей член не міститься, тобто а=0, то рівняння розв’язується методом розкладання на множники: за дужки виносять cosx;


про публікацію авторської розробки
Додати розробку