Контрольна робота з теми: "Функція"

Варіант І

1. На якому з рисунків схематично зображено графік непарної функції? (0,5 б)

2. Область визначення функції y = x³  є ...

а) ( -∞; 0 ) U ( 0; +∞ ),   б) [ 0; +∞ ) , в) ( -∞; +∞ ),   г) ( -∞; 0 )     (0,5 б)                        

3. Відомо, що функція y = f( x ) – непарна і f( 3 ) = 4.    (0,5 б)

Знайти f ( -3 ). а)  -4;    б) 4;    в) –3;    г) 3 

4. Знайти область визначення функції y = +.    (1 б)

5. Дослідити на парність функцію f( x ) = 8x³ – x⁵.      (0,5 б)

6. Обчисліть: а) б)     (1 б)

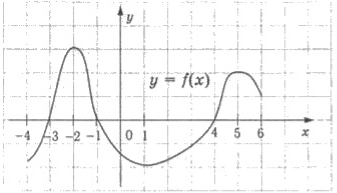
7. Для функції, графік якої зображено на рисунку,                   (2 б)

а) знайти значення аргументу, при яких значення функції дорівнює нулю;

б) вказати проміжки, на яких функція набуває додатних значень.  

8. Знайдіть область визначення функції: у =   (1 б)
9. Обчислити:  .     (0,5 б)
10. Знайдіть вираз, що дорівнює виразу 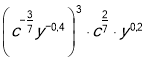 (0,5 б)
11. Обчисліть значення виразів,встановіть відповідність: 

1)     А)       (2 б)

2)                               Б)  27

3)                                В)  8

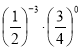4)                              Г) 

  Д)  4

12. Спростіть вираз 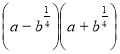. (1 б)  

13.  Обчислити: 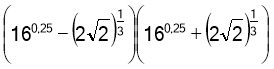   (1 б)

Варіант ІІ

1. На якому з рисунків схематично зображено графік парної функції? (0,5 б)

2. Область визначення функції y =  є ...     (0,5 б)

а) ( -∞; 0 ) U ( 0; +∞ )     б) [ 2; +∞ ) в) ( -∞; +∞ )   г) ( -∞; 0 )       

3. Відомо, що функція y = f( x ) – парна і f( 2 ) = 3.

Знайти f ( -2 ).  а) –3;    б) 3;    в) -2;    г) 2.  (0,5 б)        

4. Знайти область визначення функції y = +.               (1 б)

5. Дослідити на парність функцію f( x ) = 7x⁴ – x².                 (0,5 б)

6. Обчисліть: а)    б)           (1 б)

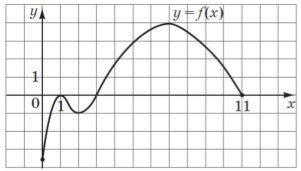
7. Для функції, графік якої зображено на рисунку,    (2б)

а) знайти значення аргументу, при яких значення функції дорівнює нулю;

б) вказати проміжки, на яких функція спадає.     

8. Знайдіть область визначення функції: у =     (1 б)

9. Обчислити:       (0,5 б)

10. Винесіть множник із-під знака радикала .(0,5)

11. Обчисліть значення виразів і встановіть відповідність:

1)     А)     (2б)

2)                              Б)  8

3)                               В)  2

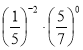4)                              Г)  25

  Д)

12. Спростіть вираз 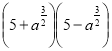.   (1 б)

13.  Обчислити: 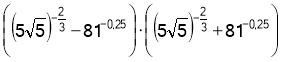            (1 б)

Варіант ІІІ

1. На якому з рисунків схематично зображено графік непарної функції? (0,5 б)

2. Область визначення функції y =  є ... (0,5 б)

а) ( -∞; 0 ) U ( 0; +∞ )     б) [ 0; +∞ ) в) ( -∞; +∞ )      г) ( -∞; 0 )      

3. Відомо, що функція y = f( x ) – непарна і f( -4 ) = 6.

Знайти f ( 4 ). а)  -4; б) 4; в) –6; г) 6 .    (0,5 б)

 4. Знайти область визначення функції y = +.              (1 б)

5. Дослідити на парність функцію f( x ) = 5 x⁴-2 .             (0,5 б)    

6. Обчисліть:  а)      б)                       (1 б)            

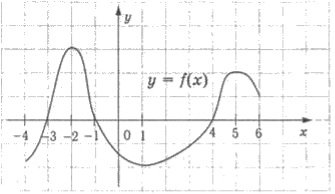
7. Для функції, графік якої зображено на рисунку,    (2б)

а) знайти значення аргументу, при яких значення функції дорівнює нулю;

б) вказати проміжки, на яких функція набуває додатних значень.   

8. Знайдіть область визначення функції у = (1 б)
9. Обчислити: (0,5 б)
10. Знайдіть вираз, що дорівнює виразу . (0,5 б)
11. Обчисліть значення виразів і встановіть відповідність:

1)     А)           (2б)

2)                               Б)  27

3)                               В)  8

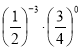4)                              Г) 

                             Д)  4

12. Спростіть вираз 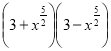.  (1 б) 

13.  Обчислити: 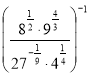        (1 б)

Варіант ІV

1. На якому з рисунків схематично зображено графік парної функції? (0,5 б)

2. Область визначення функції y = 2-x  є ... (0,5 б)

а) ( -∞; 0 ) U ( 0; +∞ )     б) [ 2; +∞ ) в) ( -∞; +∞ )    г) ( -∞; 0 )   (0,5 б)

3. Відомо, що функція y = f( x ) –парна і f( -2 ) = -3.

Знайти f ( 2 ).  а) –3;    б) 3;    в) -2;    г) 2.(0,5б)         

4. Знайти область визначення функції y = +.            (1 б)

5. Дослідити на парність функцію f( x ) = 3x⁷+4 .                 (0,5б)

6. Обчисліть: а)      б)          (1 б)      

7. Для функції, графік якої зображено на рисунку,    (2б)

а) знайти значення аргументу, при яких значення функції дорівнює нулю;

б) вказати проміжки, на яких функція набуває від’ємних значень.     

8. Знайдіть область визначення функції  у =  (1 б)
9. Обчислити:     (0,5 б)
10. Винесіть множник із-під знака радикала .(0,5 б)
11. Обчисліть значення виразів і встановіть відповідність:

1)     А)              (2б)

2)                              Б)  8

3)                               В)  2

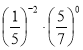4)                              Г)  25

                             Д)

12. Спростіть вираз 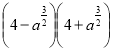.(1 б)

13. Обчислити: 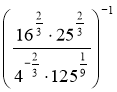    (1 б)