Контрольні роботи з алгебри та початків аналізу для 10 класу. Профільний рівень
Контрольні роботи з алгебри і початків аналізу для 10 класу . Профільний рівень.
Канарська Людмила Василівна, вчитель математики Черкаської гімназії № 9 ім. О. М. Луценка Черкаської міської ради Черкаської області, спеціаліст вищої категорії
Контрольна робота 1. Степенева функція
І варіант
-
Знайдіть область визначення функції:
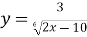 .
.
А) ![]() ; Б)
; Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]()
2. Обчисліть: ![]() .
.
А) -7; Б) 3; В) -3; Г) 7; Д) 5 .
3. Установіть відповідність між виразами (1-4) і числами (А-Д), одержаними в результаті їх перетворення:
1) ![]() А) 12;
А) 12;
2) ![]() Б) 1;
Б) 1;
3) ![]() В) 48;
В) 48;
4) ![]() . Г) -1;
. Г) -1;
Д) 2.
4. Установіть відповідність між виразами (1-4) і виразами (А -Д), одержаними в результаті їх перетворення:
1) ![]() А)
А) ![]() ;
;
2) ![]() Б)
Б) ![]()
3) ![]() В)
В) ![]() ;
;
4) ![]() . Г)
. Г) ![]()
Д) ![]() .
.
5. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
6. Обчисліть значення виразу: 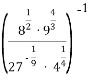 .
.
7. Знайдіть область визначення функції:
![]() .
.
8. Розв’яжіть рівняння : ![]() .
.
9. Спростіть вираз: ![]() .
.
ІІ варіант
-
Знайдіть область визначення функції:
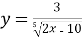 .
.
А) ![]() ; Б)
; Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]() .
.
2. Обчисліть: ![]()
А) -7; Б) 1; В) -1; Г) 7; Д) 12.
3. Установіть відповідність між виразами (1-4) і числами (А-Д), одержаними в результаті їх перетворення:
1) ![]() А) 1;
А) 1;
2) ![]() Б) 2;
Б) 2;
3) ![]() В) 4;
В) 4;
4) ![]() . Г) 3;
. Г) 3;
Д) 6.
4. Установіть відповідність між виразами (1-4) і виразами (А-Д), одержаними в результаті їх перетворення:
1) ![]() А)
А) ![]() ;
;
2) ![]() Б)
Б) ![]()
3) ![]() В)
В) ![]() ;
;
4) ![]() . Г)
. Г) ![]()
Д) ![]() .
.
5. Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() .
.
6. Обчисліть значення виразу: 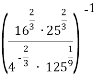 .
.
7. Знайдіть область визначення функції:
![]() .
.
8. Розв’яжіть рівняння : ![]() .
.
9. Спростіть вираз: ![]() .
.
Контрольна робота 2 . Тригонометричні функції
І варіант
- Кутом якої чверті є кут, радіанна міра якого дорівнює 1,5 радіана ?
А) І; Б) ІІ; В) ІІІ; Г) IV; Д) визначити неможливо.
-
Знайдіть значення виразу:
 .
.
А) ![]() ; Б)
; Б) ![]() ; В) 0 ; Г) 1; Д)
; В) 0 ; Г) 1; Д) ![]() .
.
- Укажіть неправильну нерівність:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Відомо, що
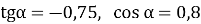 . Знайдіть
. Знайдіть 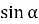 .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() .
.
- Установіть відповідність між функцією, заданою формулою (1-3), та її властивістю (А-Г):
-
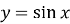 ; А) функція не має найбільшого значення;
; А) функція не має найбільшого значення;
-
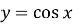 ; Б) функція є зростаючою на всій області визначення;
; Б) функція є зростаючою на всій області визначення;
-
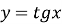 ; В) найбільше значення функції дорівнює 1 при
; В) найбільше значення функції дорівнює 1 при 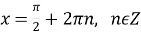 ;
;
Г) функція парна.
-
Знайдіть головний період функції:
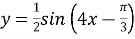 .
.
-
Доведіть парність функції:
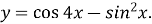
-
Знайдіть значення виразу:
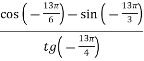 .
.
-
Побудуйте графік функції: а)
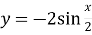 ; б)
; б) 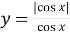 .
.
ІІ варіант
- Кутом якої чверті є кут, радіанна міра якого дорівнює 2,5 радіана?
А) І; Б) ІІ; В) ІІІ; Г) IV; Д) визначити неможливо.
-
Знайдіть значення виразу:
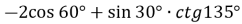 .
.
А) ![]() ; Б)
; Б) ![]() ; В) 0; Г) 1; Д)
; В) 0; Г) 1; Д) ![]() .
.
- Укажіть неправильну нерівність:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Відомо, що
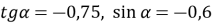 . Знайдіть
. Знайдіть 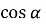 .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() .
.
- Установіть відповідність між функцією, заданою формулою (1-3), та її властивістю (А-Г):
1) ![]() ; А) функція не має найменшого значення;
; А) функція не має найменшого значення;
2) ![]() ; Б) функція є спадною на всій області визначення;
; Б) функція є спадною на всій області визначення;
3) ![]() . В) найменше значення функції дорівнює -1 при
. В) найменше значення функції дорівнює -1 при ![]() ;
;
Г) функція зростає на проміжках ![]()
-
Знайдіть головний період функції :
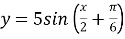 .
.
-
Доведіть непарність функції :
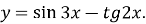
-
Знайдіть значення виразу:
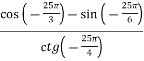 .
.
-
Побудуйте графік функції: а)
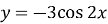 ; б)
; б) 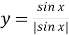 .
.
Контрольна робота 3 . Тригонометричні тотожності
І варіант
- Укажіть неправильну тригонометричну формулу:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Укажіть вираз, тотожно рівний виразу
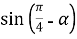 :
:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
- Установіть відповідність між тригонометричними виразами (1-4) і їхніми числовими значеннями (А-Д):
1) ![]() ; А)
; А) ![]() ;
;
2) ![]() ; Б)
; Б) ![]() ;
;
3) ![]() ; В) 1;
; В) 1;
4) ![]() . Г)
. Г) ![]() ;
;
Д) ![]() .
.
-
Обчисліть:
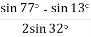 .
.
-
Спростіть вираз:
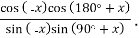
-
Знайдіть значення виразу:
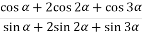 , якщо
, якщо 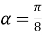 .
.
-
Спростіть вираз:
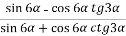 .
.
-
Знайдіть найбільше та найменше значення виразу:
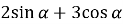 .
.
-
Доведіть тотожність: а)
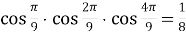 ;
;
б) ![]()
ІІ варіант
- Укажіть неправильну тригонометричну формулу:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Укажіть вираз, тотожно рівний виразу
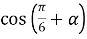 :
:
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
- Установіть відповідність між тригонометричними виразами (1-4) і їхніми числовими значеннями (А-Д):
1) ![]() ; А)
; А) ![]() ;
;
2) ![]() ; Б)
; Б) ![]() ;
;
3) ![]() ; В)
; В) ![]() ;
;
4) ![]() . Г)
. Г) ![]() ;
;
Д) 2.
-
Обчисліть:
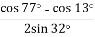 .
.
-
Спростіть вираз:
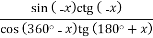 .
.
-
Знайдіть значення виразу:
 , якщо
, якщо 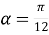 .
.
-
Спростіть вираз:
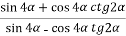 .
.
-
Знайдіть найбільше та найменше значення виразу:
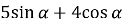 .
.
-
Доведіть тотожність: а)
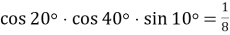 .
.
б) ![]()
Контрольна робота 4 . Тригонометричні рівняння
І варіант
-
Обчисліть:
 .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() .
.
- Установіть відповідність між рівняннями (1-4) і множинами їхніх розв’язків (А-Д):
1) ![]() ; А)
; А) ![]() ;
;
2) ![]() ; Б) розв’язків немає;
; Б) розв’язків немає;
3) ![]() ; В)
; В) ![]() ;
;
![]() . Г)
. Г) ![]() ;
;
Д) ![]() .
.
-
Знайдіть найменший додатний корінь рівняння:
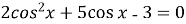 .
.
-
Розв’яжіть рівняння
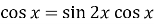 способом розкладання на множники .
способом розкладання на множники .
-
Розв’яжіть однорідне рівняння:
 .
.
-
Розв’яжіть рівняння:
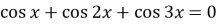 .
.
-
Розв’яжіть рівняння : а)
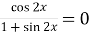 ;
;
б) ![]() .
.
-
Розв’яжіть систему рівнянь:
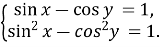
-
Визначте, при яких значеннях параметра
 рівняння
рівняння 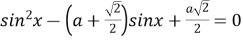 має на проміжку
має на проміжку 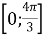 : 1) два корені; 2) три корені; 3) не менше ніж три корені?
: 1) два корені; 2) три корені; 3) не менше ніж три корені?
ІІ варіант
-
Обчисліть:
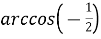 .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() .
.
- Установіть відповідність між рівняннями (1-4) і множинами їхніх розв’язків (А-Д):
1) ![]() ; А)
; А) ![]() ;
;
2) ![]() ; Б) розв’язків немає ;
; Б) розв’язків немає ;
3) ![]() ; В)
; В) ![]() ;
;
-
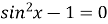 . Г)
. Г) 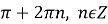 ;
;
Д) ![]() .
.
-
Знайдіть найменший додатний корінь рівняння :
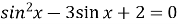 .
.
-
Розв’яжіть рівняння
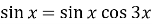 способом розкладання на множники .
способом розкладання на множники .
-
Розв’яжіть однорідне рівняння :
 .
.
-
Розв’яжіть рівняння:
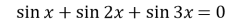 .
.
-
Розв’яжіть рівняння: а)
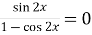 ;
;
б) ![]()
-
Розв’яжіть систему рівнянь:
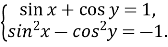
-
Визначте, при яких значеннях параметра
 рівняння
рівняння 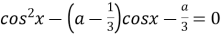 має на проміжку
має на проміжку 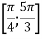 : 1) два корені; 2) три корені; 3) не менше ніж три корені?
: 1) два корені; 2) три корені; 3) не менше ніж три корені?
Контрольна робота 5. Тригонометричні нерівності
І варіант
-
Розв’яжіть нерівність:
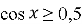 .
.
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Розв’яжіть нерівність:
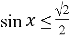 .
.
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Розв’яжіть нерівність:
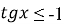 .
.
А) ![]()
![]() ;
;
Б) ![]() ;
;
В) ![]()
![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
- Установіть відповідність між заданою нерівністю (1-3) та її розв’язками (А-Г):
![]() А)
А) ![]() ;
;
![]() Б)
Б) ![]() ;
;
3) ![]() . В)
. В) ![]() ;
;
Г) ![]() .
.
Д) ![]() .
.
-
Знайдіть область визначення функції :
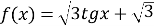 .
.
-
Розв’яжіть нерівність: а)
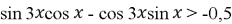 ;
;
б) ![]() ;
;
в) ![]() .
.
-
Розв’яжіть нерівність:
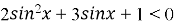 .
.
-
Розв’яжіть нерівність:
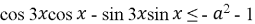 .
.
ІI варіант
-
Розв’яжіть нерівність:
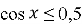 .
.
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Розв’яжіть нерівність:
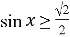 .
.
А) ![]() ;
;
Б) ![]() ;
;
В) ![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
-
Розв’яжіть нерівність:
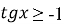 .
.
А) ![]()
![]() ;
;
Б) ![]() ;
;
В) ![]()
![]() ;
;
Г) ![]() ;
;
Д) ![]() .
.
- Установіть відповідність між заданою нерівністю (1-3) та її розв’язками (А-Г):
1) ![]() ; А)
; А) ![]() ;
;
2) ![]() ; Б)
; Б) ![]() ;
;
3) ![]() . В)
. В) ![]() ;
;
Г) ![]() .
.
Д) ![]() .
.
-
Знайдіть область визначення функції :
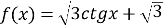 .
.
-
Розв’яжіть нерівність : а)
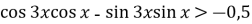 ;
;
б) ![]() ;
;
в) ![]() .
.
-
Розв’яжіть нерівність:
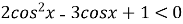 .
.
-
Розв’яжіть нерівність:
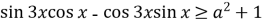 .
.
Контрольна робота 6. Границя та неперервність функції
Варіант 1
- Чи є функція неперервною в кожній точці проміжку:
а) ![]()
б) ![]()
в) ![]()
- Обчисліть границю функції:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
е) ![]() .
.
-
Доведіть, що функція
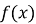 неперервна в точці
неперервна в точці 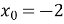 :
:
![]()
- Серед даних функцій виберіть ті, графіки яких мають вертикальні асимптоти, горизонтальні асимптоти, похилі асимптоти:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
- Знайдіть асимптоти графіка функції (якщо вони існують):
а) ![]()
б) ![]()
-
При яких значеннях
 функція
функція 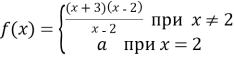 неперервна в точці
неперервна в точці 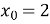 ?
?
-
Побудуйте графік функції
 дослідіть цю функцію на неперервність у точках
дослідіть цю функцію на неперервність у точках 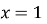 і
і 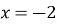 .
.
-
При яких значеннях параметра
 функція
функція 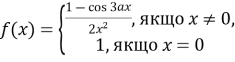 є неперервною в точці
є неперервною в точці 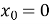 ?
?
Варіант 2
- Чи є функція неперервною в кожній точці проміжку:
а) ![]()
б) ![]()
в) ![]() ?
?
- Обчисліть границю функції:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
е) ![]() .
.
-
Доведіть, що функція
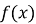 неперервна в точці
неперервна в точці 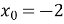 :
:
![]()
- Серед даних функцій виберіть ті, графіки яких мають вертикальні асимптоти, горизонтальні асимптоти, похилі асимптоти:
а) ![]()
б) ![]()
в) ![]()
г) ![]()
- Знайдіть асимптоти графіка функції (якщо вони існують):
а) ![]()
б) ![]()
-
При яких значеннях
 функція
функція 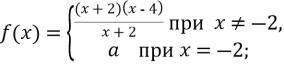 неперервна в точці
неперервна в точці 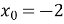 ?
?
-
Побудуйте графік функції
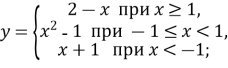 дослідіть цю функцію на неперервність у точках
дослідіть цю функцію на неперервність у точках 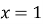 і
і 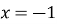 .
.
-
При яких значеннях параметра
 функція
функція 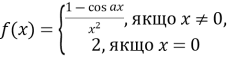 є неперервною в точці
є неперервною в точці 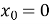 ?
?
Контрольна робота 7. Похідна функції
Варіант 1
-
Знайдіть тангенс кута нахилу дотичної до графіка функції
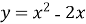 в точці з абсцисою
в точці з абсцисою 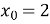 .
.
А) -1![]() ; Б) 1; В) 0; Г) 2; Д) -2.
; Б) 1; В) 0; Г) 2; Д) -2.
-
Тіло рухається прямолінійно за законом
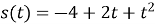 (
(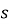 вимірюється в метрах,
вимірюється в метрах,  у секундах). Знайдіть швидкість цього тіла в момент часу
у секундах). Знайдіть швидкість цього тіла в момент часу 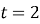 с.
с.
А) 1 м/с; Б) 8 м/с; В) 4 м/с; Г) 2 м/с; Д) 6 м/с.
- Установіть відповідність між функціями (1-4) та їх похідними (А-Д):
-
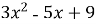 ; А)
; А) 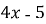 ;
;
-
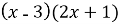 ; Б)
; Б) 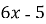 ;
;
-
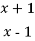 ; В)
; В) 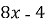 ;
;
-
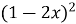 . Г)
. Г) 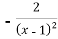 ;
;
Д) ![]() .
.
- Знайдіть похідну функції:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
- Знайдіть похідну складеної функції:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
-
Запишіть рівняння дотичних до графіка функції
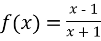 , якщо дотичні паралельні прямій
, якщо дотичні паралельні прямій 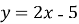 .
.
-
Матеріальна точка рухається за законом
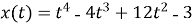 (
(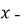 в метрах,
в метрах, 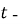 у секундах). Визначте швидкість точки в момент, коли її прискорення мінімальне.
у секундах). Визначте швидкість точки в момент, коли її прискорення мінімальне.
-
Знайдіть значення
 і
і 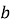 , за яких виконуються умови:
, за яких виконуються умови: 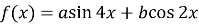 ,
, 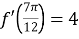 ,
, 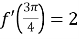 .
.
Варіант 2
-
Знайдіть тангенс кута нахилу дотичної до графіка функції
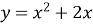 в точці з абсцисою
в точці з абсцисою 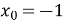 .
.
А) ![]() ; Б) 1; В) -1; Г) 4; Д) -3.
; Б) 1; В) -1; Г) 4; Д) -3.
-
Тіло рухається прямолінійно за законом
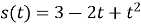 (
(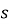 вимірюється в метрах,
вимірюється в метрах,  у секундах). Знайдіть швидкість цього тіла в момент часу
у секундах). Знайдіть швидкість цього тіла в момент часу 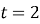 с.
с.
А) 3 м/с; Б) 2 м/с; В) 5 м/с; Г) 1 м/с; Д) 4 м/с.
- Установіть відповідність між функціями (1-4) та їх похідними (А-Д):
-
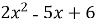 А)
А) 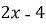 ;
;
-
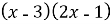 Б)
Б) 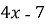 ;
;
-
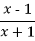 В)
В) 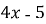 ;
;
-
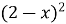 Г)
Г) 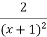 ;
;
Д) ![]() .
.
- Знайдіть похідну функції:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
- Знайдіть похідну складеної функції:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
-
Запишіть рівняння дотичних до графіка функції
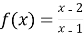 , якщо дотичні паралельні прямій
, якщо дотичні паралельні прямій 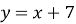 .
.
-
Матеріальна точка рухається за законом
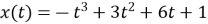 (
(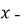 в метрах,
в метрах, 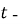 у секундах). Визначте прискорення точки в момент, коли її швидкість максимальна.
у секундах). Визначте прискорення точки в момент, коли її швидкість максимальна.
-
Знайдіть значення
 і
і 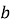 , за яких виконуються умови:
, за яких виконуються умови: 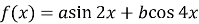 ,
, 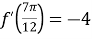 ,
, 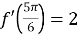 .
.
Контрольна робота 8. Застосування похідної
Варіант 1
-
Укажіть абсцису точки, у який дотична до графіка функції
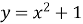 паралельна осі абсцис, якщо така точка існує.
паралельна осі абсцис, якщо така точка існує.
А) 0; Б) 1; В) -1; Г) 2; Д) таких точок немає.
-
Знайдіть проміжки зростання функції
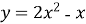 .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]() .
.
-
Укажіть усі критичні точки функції
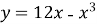 .
.
А) 0; 2; Б) 0; ![]() ; В) 2; Г) 0; Д) 2; -2.
; В) 2; Г) 0; Д) 2; -2.
-
Знайдіть найбільше значення функції
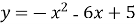 на проміжку
на проміжку 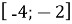 .
.
-
У якій точці кривої
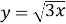 дотична нахилена до осі абсцис під кутом
дотична нахилена до осі абсцис під кутом 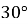 ?
?
-
Висота, на якій перебуває камінь, що кинули вертикально вгору зі швидкістю
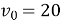 м/с із початкової висоти
м/с із початкової висоти 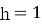 м, змінюється за законом
м, змінюється за законом 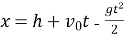 (
( 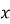 вимірюється в метрах,
вимірюється в метрах, 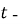 у секундах). На якій висоті швидкість каменю дорівнюватиме нулю (вважайте, що прискорення вільного падіння
у секундах). На якій висоті швидкість каменю дорівнюватиме нулю (вважайте, що прискорення вільного падіння 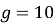 м/с)?
м/с)?
-
Дослідіть функцію
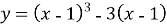 і побудуйте її графік.
і побудуйте її графік.
-
У прямокутний трикутник, гіпотенуза якого дорівнює 24 см, а кут -
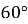 , вписано прямокутник так, що одна його сторона лежить на гіпотенузі. Знайдіть сторони прямокутника, якщо відомо, що він має найбільшу площу.
, вписано прямокутник так, що одна його сторона лежить на гіпотенузі. Знайдіть сторони прямокутника, якщо відомо, що він має найбільшу площу.
-
Скільки коренів має рівняння
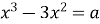 при умові
при умові 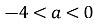 ?
?
Варіант 2
-
Укажіть абсцису точки, у який дотична до графіка функції
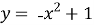 паралельна осі абсцис, якщо така точка існує.
паралельна осі абсцис, якщо така точка існує.
А) 1; Б) 2; В) -1; Г) 0; Д) таких точок немає.
-
Знайдіть проміжки зростання функції
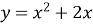 .
.
А) ![]() ; Б)
; Б) ![]() ; В)
; В) ![]() ; Г)
; Г) ![]() ; Д)
; Д) ![]()
-
Укажіть усі критичні точки функції
 .
.
А) ![]() ; Б)
; Б) ![]() ; В) 1; Г) 0; Д) 3.
; В) 1; Г) 0; Д) 3.
-
Знайдіть найбільше значення функції
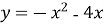 на проміжку
на проміжку 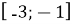 .
.
-
У якій точці кривої
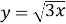 дотична нахилена до осі абсцис під кутом
дотична нахилена до осі абсцис під кутом 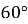 ?
?
-
Висота, на якій перебуває камінь, що кинули вертикально вгору зі швидкістю
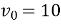 м/с із початкової висоти
м/с із початкової висоти 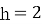 м, змінюється за законом
м, змінюється за законом 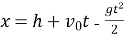 (
( 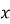 вимірюється в метрах,
вимірюється в метрах, 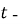 у секундах). На якій висоті швидкість каменю дорівнюватиме нулю (вважайте, що прискорення вільного падіння
у секундах). На якій висоті швидкість каменю дорівнюватиме нулю (вважайте, що прискорення вільного падіння 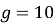 м/с)?
м/с)?
-
Дослідіть функцію
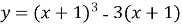 і побудуйте її графік.
і побудуйте її графік.
-
У прямокутний трикутник, гіпотенуза якого дорівнює 24 см, а кут -
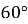 , вписано прямокутник так, що його кут збігається з прямим кутом трикутника. Знайдіть сторони прямокутника, якщо відомо, що він має найбільшу площу.
, вписано прямокутник так, що його кут збігається з прямим кутом трикутника. Знайдіть сторони прямокутника, якщо відомо, що він має найбільшу площу.
-
Скільки коренів має рівняння
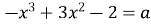 при умові
при умові 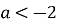 ?
?
Література:
- Каплун О. І. Алгебра і початки аналізу. Геометрія. 10 клас: зошит для поточного та тематичного оцінювання / Каплун О. І. – Харків.: ПЕТ, 2014. – 128 с. +32 с. вкладка.
- Гальперіна А. Р. Алгебра і початки аналізу. Геометрія. 10 клас. Академічний рівень. Тестовий контроль знань / А. Р. Гальперіна . – 2-ге вид. – Київ.: Літера ЛТД, 2013. – 128с.
- Єршова А. П. Самостійні та контрольні роботи з алгебри та початків аналізу для 10-11 класу. Різнорівневі дидактичні матеріали / Єршова А.П., Голобородько В. В. – Харків.: Гімназія, 2004. -176 с.


про публікацію авторської розробки
Додати розробку

-

Мисік Марина Олександрівна
16.12.2020 в 07:44
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Жабровець Олег Валентинович
19.09.2019 в 21:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Marinov Alex
13.06.2019 в 06:59
Непогана робота!
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Івасюнько Майя Юріївна
24.05.2019 в 00:04
Дякую, ваша збірка дуже мені допомогла!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук