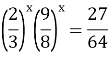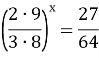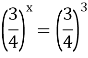Урок "Показникові рівняння"
Тема: ПОКАЗНИКОВІ РІВНЯННЯ
Мета уроку: познайомити з новим видом рівнянь – показниковим, показати способи розв’язання різних видів показникових рівнянь за алгоритмом.
Формування ключових компетентностей: формувати уміння грамотно висловлюватись рідною мовою, доречно та коректно вживати в мовленні математичну термінологію; застосовувати математичний апарат для розв’язання показникових рівнянь; усвідомлення значення математики для дослідження навколишнього світу; усвідомлення важливості математики як універсальної мови науки, техніки та технологій; уміння діяти за алгоритмом; усвідомлення важливості ІКТ для ефективного пошуку інформації та розв’язання математичних задач; самостійне опрацювання навчального матеріалу з математики; критично оцінювати власні досягнення; усвідомлювати важливість самоосвіти для успішного життя; уміння виявляти ініціативу та відповідальність під час групової роботи .
Тип уроку: комбінований
Обладнання: презентація, учнівська презентація, робочий зошит, інтерактивні вправи «Знайди пару», «Хмара» та «Пазл», учнівський плакат, ватмани, маркери, Google-тест (вхідний)
Структура заняття
|
№ |
Елемент уроку |
Час, хв. |
|
І. |
Організаційний момент |
1 |
|
ІІ. |
Перевiрка домашнього завдання |
6 |
|
ІІІ. |
Мотивація навчальної дiяльностi |
2 |
|
IV. |
Актуалізація і корекція опорних знань |
4 |
|
V. |
Виклад нового матеріалу |
17 |
|
VI. |
Закріплення отриманих знань |
7 |
|
VIІ. |
Узагальнення та систематизація знань |
5 |
|
VIII. |
Підведення підсумків уроку. Оцінювання. Повідомлення домашнього завдання |
3 |
Хід уроку
- Організаційний момент (привітання, перевірка відсутніх)
Діти сідають за парти (парти розташовані так, що утворюється 3 груп і кожному учневі зручно дивитися на дошки: крейдову та мультимедійну)
Викладач. На столах ви бачите робочий зошит, який ви будете заповнювати протягом уроку. Вверху сторінки є шкала оцінювання, вона накопичувальна. Протягом уроку ви самостійно будете собі виставляти зароблені бали за виконану роботу й підведете підсумки власної активності наприкінці уроку.
|
Домашнє завдання |
Знайди пару |
Дешиф-ровщик |
Робота в групі |
Хмара |
Пазл |
Сума |
|
до 6 балів тесту – 1 бал, 7-12 балів – 2 бали |
1бал |
1-2 бали за швидкість |
1-3 бали за швидкість |
1 бал |
1 бал |
|
|
|
|
|
|
|
|
|
- Перевірка домашнього завдання
- Який розділ ми почали вивчати минулого уроку?
- Тема минулого уроку?
Оголошення результатів проходження Google-тесту (домашнє завдання) шляхом виводу таблиці оцінювання на екран. Тест розміщений на блозі викладача: http://matematuka-bcpto.blogspot.com Творче завдання: дослідити та виявити ті області й галузі наук де можна безпосередньо побачити застосування показникової функції.
- Мотивація навчальної діяльності
Застосування показникової функції досить широке: фізика, хімія, медицина, економіка, екологія, географія та ще цілий ряд наук. Сьогодні ми продовжуємо вивчення розділу «Показникова функція» й познайомимося з вами з новим видом рівнянь, які обов’язково входять до завдань ЗНО (зовнішнє незалежне оцінювання) на рівні з квадратними, ірраціональними та тригонометричними. Вони мають назву – показникові.
Запис у робочих зошитах тему уроку.
- Актуалізація і корекція опорних знань
Фронтальне опитування
- Який вид має показникова функція?
- Назвіть область визначення показникової функції?
- Назвіть область значень показникової функції?
- Назвіть координати точки, через яку проходить кожна показникові функція?
- За якої умови показникова функція зростає? Спадає?
- Як називається графік показникової функції?
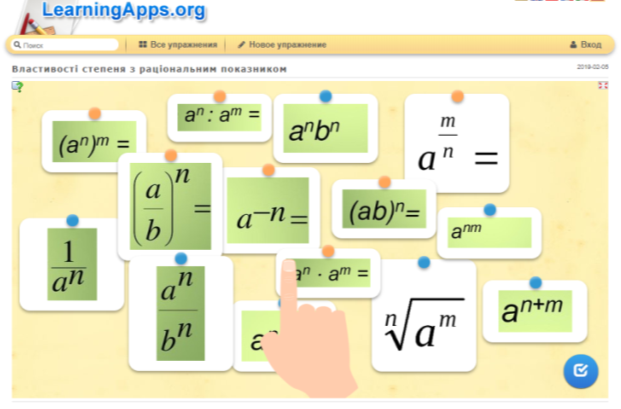 Інтерактивна вправа «Знайди пару» з теми «Властивості степеню з раціональним показником» (Учні по черзі виходять до дошки. За правильну відповідь отримують один бал й записують до шкали оцінювання)
Інтерактивна вправа «Знайди пару» з теми «Властивості степеню з раціональним показником» (Учні по черзі виходять до дошки. За правильну відповідь отримують один бал й записують до шкали оцінювання)
- Виклад нового матеріалу.
Показниковими називають рівняння, в яких невідоме (змінна) входить лише у показник степеня (а основа цього степеня не містить змінної).
Розглянемо найпростіше показникове рівняння ![]() , де
, де ![]() ,
, ![]() . Оскільки множина значень функції – множина додатних чисел, то дане рівняння
. Оскільки множина значень функції – множина додатних чисел, то дане рівняння ![]() :
:
-
має єдиний корінь, якщо
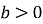 ;
;
-
не має коренів, якщо
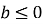 .
.
Щоб знайти єдиний корінь при ![]() , досить подати
, досить подати ![]() у вигляді
у вигляді ![]() . Очевидно, що
. Очевидно, що ![]() .
.
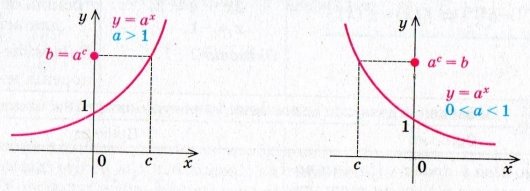 Графічно це проілюстровано на рисунку.
Графічно це проілюстровано на рисунку.
Наприклад, щоб розв’язати рівняння ![]() =49, досить подати це рівняння у вигляді
=49, досить подати це рівняння у вигляді ![]() і записати його єдиний корінь х=2.
і записати його єдиний корінь х=2.
Розглянемо інше рівняння: ![]() . Дане рівняння не має коренів, оскільки
. Дане рівняння не має коренів, оскільки ![]() завжди більше нуля. Це наглядно ви можете побачити на графіках.
завжди більше нуля. Це наглядно ви можете побачити на графіках.
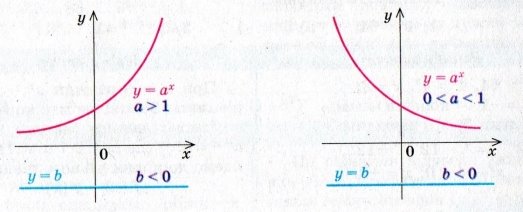
Узагальнюючи наведені вище міркування стосовно розв’язування найпростіших показникових рівнянь, відзначимо, що при ![]() ,
, ![]() рівняння:
рівняння: ![]() , рівносильно рівнянню
, рівносильно рівнянню ![]()
Запишемо коротко це в зошитах: ![]()
Найпоширенішим способом розв’язування показникових рівнянь є зведення до однієї основи, використовуючи основні формули дій над степенями, які ми щойно повторили.
Розглянемо приклад: ![]()
Вправа «Дешифровщик» ( учні розподілені на три групи, кожна з яких отримує свій перелік найпростіших показникових рівнянь. Отримавши корінь рівняння, необхідно знайти букву, яка відповідає даному кореню й вписати її до аркуша під номером самого рівняння).
На виконання завдання 2-3 хвилини. Команда, що справиться першою, отримує додатковий бал.
|
а |
в |
г |
д |
е |
л |
м |
щ |
п |
р |
с |
ц |
ь |
я |
! |
|
0 |
-3 |
5 |
3 |
-2 |
-1 |
2 |
4 |
-5 |
6 |
1 |
-4 |
7 |
8 |
|
Перша група
- 42x-3=4
- 5x-2=25
-
(
 )x=7
)x=7
-
(
 )x=
)x=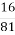
- 3x=27
- 74x+8=1
-
3x=
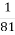
-
619-3x=
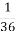
(Молодець)
Друга група
-
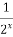 =32
=32
- 9-x=81
- 10x=1000000
-
(
 )x=
)x=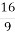
-
(
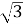 )x=3
)x=3
- 3x-1=27
- 5x-3=25
- 4x=1
(Перемога)
Третя група
-
63x+7=
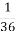
- 4x=64
- 12x=1
-
(
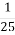 )x=25
)x=25
- 2x=16
- 3x=3
- 23(x-6)=64
- 6x+3=-36
(Вдалося!)
Викладач. Ми розглянули найпростіші рівняння. Загального методу розв’язання показникових рівнянь немає. Можна виділити кілька видів показникових рівнянь і навести способи їх розв’язання.
Найпоширеніший спосіб – спосіб зведення до спільної основи (використовуючи властивості степеня з раціональним показником)
|
|
Спосіб винесення спільного множника за дужки
|
|
Спосіб приведення рівняння до квадратного шляхом заміни змінної
|
|
Закріплення отриманих знань
Робота в групах
На столі у вчителя є 3 пронумерованих конверти із рівняннями. Представник групи підходить до столу і витягує конверт із завданням після чого групи починають розв’язувати запропоновані рівняння. Після того як рівняння будуть розв’язані, один учень з кожної групи представляє розв’язання рівняння на дошці (розв’язок записаний на аркуші з допомогою маркера), всі інші уважно слухають, виправляють помилки, якщо вони є, записують розв’язання завдань в зошит. На виконання завдання 3-4 хвилини.
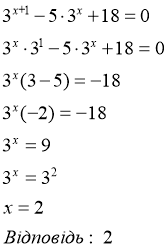 1.
1.
2.![]()
![]() =
= ![]() ;
;
![]() ;
;
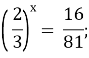
![]() ;
;
х = 4.
Відповідь. 4.
3. 4х + 32х – 4 = 0;
22х + 32х – 4 = 0;
Нехай 2х = t, 22х = t2;
t2 + 3t – 4 = 0;
D = 32 - 41 (- 4) = 25;
![]()
![]()
2х = 1; 2х = - 4;
2х = 20; розв’язків
х = 0. немає.
Відповідь. 0.
- Узагальнення і систематизація знань
Опитування (інтерактивна вправа Хмара)
- Яку тему ми вивчали на уроці?
- Дайте визначення показниковому рівнянню.
- Скільки способів розв’язання показникових рівнянь ми розглянули?
- Назвіть ці способи.
-
 Знання яких властивостей ми використовуємо при розв’язанні кожного з рівнянь?
Знання яких властивостей ми використовуємо при розв’язанні кожного з рівнянь?
- Знання якої теми знадобиться нам у рівнянні, що зводиться до квадратного шляхом заміни змінної?
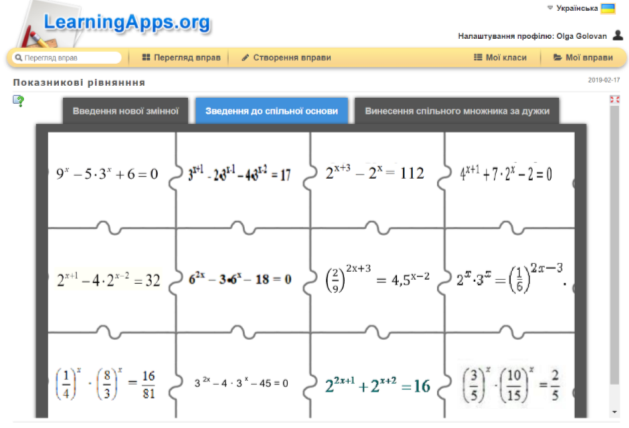 Інтерактивна вправа «Пазл» (поставити у відповідність рівняння та спосіб, яким його розв’язують)
Інтерактивна вправа «Пазл» (поставити у відповідність рівняння та спосіб, яким його розв’язують)
 Правильні відповіді відкривають пазл – отримуємо портрет відомого математики Леонарда Ейлера, який розробляв питання пов’язані з показниковою функцією. Йому належить відкриття зв’язку між показниковою та тригонометричною функціями. Також йому належить введення символу функції
Правильні відповіді відкривають пазл – отримуємо портрет відомого математики Леонарда Ейлера, який розробляв питання пов’язані з показниковою функцією. Йому належить відкриття зв’язку між показниковою та тригонометричною функціями. Також йому належить введення символу функції ![]() .
.
- Підведення підсумку уроку. Оцінювання. Домашнє завдання
(заключне слово, підрахунок оцінок, руки піднімають – хто заробив ? балів,
завдання домашнього завдання)
Домашнє завдання:
- Вивчити теоретичний матеріал (що таке показникові рівняння та алгоритм розв’язання різних видів)
- Розв’язати наступні різнорівневі рівняння (в допомогу презентація «Розвязання показникових рівнянь», розміщена на блозі http://matematuka-bcpto.blogspot.com )
-
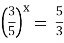 ; (1 бал)
; (1 бал)
-
0,7х = 2
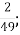 (1 бал)
(1 бал)
- 9-х = 27; (1 бал)
-
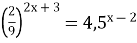 (2 бали)
(2 бали)
- 5х+1 + 5х = 150; (2 бали)
- 2х + 2х-3 = 18; (2 бали)
-
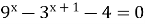 (3 бали)
(3 бали)


про публікацію авторської розробки
Додати розробку