КР "Інтеграл та його застосування"
Контрольная работа по теме «Интеграл и его применение»
Вариант 1
- (0.5 бал.)Указать общий вид первообразной для функции f (x) = sin 4 x.
|
А |
Б |
В |
Г |
Д |
|
|
|
4 cos 4x + c |
– 4 cos 4x + c |
– cos 4x + c |
2. (0.5 бал.) Вычислить: ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
9 |
3 |
26 |
27 |
6 |
3. (1 бал.) Указать первообразную для функции f (x) = 8х3, график которой проходит через точку А(1; 2).
|
А |
Б |
В |
Г |
Д |
|
F(x) = 2x4 |
F(x) = 2x4 – 1 |
F(x) = x4 + 1 |
F(x) = 24x2 – 22 |
F(x) = 2x4 + 1 |
4. (2 бал.)Установить соответствие между функциями (1 – 4) и их первообразной (А – Д).
|
1 |
у = |
А |
|
|
2 |
у = |
Б |
|
|
3 |
у = 7х |
В |
3х2 + с |
|
4 |
у = х7 |
Г |
7 |
|
|
|
Д |
|
5. (1 бал.)Найти площадь фигуры, ограниченую линиями: у = х3, у = 0, х = 2.
|
А |
Б |
В |
Г |
Д |
|
3 |
4 |
2 |
5 |
1 |
6. (4 бал.)Вычислить: 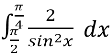 .
.
![]()
7. (3 бал.)Найти площадь фигуры, ограниченую линиями: у = 5 – х2, у = 3 – х.
Контрольная работа по теме «Интеграл и его применение»
Вариант 2
- (0.5 бал.)Указать общий вид первообразной для функции f (x) = cos 3 x.
|
А |
Б |
В |
Г |
Д |
|
|
|
3 sin 3x + c |
– 3 sin 3x + c |
sin 3x + c |
2. (0.5 бал.) Вычислить: ![]() .
.
|
А |
Б |
В |
Г |
Д |
|
24 |
16 |
4 |
8 |
6 |
3. (1 бал.) Указать первообразную для функции f(x) = 6 х5, график которой проходит через точку А(2; 65).
|
А |
Б |
В |
Г |
Д |
|
F(x) = x6 – 1 |
F(x) = x6 + 3 |
F(x) = 6x6 – 1 |
F(x) = 30x6 – 12 |
F(x) = x6 + 1 |
4. (2 бал.)Установить соответствие между функциями (1 – 4) и их первообразной (А – Д).
|
1 |
у = |
А |
|
|
2 |
у = |
Б |
|
|
3 |
у = 5х |
В |
3х2 + с |
|
4 |
у = х5 |
Г |
5 |
|
|
|
Д |
|
5. (1 бал.)Найти площадь фигуры, ограниченую линиями: у = х2, у = 0, х = 3.
|
А |
Б |
В |
Г |
Д |
|
9 |
4 |
8 |
5 |
1 |
6. (4 бал.)Вычислить: 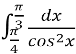 .
.
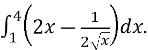
7. (3 бал.)Найти площадь фигуры, ограниченую линиями: у = 6 – х2, у = х + 4.

про публікацію авторської розробки
Додати розробку
