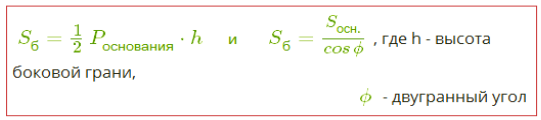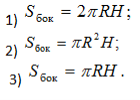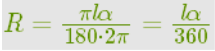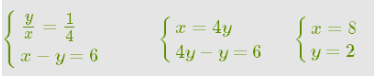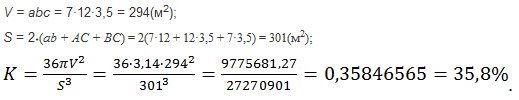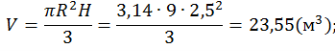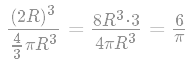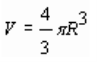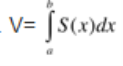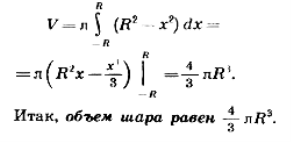Курс "Геометрия 11 класс"
«Геометрія 11 кл.»
Геометрия
11 клас
6 тем
Вольська Ірина Борисівна
вчитель математики , вища категорія
Оглавление
Словарь
Тема 1. Призма
1.1. Теория
• Теория.1. Призма и её элементы
• Теория.2. Параллелепипед
• Теория.3. Диагонали и диагональное сечение призмы
• Теория.4. Формула диагонали прямоугольного параллелепипеда
• Теория.5. Углы, образованные диагоналями призмы и её гранями
• Теория.6. Площадь поверхности и обьём призмы
1.2. Онлайн -ресурсы
• Онлайн калькулятор. Площадь прямоугольного параллелепипеда.
• Онлайн калькулятор. Площадь куба.
• Онлайн калькулятор. Объем призми.
• Онлайн калькулятор. Объём параллелепипеда
• Онлайн калькулятор. Объем прямоугольного параллелепипеда
• Онлайн калькулятор. Объем куба.
• Видеоурок : Объем прямоугольного параллелепипеда
• Видеоурок: Объем прямой призмы
• Видеоурок: Объем наклонной призмы
• Видеолекция «Параллелепипед и куб»
• Тест: «Параллелепипед и куб»
1.3. Урок
• Урок Объем прямоугольного параллелепипеда
1.4. Тест
• Тест по теме: « Призма»
Тема 2 . Пирамида
2.1. Теория
• Теория.1. Пирамида
• Теория.2. Правильная пирамида
• Теория.3. Пирамида с равными боковыми рёбрами
• Теория.4.Пирамиды с равными двугранными углами при основании
• Теория.5. Пирамида с боковым ребром, перпендикулярным плоскости основания
• Теория.6. Усеченная пирамида
2.2. Онлайн -ресурсы
• Онлайн калькулятор. Объем пирамиды .
• Онлайн калькулятор. Объем правильного тетраедра.
• Видеоурок: Объем пирамиды
• Видеоурок 2: Объем пирамиды
• Видеолекция «Пирамида»
• Тест "Пирамида"
2.3. Урок
• Урок; Объём пирамиды (решение прикладных задач
2.4. Тест
• Тест по теме: "Пирамида"
Тема 3. Цилиндр
3.1. Теория
• Теория 1.Цилиндр
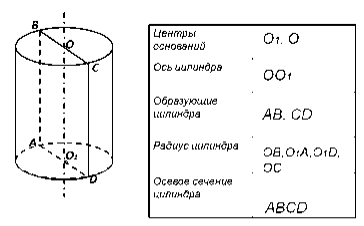
• Теория 2.Осевое сечение цилиндра
• Теория 3.Сечение цилиндра плоскостью
• Теория 4. Общее описание комбинаций геометрических тел
• Теория 5. Призма, вписанная в цилиндр
• Теория 6. Призма, описанная около цилиндра
• Теория 7.Объем и площадь поверхности цилиндра
3.2. Онлайн -ресурсы
• Онлайн калькулятор. Площадь цилиндра.
• Онлайн калькулятор. Объем цилиндра .
• Видеоурок: Объем цилиндра
• Видеолекция «Цилиндр»
• Тест "Цилиндр"
3.3. Урок
• Урок "Тела вращения. Цилиндр"
3.4. Тест
• Тест по теме: « Цилиндр»
3.5. Практическая работа
- Практическая работа по теме « Объём цилиндра »
Тема 4. Конус
4.1. Теория
• Теория 1.Элементы конуса
• Теория 2.Осевое сечение конуса
• Теория 3 .Выражение радиуса конуса из развёртки боковой поверхности конуса
• Теория 4.Цилиндр, описанный около конуса
• Теория 5. Цилиндр, вписанный в конус
• Теория 6. Пирамида, описанная около конуса
• Теория 7 . Пирамида, вписанная в конус
• Теория 8. Площадь поверхности и объём конуса
• Теория 9. Усечённый конус
4.2. Онлайн -ресурсы
• Онлайн калькулятор. Площадь поверхности конуса
• Онлайн калькулятор.Объем конуса.
• Видеоурок: Объем конуса
• Видеолекция «Конус»
• Тест "Конус"
4.3. Урок
• Урок Объём конуса.
4.4. Тест
• Тест по теме: « Конус»
4.5. Практическая работа
- Практическая работа по теме « Объём конуса »
Тема 5. Шар
5.1. Теория
• Теория 1 Шар, сфера
• Теория 2 Сечение шара плоскостью
• Теория 3 Шар, вписанный в цилиндр
• Теория 4 Шар, описанный около цилиндра
• Теория 5 Шар, описанный около конуса
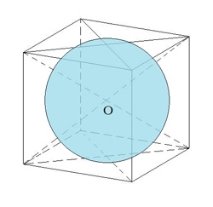
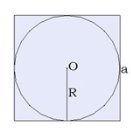
• Теория 6 Шар, вписанный в куб
• Теория 7 Шар, описанный около куба
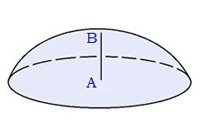
• Теория 8 Шаровой сегмент.
5.2. Онлайн -ресурсы
• Онлайн калькулятор. Площадь шара.
• Онлайн калькулятор. Объем шара
• Видеоурок: Площадь сферы
• Видеоурок: Объем шара
• Видеоурок: Объем шарового сегмента, шарового слоя, шарового сектора
• Видеолекция «Шар и сфера»
• Тест "Шар"
5.3. Урок
• Урок: "Объем шара".
5.4. Практическая работа
- Практическая работа по теме « Объём шара »
Тема 6. Итоговый урок
6.1. Урок: Решение практических задач на вычисление объёмов тел вращения.
6.2. Зачетная работа
6.3. Практическая работа
- Практическая работа по теме «Тела вращения»
6.4 . Урок-зачет по теме «Объемы тел»
• Урок-зачет
Аннотация
Дистанционное обучение — совокупность технологий, обеспечивающих доставку обучаемым основного объема изучаемого материала, интерактивное взаимодействие обучаемых и преподавателей в процессе обучения, предоставление обучаемым возможности самостоятельной работы по освоению изучаемого материала, а также в процессе обучения.
Цели курса: оказать помощь учащимся 10-11 классов и в подготовке к урокам, подготовить учащихся к сдаче экзамена в соответствии с требованиями, предъявляемыми образовательными стандартами.
Воспитательное назначение курса: обучение потребует от учащихся умственных и волевых усилий, развитого внимания, воспитания таких качеств, как активность, творческая инициатива, умений познавательного труда.
Задачи: повторить и обобщить знания по геометрия за курс основной школы;расширить знания по отдельным темам курса геометрия 10-11 клас; повысить уровень своей математической культуры, творческого развития, познавательной активности; познакомиться с возможностями использования электронных средств обучения, в том числе Интернет-ресурсов, в ходе подготовки к итоговой аттестации.
В предложенных 6 темах расматривается теоретический материал, практические задания для закрепления полученных теоретических знаний на практике, тестовые и 4 практические работы. Каждая практическая работа состоит из двух равносильных по степени сложности вариантов и сопровождается кратким теоретическим материалом, таблицами. Также представлены задачи для самостоятельного решения разного уровня сложности
Курс предназначен для учащихся вечерних школ, которые изучают геометрию в 10-12 классах по учебным планам общеобразовательных учебных заведений III степени
Апофема – это отрезок (а также его длина) перпендикуляра а, опущенного из центра правильного многоугольника на любую из его сторон
Диагональ - отрезок прямой линии, соединяющий две вершины многоугольника, не лежащие на одной стороне, или две вершины многогранника, не лежащие на одной грани.
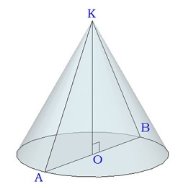
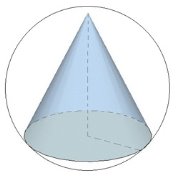
Конус - тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
Куб – правильный многогранник, каждая грань которого представляет собой квадрат.
Объём, одна из основных величин, связанных с геометрическими телами. В простейших случаях измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины.
Параллелепипед - это четырёхугольная призма, все грани которой являются параллелограммами.
Пирамидой называется многогранник, одна грань которого является n-угольником, а остальные грани - треугольники с общей вершиной
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры, неформально говоря, показывающая размер этой фигуры.
Призма - это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани - параллелограммами.
Поверхность шара называется сферой.
Угол - геометрическая фигура, состоящая из двух лучей с общим началом.
Усечённой пирамидой называется часть пирамиды между её основанием и плоскостью, параллельной ему.
Усечённый конус - тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны
Цилиндр - тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Шаровой сектор — это часть шара, ограниченная кривой поверхностью шарового сегмента и конической поверхностью основанием которой служит основание сегмента, а вершиной — центр шара.
Шаровой слой — это часть шара, заключенная между двумя секущими параллельными плоскостями.
|
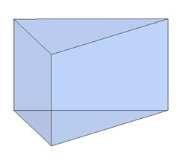
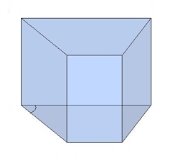
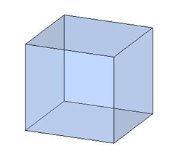
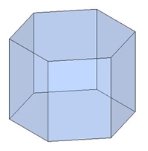
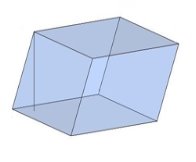
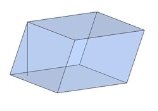
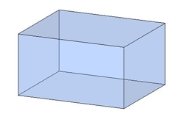
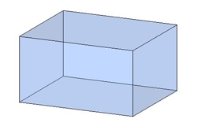
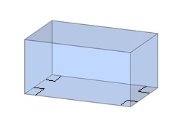
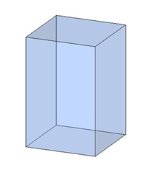
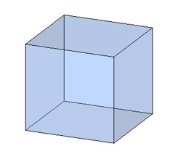
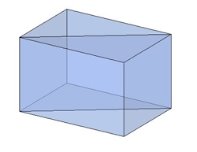
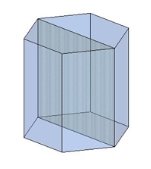
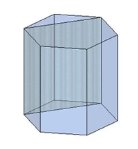
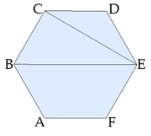
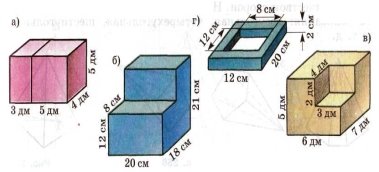
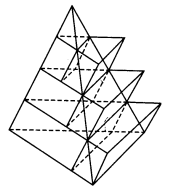
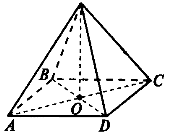
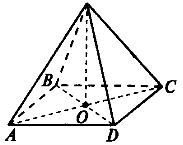
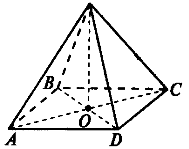
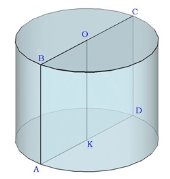
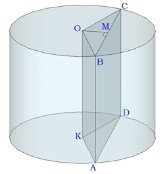
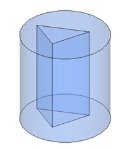
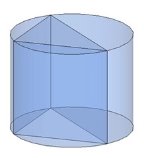
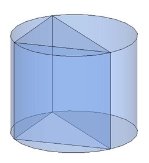
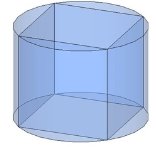
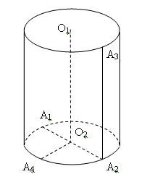
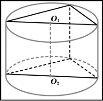
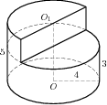
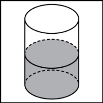
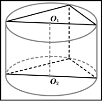
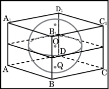
Тема 1. Призма Цель: Сформировать представление о многогранники. Изучить определение призмы и параллелепипеда и их элементов. Научиться строить изображения многогранников. Научиться решать задачи с использованием призм и параллелепипедов. 1.1. Теория Призма - это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани - параллелограммами. Грани, которые находятся в параллельных плоскостях, называются основаниями призмы, а остальные грани - боковыми гранями призмы. В зависимости от основания призмы бывают треугольными (рис. 1), четырёхугольными (рис. 2 и 3), шестиугольными (рис. 4) и др.
Призма с боковыми рёбрами, перпендикулярными её основаниям, называется прямой призмой (рис. 1 - 4).
Расстояние между основаниями призмы называется высотой призмы. Высота прямой призмы совпадает с боковым ребром. Высота наклонной призмы видна на рис. 5. Без дополнительных условий невозможно определить, в какую точке проектируется высота наклонной призмы. Прямая призма называется правильной, если её основания - правильные многоугольники. Параллелепипед - это четырёхугольная призма, все грани которой являются параллелограммами. Параллелепипеды - особая группа призм. Как видно на данных рисунках, объёмные рисунки прямых параллелепипедов практически не отличаются. Виды параллелепипедов
Виды прямых параллелепипедов
Специальные случаи прямоугольного параллелепипеда
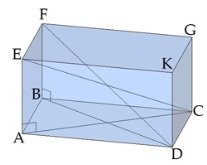
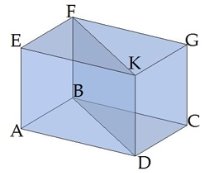
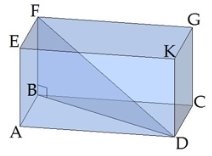
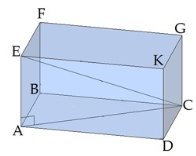
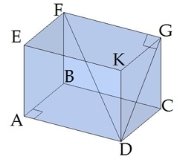
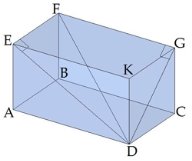
Диагональ призмы - это отрезок, который соединяет две вершины, не принадлежащие одной грани. Диагональ не существует только у треугольной призмы.
Если диагонали основания прямой призмы равны, то диагонали самой призмы тоже равны. Например, у куба, правильной четырёхугольной призмы, прямоугольного параллелепипеда диагонали равны (DF = EC, т.к. DB = CA), а у параллелепипеда, в основании которого находится параллелограмм, диагонали только попарно равны (DF≠EC, т.к. DB≠CA).
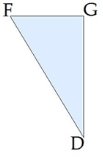
Диагональное сечение призмы - это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани. Каждое диагональное сечение содержит две диагонали призмы.
Диагональное сечение прямой призмы является прямоугольником.
Диагональное сечение наклонной призмы - параллелограмм.
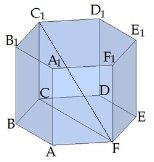
Запомните! У правильного шестиугольника диагонали бывают 2 видов - короткие и длинные. В связи с этим существует два вида диагональных сечений шестиугольной призмы:
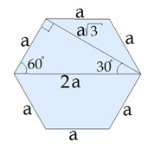
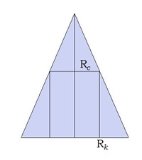
Как найти диагонали правильного шестиугольника, если известна длина его стороны. СЕ - одна из коротких диагоналей шестиугольника, ВЕ - одна из длинных диагоналей. Учитывая то, что углы правильного шестиугольника равны по 120 градусов, легко найти прямоугольный треугольник, в котором есть угол 30 градусов, и использовать соотношения в этом треугольнике.
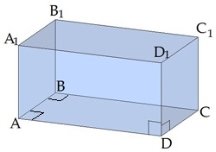
Прямая призма, основанием которой является прямоугольник, называется прямоугольным параллелепипедом. Длины трех ребер, имеющих общую вершину, называются измерениями прямоугольного параллелепипеда.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений:
На рисунке: DB12=DA2+DC2+DD12
Запомните: у прямоугольного параллелепипеда все диагонали равны: DB1=CA1=AC1=BD1
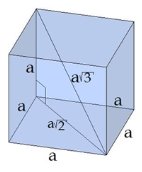
Формула диагоналей куба
При решении задач очень важно уметь обозначать углы, образованные диагоналями призмы и её боковыми гранями.
Угол между наклонной и плоскостью - это угол между наклонной и её проекцией на эту плоскость.
Чтобы найти угол между наклонной и плоскостью, необходимо: 2) из конца наклонной провести перпендикуляр к плоскости; 3) провести проекцию наклонной; 4) обозначить угол между наклонной и её проекцией. Угол между диагональю и плоскостью основания в прямом параллелепипеде
Угол между диагональю и боковой гранью прямоугольного параллелепипеда
Угол, образованный диагональю и плоскостью основания правильной шестиугольной призмы
Площадью боковой поверхности призмы называется сумма площадей всех боковых граней призмы. Площадь боковой поверхности прямой призмы Sбок.=Pосн.⋅H, где H - высота призмы.
Площадь полной поверхности призмы - сумма площадей всех граней призмы. Она состоит из площади боковой поверхности и площади оснований Sполн.=Sбок.+2⋅Sосн.
Все грани куба - квадраты, поэтому рациональнее использовать формулу Sполн. пов. куба=6⋅ a 2
Обьём прямой призмы находится по формуле: V=Sосн.⋅H
Для прямоугольного параллелепипеда можно использовать формулу V=abc , где a, b, c - измерения прямоугольного параллелепипеда (длина, ширина, высота).
Для куба используется формула V=a3, где a - ребро куба.
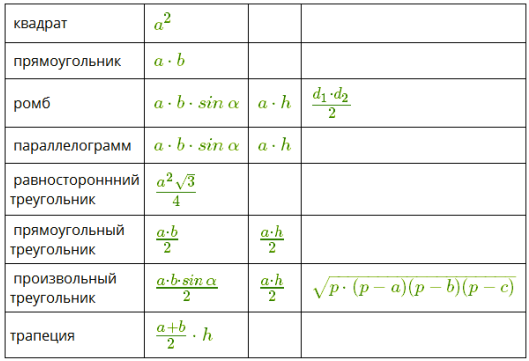
Основанием призмы может быть любой n-угольник, поэтому важно знать формулы вычисления их площадей.
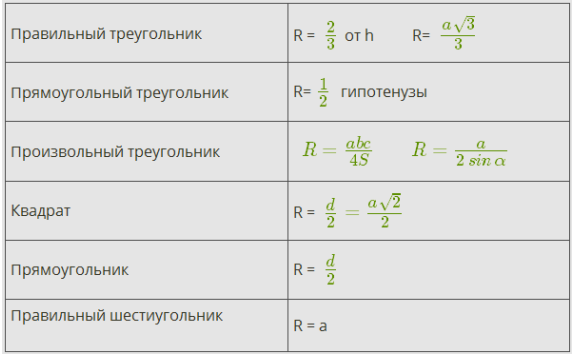
Важные формулы нахождения площади n-угольников
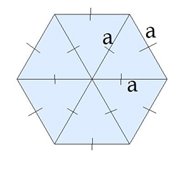
Формула нахождения площади правильного шестиугольника
1.2. Онлайн -ресурсы
http://ua.onlinemschool.com/math/assistance/figures_area_1/cube/ http://ua.onlinemschool.com/math/assistance/figures_volume/prism/
http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/obem-pryamougolnogo-parallelepipeda http://ua.onlinemschool.com/math/assistance/figures_volume/cube/ http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/obem- pryamougolnogo-parallelepipeda http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/obem-pryamoj-prizmy http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/obem-naklonnoj-prizmy http://www.youtube.com/watch?v=LR5jg1q3kPo http://free.megacampus.ru/xbookM0001/index.html?go=part-069*page.htm
1.3. Урок
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Тема: « Понятие объема. Объем прямоугольного параллелепипеда» Цель урока: Ввести понятие объема тела, рассмотреть свойства объемов, теорему об объеме прямоугольного параллелепипеда и следствие об объеме прямой призмы, основанием которой является прямоугольный треугольник; сформировать умение применять данный материал при решении задач. ХОД УРОКА
Сообщение темы и целей урока, актуальность данной темы
Что называется параллелепипедом? прямоугольным параллелепипедом? Какие свойства прямоугольного параллелепипеда вы знаете? III. Объяснение нового материала 1) Понятие объема тела Еще в глубокой древности у людей возникла необходимость в измерении количества различных веществ. Сыпучие вещества и жидкости можно было мерить, наполняя ими сосуды определенной вместимости, т.е. определяя их количество по объему. Понятие объема в стереометрии вводится аналогично понятию площади в планиметрии. В планиметрии мы определяли площадь так: площадь многоугольника – это величина той части плоскости, которую занимает многоугольник. Сформулировать аналогично данному понятию понятие объема. Величина части пространства, занимаемого геометрическим телом, называется объемом этого тела. 2) Единицы измерения объема
В повседневной жизни нам часто приходится определять объемы различных тел. Например, коробки, банки. В житейской практике единицами объема служили меры емкости, используемые для хранения сыпучих и жидких тел.
В Киевской Руси существовала мера зерна – кадь. ( Это примерно 230 кг ржи) Жидкости же мерили бочками и ведрами. В XIX в. система мер жидкости имела вид:
Для того, чтобы определить какая из двух емкостей вместительнее, можно заполнить одну из них водой, а затем проверить, вся ли вода поместится в другую, и если вся, то заполнит ли она ее полностью. Однако решить эту задачу иначе – вычислить объем каждой емкости. Для этого нам нужны единицы объемов. Когда в планиметрии мы вводили единицы площади, то за единицу площади брали квадрат со стороной 1 см (1 см2). Аналогично, за 1см3 принимаем куб с ребром 1 см. Процедура измерения объемов аналогична процедуре измерения площадей. Число измерения (единичных кубов) и частей единицы, содержащихся в данном теле, принимается за числовое значение объема при выбранной единице измерения. Это число может быть как рациональным (в частности, целым), так и иррациональным. 3) Свойства объемов Аналогичны свойствам площадей в планиметрии.
4) Объем прямоугольного параллелепипеда
Поиск формул, позволяющих вычислять объемы различных тел, был долог. Мы будем находить объем прямоугольного параллелепипеда, используя следующую теорему ( давно знакомая вам формула, попробуйте сформулировать эту теорему): Теорема: Объем прямоугольного параллелепипеда равен произведению трех его измерений. V = abc 5) Следствия Рассмотрим следствия из данной теоремы 1. Объем прямоугольного параллелепипеда, равен произведению площади основания на высоту. 2. Объем прямой призмы, основанием которой является прямоугольный треугольник, равен произведению площади основания на высоту. IV. Закрепление
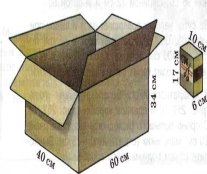
Задача 1 Сколько пакетов с соком войдет в коробку?
Найдите объем тела:
Задача 3
Задача 4 За сутки человек совершает вдох и выдох примерно 23 000 раз. За один вдох в легкие поступает 500 см3 воздуха. Какой объем воздуха ( в литрах) проходит через легкие человека за сутки? Задача 5 Больному прописали глазные капли, по 2 капли 3 раза в день в оба глаза. Во флаконе 10 мл лекарства. Объем капли 1/9 мл. Хватит ли одного флакона на неделю? № 1. Измерения прямоугольного параллелепипеда равны 8 см, 12 см и 18 см. Найдите ребро куба, объем которого равен объему этого параллелепипеда. Учащиеся решают данную задачу на листочках, затем в рабочую тетрадь записывают только ответ, а листок с решением сдают учителю. После этого решение с ответом отображается на экране, учащиеся проверяют свое решение и ответ. № 2. Диагональ прямоугольного параллелепипеда равна 18 см и составляет угол в 30° с плоскостью боковой грани и угол в 45°с боковым ребром. Найдите объем прямоугольного параллелепипеда. Учащиеся на местах обдумывают решение, затем один выходит к доске и демонстрирует решение. V. Итог урока Что такое объем тела? Какие единицы измерения вы знаете? Какие свойства объема вы знаете? Сформулируйте теорему о объеме прямоугольного параллелепипеда и следствия из нее. VI. Домашнее задание п. №
1.4. Тест Тест по теме: « Призма» Вариант №1 Уровень A |
|||||||||||||||||||||||||||||||||||||||||||
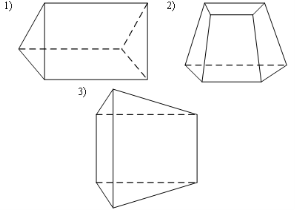 1. Призма изображена на рисунке…
1. Призма изображена на рисунке…
2. 6 – это число…
1) вершин шестиугольной призмы;
2) рёбер треугольной призмы;
3) граней четырёхугольной призмы.
3. Не существует призмы, у которой все грани…
1) ромбы;
2) прямоугольники;
3) треугольники.
4. Существует призма, которая имеет…
1) 13 рёбер; 2) 14 рёбер; 3) 15 рёбер.
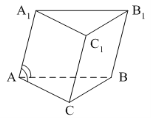 5. ABCA1B1C1 – наклонная призма.
5. ABCA1B1C1 – наклонная призма. ![]()
Тогда СС1B1B не может быть…
1) ромбом;
2) квадратом;
3) прямоугольником.
6. ABCDA1B1C1D1 – прямой параллелепипед. ![]() – угол между диагональю DB1 и плоскостью DD1C1.
– угол между диагональю DB1 и плоскостью DD1C1.
Тогда ABCD –
1) ромб;
2) квадрат;
3) прямоугольник.
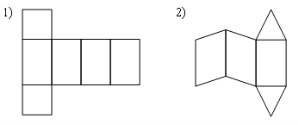
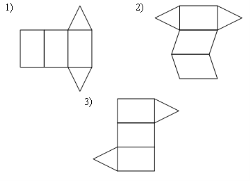
7. Развёрткой наклонной призмы является фигура под номером…
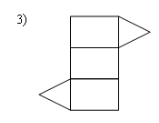
Уровень B
1. В правильной четырёхугольной призме площадь основания равна 144 см2, а высота равна 14 см. Тогда длина диагонали этой призмы…
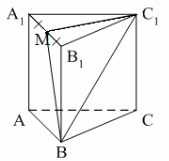
2. ABCA1B1C1 – правильная призма. A1M = MB1.
Тогда ![]() …
…
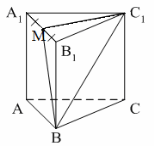
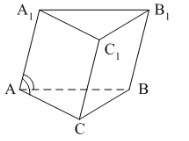
3. ABCA1B1C1 – прямая призма, АА1 = 6 см. АС = 12 см, ![]()
Тогда тангенс угла между плоскостями АВС и А1ВС равен…
Вариант №2
Уровень А
1. Призма изображена на рисунке…
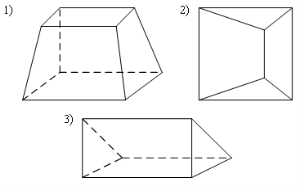
2. 9 – это число…
1) вершин девятиугольной призмы;
2) рёбер треугольной призмы;
3) граней четырёхугольной призмы.
3. Не существует призмы, у которой все грани…
1) ромбы;
 2) квадраты;
2) квадраты;
3) трапеции.
4. Число рёбер призмы кратно… 1) 5; 2) 2; 3) 3
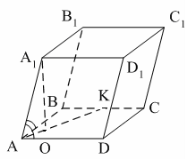
5. ABCDA1B1C1D1 – наклонный параллелепипед. ![]()
![]()
![]() биссектрисе AK. Тогда ABCD…
биссектрисе AK. Тогда ABCD…
1) прямоугольник;
2) ромб:
3) квадрат.
 6. ABCA1B1C1 – правильная призма. Тогда угол между BC1 и плоскостью АВВ1 – это…
6. ABCA1B1C1 – правильная призма. Тогда угол между BC1 и плоскостью АВВ1 – это…
1) ![]()
2) ![]()
3) ![]()
7. Не является развёрткой правильной призмы фигура под номером…
Уровень В
 1. Диагональ основания правильной четырёхугольной призмы равна 8 см, а диагональ боковой грани – 7 см. Тогда диагональ призмы равна…
1. Диагональ основания правильной четырёхугольной призмы равна 8 см, а диагональ боковой грани – 7 см. Тогда диагональ призмы равна…
2. Все рёбра наклонной треугольной призмы равны по 4 см. Боковое ребро АА1 составляет с рёбрами оснований углы по 30°.
Тогда площадь боковой поверхности равна…
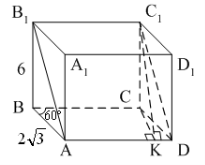
3. ABCDA1B1C1D1 – прямая призма, АА1 = 6 см. ABCD – параллелограмм, ![]() см,
см, ![]()
Тогда тангенс угла между плоскостями АВС и АВ1С1 равен…
Ключ к тесту по теме: « Призма»
|
№ п/п вариант |
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
А7 |
В1 |
В2 |
В3 |
|
1 |
1 |
3 |
3 |
3 |
1 |
1 |
2 |
22 |
90° |
4 |
|
2 |
3 |
2 |
3 |
3 |
1 |
2 |
2 |
9 |
32 |
2 |
|
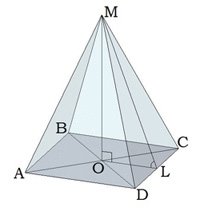
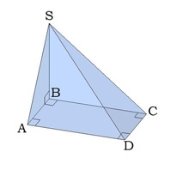
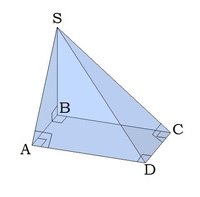
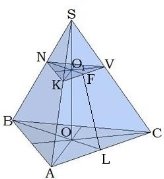
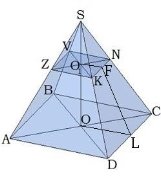
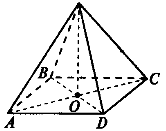
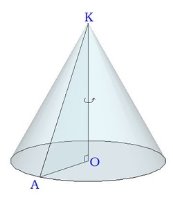
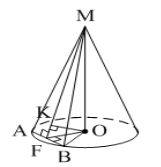
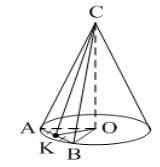
Тема 2 Пирамида Цель: Сформировать представление о пирамиде и ее элементы, нахождение площадей боковой и полной поверхностей пирамиды, формировать умения и навыки учащихся решать задачи на использование пирамид. 2.1. Теория Многогранник, одна грань которого является n-угольником, а остальные грани - треугольники с общей вершиной, называется пирамидой, n-угольник называется основанием пирамиды, а треугольники - боковыми гранями. Общая вершина боковых граней называется вершиной пирамиды. Отрезки, соединяющие вершину пирамиды с вершинами основания, называются рёбрами пирамиды.
В зависимости от количества сторон основания, пирамиды могут быть треугольными, четырёхугольными, пятиугольными и т. д.
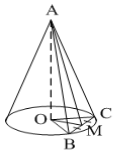
Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды. Важно знать, где на плоскости основания находится проекция вершины пирамиды, она может быть в центре основания, на стороне основания, за пределами многоугольника основания. Решение задачи в большей степени зависит от расположения этой точки.
Чтобы нарисовать пирамиду, нужно соблюдать определённый порядок: 1) первым рисуется основание, 2) по условию задачи находится проекция вершины на плоскости основания, 3) вертикально проводится высота, 4) проводятся рёбра.
В курсе школы в основном есть задачи, в которых даны:
Углы пирамиды
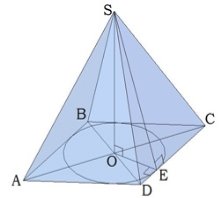
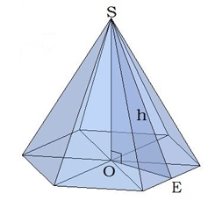
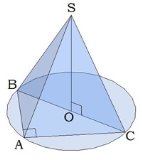
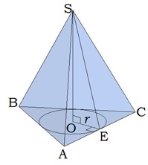
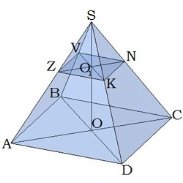
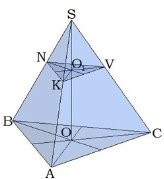
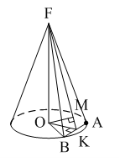
Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды. Запомните: двугранный угол образуется двумя перпендикулярами. На рис. ∢OES. Чтобы определить этот угол, часто нужно использовать теорему о трёх перпендикулярах. Углы, которые образованы боковым ребром и его проекцией на плоскость основания, называются углами между боковым ребром и плоскостью основания. На рис.∢OCS.
Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды.
Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды. На рис.∢DSC.
Основаые формулы пирамиды
Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды: S=S1+S2+S3+...
Некоторые формулы годятся только для определённых видов пирамиды.
Площадь полной поверхности Sп.п.=S+Sоснования
Объём пирамиды V = 1/3Sоснования*H, где H - высота пирамиды.
Формула объёма используется для пирамид любого вида. Пирамида, основанием которой явялется правильный многоугольник, и вершина пирамиды проектируется в центр основания, называется правильной пирамидой. Боковые грани правильной пирамиды - равные равнобедренные треугольники. Высота боковой грани правильной пирамиды называется апофемой. Правильная треугольная пирамида, у которой все рёбра равны, называется тетраэдром. Все грани тетраэдра - равные равносторонние треугольники.
В школе нужно уметь решать задачи, где дана -правильная треугольная пирамида (рис. 1) -правильная четырёхугольная пирамида (рис. 2) -правильная шестиугольная пирамида (рис.3)
Формулы Для вычисления площади боковой поверхности правильной пирамиды существуют две формулы:
, где P - периметр основания, h - апофема, ϕ - двугранный угол при основании.
Объём пирамиды V =
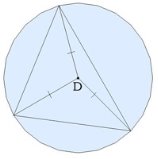
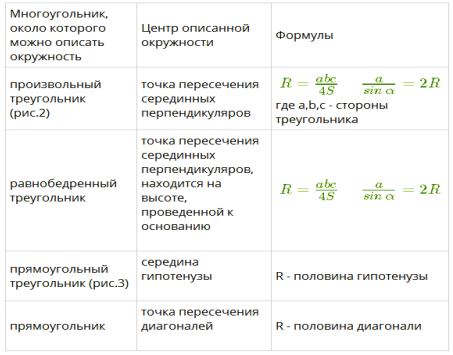
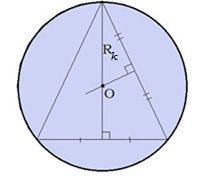
Не путайте h - апофему с H - высотой пирамиды! Если боковые рёбра пирамиды с плоскостью основания образуют равные углы, то рёбра пирамиды равны, и вершина пирамиды проектируется в центр окружности, описанной около многоугольника основания.
У пирамиды могут быть равны боковые рёбра тогда, когда около многоугольника основания можно описать окружность.
Рис. 2 Рис. 3 Главные зависимости для многоугольников, около которых можно описать окружность
Для таких пирамид нельзя использовать формулы правильной пирамиды для вычисления площади боковой поверхности, площадь боковой поверхности находят, сложив площади всех боковых граней пирамиды. Ss=S1+S2+...
Если основание - правильный многоугольник и все боковые грани равны, то пирамида является правильной.
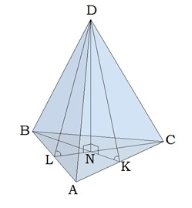
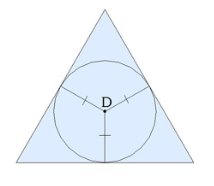
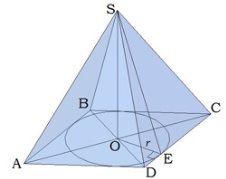
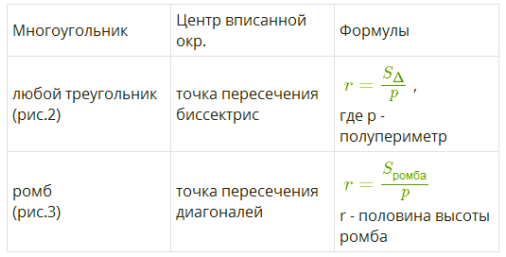
Если боковые грани пирамиды с её основанием образуют равные двугранные углы, то все высоты боковых граней пирамиды равны (у правильной пирамиды это апофемы), и вершина пирамиды проектируется в центр окружности, вписанной в многоугольник основания.
Для таких пирамид при вычислении площади боковой поверхности применяются формулы, которые используются для правильной пирамиды.
У пирамиды могут быть равные двугранные углы при основании тогда, когда в многоугольник основания можно вписать окружность.
Рис. 2 Рис. 3
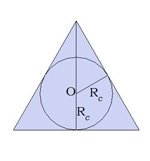
Отмечая радиус r на рисунке, нужно быть очень внимательным! Радиус вписанной окружности перпендикулярен стороне. Главные зависимости для многоугольников, в которые можно вписать окружность
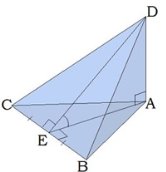
Если у пирамиды одно ребро перпендикулярно плоскости основания, то вершина пирамиды проектируется в одну из вершин основания. На первом рисунке дана треугольная пирамида с одной гранью, перпендикулярной основанию.
На втором рисунке дана пирамида, основание которой - прямоугольник.
ТТП - прямая, которая проведена на плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.
Записываем с помощью символов:
У таких пирамид площадь боковой поверхности равна сумме площадей всех боковых граней Ss=S1+S2+... (нельзя использовать формулу правильной пирамиды).
Формула нахождения обьёма применяется для всех видов пирамид:
Обьём усечённой пирамиды
h - апофема правильной усечённой пирамиды, на данных рисунках это отрезок LF.
2.2. Онлайн -ресурсы http://ua.onlinemschool.com/math/assistance/figures_volume/pyramid/ http://ua.onlinemschool.com/math/assistance/figures_volume/tetrahedron/ http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/ob-em-piramidy http://rutube.ru/video/00f11d6d2b10df0a02404de488025d8b/?ref=relroll https://www.youtube.com/watch?v=J7dHXVSeeBk http://free.megacampus.ru/xbookM0001/index.html?go=part-069*page.htm |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
2.3. Урок
Задачи: Обучающая:Изучение понятия «объем пирамиды» и практическое применение; полученных знаний при решении прикладных задач; умение проводить параллель между экономическими и математическими понятиями. Развивающая: развитие творческого отношения обучающихся к применению теоретических знаний к прикладным вопросам математики и экономики; развитие и формирование у обучающихся информационной и коммуникационной компетенции; развитие внимания, памяти, речи, логического мышления при решении задач, умения анализировать. Воспитательная: воспитание и развитие коммуникационных способностей: работа в группе, в паре; воспитание научного отношения к решению жизненных проблем; воспитание самостоятельности, самоконтроля, самооценки.
Тип урока: бинарный. Межпредметные связи: математика, экономика. Оборудование к уроку:
Предлагаемые медиоматериалы:
http://video.mail.ru/mail/soltanovskaja/135/24.html http://www.videoinet.ru/view.html?id=1X07saF09qw2bUZ Ход урока
На прошлых занятиях мы рассмотрели одно из Платоновых тел многогранник – пирамида. Мы изучили основные элементы пирамиды, её свойства. Научились вычислять высоту, площадь основания, площадь полной и боковой поверхности пирамиды, объём. Сегодня мы с вами ещё раз обратимся к такому понятию как объём пирамиды. Научимся решать задачи с элементами экономики, исследуем экономическую и математическую связь в вычислении объёма пирамид, то есть пополним знания по предмету «математика» и «экономика». Предлагаю вам ответить на следующие вопросы (фронтальный опрос):
Учитель: Давайте еще раз обратимся к истории создания пирамид и послушаем сообщение вашего товарища (задание для сообщения выдается заранее). Ученики: Первые сооружения, имеющие форму пирамиды, были воздвигнуты более 5 тыс. лет назад в Египте из известняка по строго математическим расчётам. Данное сооружение и по сей день вызывает восхищение, и входило в известные «семь чудес света». Предлагаю вашему вниманию видеофильм о Египетских пирамидах. (Видео ролик о Египетских пирамидах: http://video.mail.ru/mail/soltanovskaja/135/24.html ) Учитель: Сегодня на уроке мы постараемся исследовать математическую и экономическую зависимость в вычислении объёма пирамиды через решение прикладных задач. Впервые формулу объёма пирамиды вывел известный древнегреческий учёный из города Сиракуз - Архимед.
Почему Архимед применил данное название именно к этой модели многогранников. Это понятие мы можем разобрать с экономической точки зрения. Учитель экономики: «Чертовой лестница» - это не что иное, как прототип лестницы ведущей к образованию финансовой пирамиды. Из курса геометрии вы знаете, что основанием математической пирамиды называют её нижнюю грань. То есть тело в форме пирамиды устойчиво стоит на горизонтальной поверхности. Для создания финансовой пирамиды необходимо сформировать ее основание (используется минимальное число боковых граней пирамиды - три). То есть для построение организации на основе финансовой пирамиды достаточно всего три человека, Итак, значит первая ступень создания финансовой пирамиды – то есть её основания - это привлечение капитала как минимум трех человек. Эти организаторы начинают своё движение вверх по ступенькам «чертовой лестницы», в целях привлечения клиентов и сбора финансовых средств. За незначительное время капитал фирмы (т.е. высота пирамиды) возрастает в десятки раз, при этом объём пирамиды (т.е. финансы организации) увеличивается в сотни раз. Но в один прекрасный момент наращивание капитала прекращается, а значит цель организатора финансовой пирамиды, достигнута (все грани фирмы соединяются в верхней части пирамиды – вершине). Пирамида начинает переворачиваться, иначе - становится с ног на голову и Верхушка пирамиды финансируется за счет расширения основания и привлечения новых участников. Как только основа перестает расширяться, а это неизбежно происходит, то пирамида рушится. При этом те, кто пришел в фирму, построенную по принципу финансовой пирамиды последним, и не является её руководителем, теряют все. Наступает финансовый крах. Предлагаем вашему вниманию небольшой видеоролик о том, как работает финансовая пирамида: http://www.videoinet.ru/view.html?id=1X07saF09qw2bUZ.
Учитель: А теперь перейдем к решению прикладных задач. (В начале урока группа поделена на 2 подгруппы (круглые столы). Обучающимся выдается раздаточный материал, который содержит по 2 задачи, которые надо решить и сделать экономический вывод по полученным результатам (Приложение к уроку № 2, № 3). (У доски решают задачи 4 человека). Задачи 1 подгруппы (с решением):
Учитель: По результатам исследования (решение задач) какой вывод сделает команда 1 подгруппы? Ученики 1 подгруппы должны сделать следующий вывод: чем больше высота пирамиды, тем больше её объём. Следовательно, чем больше клиентов будет привлечено в финансовую компанию, тем больший капитал получат от действия организаторы фирмы, работающие по действию финансовой пирамиды. Задачи 2 подгруппы (с решением):
Ученики 2 подгруппы должны сделать следующий вывод: чем больше площадь основания пирамиды тем больше и итоговый объем пирамиды. Следовательно, чем больше первоначального капитал организаторов фирмы по типу финансовой пирамиды, тем быстрее и итоговый капитал фирмы на момент краха. Преподаватель предлагает обучающимся сделать общий экономический вывод по решению разного вида экономических задач. Обучающие должны сделать следующие выводы:
Вывод по уроку: сегодня, мы закрепили знания по математике и экономике пользуя понятием «объема пирамиды», исследовали зависимость математического и экономического понятия, научились применять теоретические знания по математике к прикладным вопросам экономики.
2.4. Тест Вариант-1
а) все ребра правильной пирамиды равны;
а) 9 см2 б)10 см2 в)12 см2 г) другой ответ.
а) 6см, б)
а) 3
а) прямоугольный б) остроугольный в) тупоугольный г) недостаточно данных.
а) все грани правильной пирамиды равны;
а) 9 см2 б)10 см2 в)12 см2 г) другой ответ.
а) 2
а) 14
а) прямоугольный
Тема 3. Цилиндр Цели: введение понятия цилиндрической поверхности, цилиндра и его элементов; рассмотрение различных видов сечения цилиндра плоскостью; выведение формул для вычисления площадей боковой и полной поверхностей цилиндра;развитие пространственного мышления.
Цилиндр - тело вращения, которое получается при вращении прямоугольника вокруг его стороны.
Полученная цилиндрическая плоскость называется боковой поверхностью цилиндра, а круги - основаниями цилиндра. Осевое сечение цилиндра - это сечение цилиндра плоскостью, которая проходит через ось цилиндра.
При сечении цилиндра плоскостью, параллельной оси цилиндра (т.е. перпендикулярной основанию), получается прямоугольник.
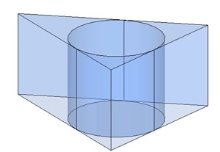
Геометрические тела можно расположить одно в другом. Например, призму можно вписать в цилиндр.
На первом рисунке призма нарисована внутри цилиндра, но это не означает, что она вписана в цилиндр. На втором рисунке выполняются все условия для того, чтобы призма была вписанной в цилиндр.
рис. 1 рис. 2
Чтобы решать задачи, в которых даны комбинации геометрических тел, нужно уметь: 1) описать взаимное расположение тел (знать определения); 2) указать общие точки или элементы; 3) если дан шар, то показать местонахождение его центра; 4) обосновать возможность вписания или описания данного тела; 5) отобразить данную комбинацию тел наиболее удобным способом; 6) сделать выводы о взаимосвязях величин.
В курсе средней школы нужно знать:
комбинации шара с кубом, цилиндром и конусом; взаимные комбинации цилиндра и призмы; взаимные комбинации конуса и пирамиды; взаимные комбинации конуса и цилиндра. Каждую из комбинаций можно выразить двумя способами. Шар, описанный около куба - тоже самое, что и куб, вписанный в шар. Призма, вписанная в пирамиду - то же самое, что и пирамида, описанная около призмы. При решении задач редко рисуется объёмный рисунок комбинации тел, чаще используются рисунки оснований или сечений. Призмой, вписанной в цилиндр, называется такая призма, многоугольники оснований которой вписаны в окружности оснований цилиндра, а боковыми ребрами являются образующие цилиндра.
Цилиндр можно описать только около такой прямой призмы, около основания которой можно описать окружность. Например, цилиндр можно описать около прямой треугольной призмы (см. рис. 1), около правильной призмы, в основании которой находится квадрат (рис. 2).
Рисунок составляется в зависимости от содержания задания, часто достаточно рисунка основания комбинаций этих тел, т.к. высота призмы равна высоте цилиндра.
рис. 3 рис. 4
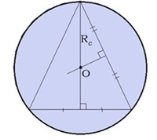
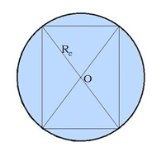
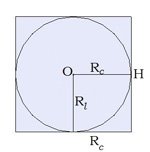
Центр окружности, описанной около треугольника, является точкой пересечения серединных перпендикуляров к сторонам треугольника (см. рис. 3), центр окружности, описанной около квадрата является точкой пересечения диагоналей квадрата (см. рис.4). Радиус цилиндра - это радиус окружности, описанной около многоугольника основания призмы.
Формулы вычисления радиуса R описанной окружности:
где a,b,c стороны, h - высота, d - диагональ.
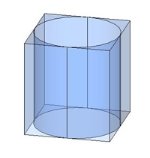
Теория 6. Призма, описанная около цилиндра Призмой, описанной около цилиндра, называется призма, многоугольники оснований которой описаны около окружностей основания цилиндра, а боковые грани касаются цилиндра.
рис. 1
рис. 2
Например, цилиндр можно вписать в прямую треугольную призму (см. рис.1); в правильную призму; в прямую призму, основанием которой является ромб (см. рис. 2).
Рисунок создаётся в зависимости от содержания задачи, часто достаточно нарисовать основание комбинации этих тел, т.к. высота цилиндра равна высоте призмы.
рис. 3 рис. 4
Центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника (см. рис.3), центр окружности, вписанной в квадрат, является точкой пересечения диагоналей квадрата (см. рис. 4).
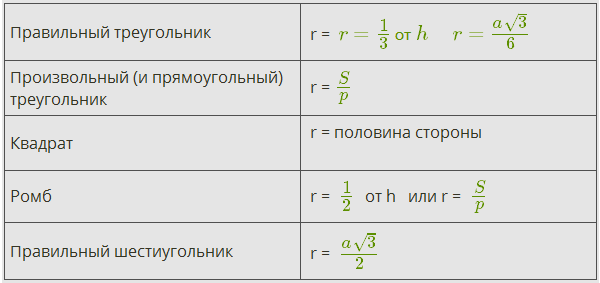
Радиус цилиндра - радиус окружности, вписанной в многоугольник основания призмы.
Формулы вычисления радиуса r вписанной окружности:
где h - высота, S - площадь, p- полупериметр, a - сторона.
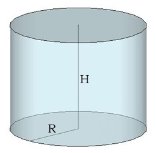
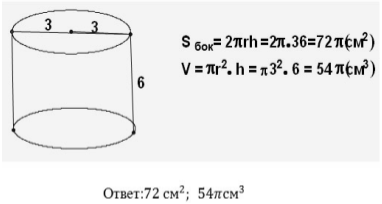
Основания цилиндра - круги. S(круга) = πR2.
Площадь полной поверхности цилиндра равна: S(полн.) = 2S(осн.) + S(бок.) = 2πR2 + 2πRH
Объём цилиндра V(цилиндра) = πR2⋅H. 3.2. Онлайн -ресурсы http://ua.onlinemschool.com/math/assistance/figures_area_1/cylinder/ http://ua.onlinemschool.com/math/assistance/figures_volume/cylinder/ http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/ob-em-tsilindra https://www.youtube.com/watch?v=nOIvkNMEy_4 http://free.megacampus.ru/xbookM0001/index.html?go=part-069*page.htm
3.3. Урок Тема: "Тела вращения. Цилиндр" Цели урока:
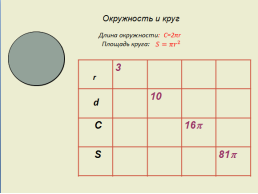
Метод обучения: объяснительно-иллюстративный. Формы обучения: фронтальная, групповая, индивидуадьная. Тип урока: комбинированный урок. Оборудование: маркерная доска, компьютер, мультимедиа-проектор, модель цилиндра. Ход урока 1. Повторение Окружность и круг С понятиями окружность и круг вы уже знакомы. Вспомните, какие известные вам предметы имеют форму окружности (слайд №2). Основные понятия, связанные с окружностью - радиус, диаметр, хорда (демонстрируются на слайде). А теперь – примеры предметов, имеющих форму круга (на слайде). Вспоминаем формулы для нахождения длины окружности и площади круга (на слайде). Заполнение предложенной таблицы позволит вспомнить перечисленные понятия и формулы (на слайде).
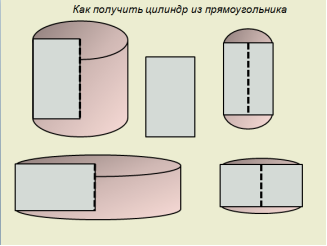
2. Основная часть Как получить цилиндр из прямоугольника Тела вращения – это геометрические тела, полученные при вращении плоских многоугольников вокруг оси. Возьмём, к примеру, прямоугольник (слайд №3). Если вращать его вокруг одной из сторон, получим тело вращения цилиндр.
Как вы думаете, сколько разных цилиндров можно получить, вращая один и тот же прямоугольник? Вокруг большей стороны (на слайде); Вокруг меньшей стороны (на слайде); Вокруг оси симметрии, параллельной большей стороне (на слайде); Вокруг оси симметрии, параллельной меньшей стороне (на слайде). Основные элементы цилиндра Введём определения основных элементов цилиндра и рассмотрим их на чертеже (слайд №4):
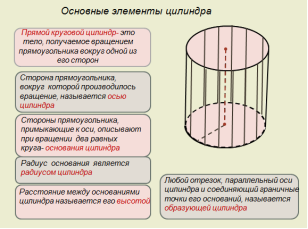
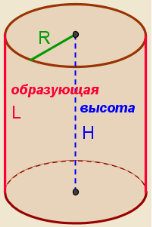
Прямой круговой цилиндр – это тело, получаемое вращением прямоугольника вокруг одной из его сторон (на слайде). Сторона прямоугольника, вокруг производилось вращение, называется осью цилиндра (на слайде). Стороны прямоугольника, примыкающие к оси, описывают при вращении два равных круга- основания цилиндра (на слайде). Радиус основания является радиусом цилиндра (на слайде). Расстояние между основаниями цилиндра называется его высотой (на слайде). Любой отрезок, параллельный оси цилиндра и соединяющий граничные точки его оснований, называется образующей цилиндра (на слайде). Сечения цилиндра плоскостью Рассмотрим, какие фигуры получаются при пересечении цилиндра плоскостью (слайд №5):
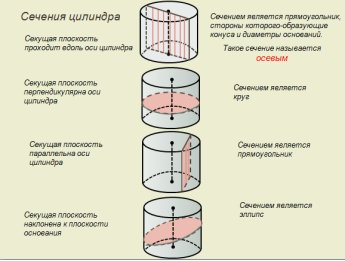
Секущая плоскость проходит вдоль оси цилиндра. Сечением является прямоугольник, стороны которого - образующие конуса и диаметры оснований. Такое сечение называется осевым (на слайде). Секущая плоскость перпендикулярна оси цилиндра. Сечением является круг (на слайде). Секущая плоскость параллельна оси цилиндра. Сечением является прямоугольник (на слайде). Секущая плоскость наклонена к плоскости основания. Сечением является эллипс или его часть (на слайде). 3. Закрепление Письменная работа (слайд №6):
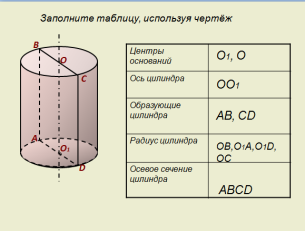
В тетрадях укажите по чертежу основные элементы цилиндра:
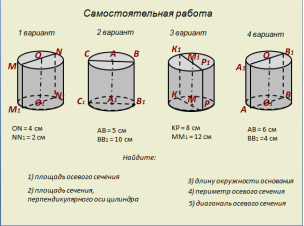
Слайд анимирован, ответы появляются по щелчку мыши во время фронтальной проверки. В следующей работе нужно найти значения основных элементов цилиндра: Самостоятельная работа (слайд №7).
(Работа на 4 варианта с последующей проверкой результатов (слайд №8). Возможный вариант применения: обучающиеся, сидящие рядом или по диагонали, меняются работами с соседями, проверяют работы и сообщают оценку.) Площадь поверхности и объём цилиндра Если разрезать боковую поверхность цилиндра (слайд №9) по образующей, получим прямоугольник (на слайде),одной из сторон которого является длина окружности основания,а другая - высота цилиндра. Применив форулу для нахождения площади прямоугольника, получим:
Для нахождения площади полной поверхности цилиндра прибавим две площади основания (на слайде):
Для нахождения объёма цилиндра площадь основания нужно умножить на высоту:
Решение задач
4. Домашнее задание Проработать конспект. Решить задачи:
3.4. Тест Тест по теме: «Цилиндр» Вариант №1 1. Цилиндр нельзя получить вращением… 1) треугольника вокруг одной из сторон; 2) квадрата вокруг одной из сторон; 3) прямоугольника вокруг одной из сторон.
2. Площадь боковой поверхности цилиндра можно вычислить по формуле…
3. Сечением цилиндра плоскостью, перпендикулярной его образующей, является… 1) круг; 2) прямоугольник; 3) трапеция. 4. На основаниях цилиндра взяты две параллельные друг другу хорды, проходящие через центры оснований. Тогда расстояние между хордами… 1) равно высоте цилиндра; 2) больше высоты цилиндра; 3) меньше высоты цилиндра.
5. Боковой поверхностью цилиндра высотой H и диаметром основания d является квадрат. Тогда верно, что… 1) d = H;
2)
3) 6. Развёрткой боковой поверхности прямого кругового цилиндра может быть… 1) прямоугольник; 2) ромб; 3) параллелограмм.
7. Отношение площадей боковой поверхности и осевого
1)
2)
3)
8. Площадь боковой поверхности цилиндра в 2 раза больше площади основания. Тогда отношение 1) 1; 2) 2; 3) 3.
Вариант №2
1) трапеции вокруг одного из оснований; 2) ромба вокруг одной из диагоналей; 3) прямоугольника вокруг одной из сторон.
2. Площадь боковой поверхности цилиндра нельзя вычислить по формуле…
1)
2)
3)
3. Сечением цилиндра плоскостью, параллельной его образующей, является… 1) круг; 2) прямоугольник; 3) трапеция.
Тогда расстояние между хордами… 1) равно образующей цилиндра; 2) больше высоты цилиндра; 3) меньше образующей цилиндра.
1)
2)
3)
1) прямоугольник; 2) ромб; 3) квадрат.
1) 2) 2 раза;
3)
8. Площадь боковой поверхности цилиндра в 3 раза больше площади основания. Тогда отношение
1) 1; 2) 1,5; 3) 3.
Ключ к тесту по теме: «Цилиндр»
3.5. Практическая работа : Объём цилиндра Цель: закрепить навык решения практических задач на вычисление объёма цилиндра.
Теоретическая часть Прямым круговым цилиндром называется фигура, полученная при вращении прямоугольника вокруг оси содержащей одну из его сторон.
Выполните задания 1 вариант 1 уровень Ответьте на вопросы теста, выбрав один или несколько правильных ответов из предложенных.
а) окружность; б) круг; в) эллипс.
2. Назовите отрезок, который является радиусом: а) О2А1; б) О2О1; в) А4О2.
3. Укажите на рисунке образующую цилиндра: а) О1О2; б) А2А3; в) А1А2.
4. Высота цилиндра это:
а) Расстояние между плоскостями его основания;
5. Какая фигура является осью цилиндра? а) прямая О1О2; б) отрезок О1О2; в) отрезок А1А2.
2 уровень
6. Найдите объем цилиндра с высотой равной 3 см и диаметром основания – 6 см. а)27π см3; б)9π см3 ; в)36π см3; г)18π см3; д)54π см3.
7. Диагональ осевого сечения цилиндра составляет с плоскостью основания цилиндра угол 600. Найдите объем цилиндра, если площадь осевого сечения равна 16
а)16π см3; б)16
8. Площадь осевого сечения цилиндра равна 20 см3, площадь основания - 25π см2. Найдите объем цилиндра.
а) 9π см3; б) 30
9. В основании прямой призмы лежит прямоугольный треугольник с катетами 4 и 1. Боковые ребра равны
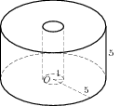
3 уровень 10. Найдите объем V части цилиндра, изображенной на рисунке. 11. В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
1 уровень Ответьте на вопросы теста, выбрав один или несколько правильных ответов из числа предложенных.
1. Какая фигура является осевым сечением цилиндра: а) треугольник; б) круг; в) прямоугольник.
2. Назовите отрезок который является высотой: а) А2А3; б) О2О1; в) А4О2.
3. Укажите на рисунке образующую цилиндра: а) О1О2; б) А2А3; в) А1А2.
а) образующая равна высоте;
5. Объем цилиндра вычисляется по формуле:
а) V = Sосн
2 уровень
6. Найдите объем цилиндра с высотой равной 5 см и диаметром основания – 8 см. а)27π см3; б)9π см3 ; в)36π см3; г) 80π см3; д)54π см3.
7. Диагональ осевого сечения цилиндра составляет с плоскостью основания цилиндра угол 600. Найдите объем цилиндра, если площадь осевого сечения равна
а)16π см3; б) 128
8. Площадь осевого сечения цилиндра равна 12 см3, площадь основания - 16π см2. Найдите объем цилиндра.
а) 24π см3; б)31,5
9. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны
3 уровень 10. Найдите объем V части цилиндра, изображенной на рисунке.
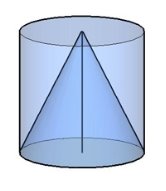
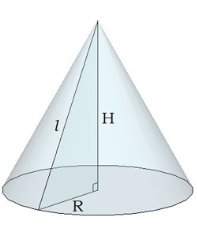
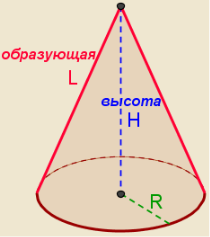
Максимальный балл за работу – 12 балла Тема 4. Конус Цель: Тема «Конус» знакомит школьников с этим геометрическим телом: содержит его определение, понятие об осевом сечении и сечении плоскостью, понятие усеченного конуса, формулы для вычисления площади боковой и полной поверхности конуса, объёма конуса а также боковой поверхности усеченного конуса. 4.1. Теория. Конус - тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.
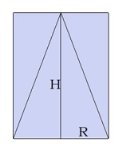
Осевое сечение конуса - это сечение конуса плоскостью, которая проходит через ось конуса.
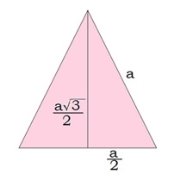
Равносторонним конусом называется конус, осевым сечением которого является равносторонний треугольник.
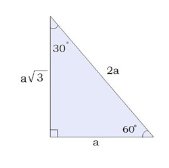
При нахождении элементов равностороннего треугольника, можно использовать соотношения прямоугольного треугольника.
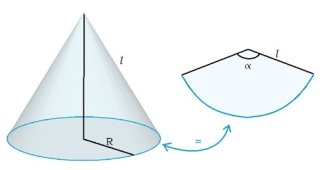
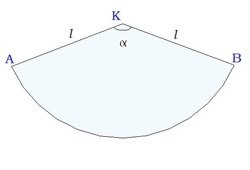
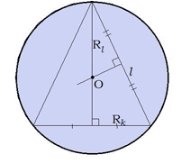
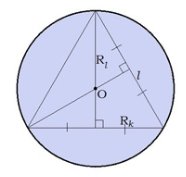
Теория 3 .Выражение радиуса конуса из развёртки боковой поверхности конуса Разверткой боковой поверхности конуса является круговой сектор. Длина дуги сектора - это длина окружности основания конуса.
Длина дуги сектора вычисляется по формуле
Длина окружности основания конуса вычисляется по формуле 2πR, где R - радиус конуса.
Из этого соотношения можно выразить радиус конуса.
В конусе нельзя обозначить угол развёртки.
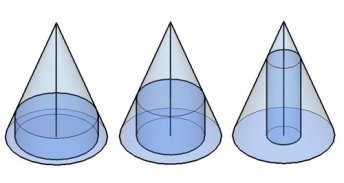
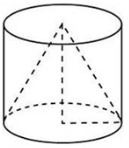
Даны конус и описанный около него цилиндр. Во сколько раз объем цилиндра больше объема конуса? V(цилиндра) = πR2H, а V(конуса) =⅓πR2H, H(цилиндра) = H(конуса) и R(цилиндра) = R(конуса), следовательно, объём любого цилиндра в 3 раза больше объёма вписанного в него конуса. Цилиндр является вписанным в конус, если одно его основание находится в основании конуса, а второе основание касается всех образующих конуса.
В любой конус можно вписать бесконечное множество цилиндров.
Найдите радиусы цилиндра и конуса, если известно, что их отношение равно 1 : 4, а разность равна 6 м. Решение: Радиус конуса обозначаем за x, а радиус цилиндра за y. Составляем систему уравнений:
Ответ: радиус конуса равен 8 м, а радиус цилиндра равен 2 м.
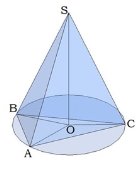
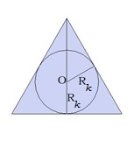
Около конуса можно описать только такую пирамиду, у которой двугранные углы при основании равны. Двугранные углы при основании равны у правильных пирамид и у таких пирамид, высота которых проектируется в центр вписанной окружности.
рис. 2 рис. 3 Окружность основания конуса вписана в многоугольник основания пирамиды.
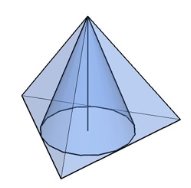
Радиус конуса - радиус окружности, вписанной в многоугольник основания пирамиды. Пирамидой, вписанной в конус, называется такая пирамида, многоугольник основания которой вписан в окружность основания конуса, а вершиной является вершина конуса.
рис. 1 рис. 2
В конус можно вписать только такую пирамиду, боковые рёбра которой равны (совпадают с образующими конуса).
Боковые рёбра равны у любой правильной пирамиды и у таких пирамид, высота которых проектируется в центр описанной окружности.
Рисунки создаются в зависимости от содержания задачи, иногда достаточно изобразить только основания этих тел, т.к. высоты пирамиды и конуса равны.
рис. 3 рис. 4 Окружность основания конуса описана около многоугольника основания пирамиды. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника (см. рис. 3), центром окружности, описанной около четырёхугольника является точка пересечения его диагоналей (см. рис. 4).
Радиус конуса - радиус окружности,описанной около многоугольника основания пирамиды. Площадь поверхности конуса состоит из площади боковой поверхности конуса и площади основания (круга).
Площадью боковой поверхности конуса является площадь ее развёртки. Развёрткой боковой поверхности конуса является круговой сектор.
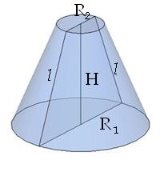
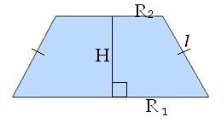
Усечённый конус - тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.
Площадь боковой поверхности усечённого конуса
Sбок.=π⋅l⋅(R1+R2) , где R1и R2 −радиусы оснований, l - образующая.
Объём усечённого конуса
4.2. Онлайн -ресурсы http://ua.onlinemschool.com/math/assistance/figures_area_1/cone/
http://ua.onlinemschool.com/math/assistance/figures_volume/cone/
http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/ob-em- konusa https://www.youtube.com/watch?v=33DXdtJBnjc http://free.megacampus.ru/xbookM0001/index.html?go=part-069*page.htm
4.3. Урок Цели урока:
Тезис урока:
Что без меня предметы?
Ход урока Установление контакта учителя с учениками.
Учитель просит установить связь между этими объектами. “Конус – шишка” (греческий перевод). Идет конструктивный разговор о понятиях и формулах, связанных с конусом.
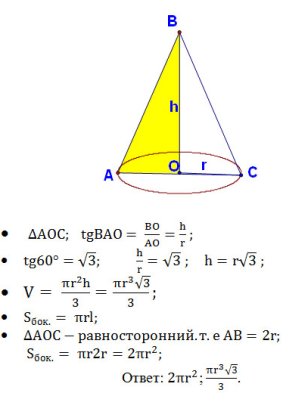
Если вы скажете, что мода такая была, то вы ошибётесь. Ответ прост, они считали, что под колпаком собирается энергия, которая в свою очередь сделает их сильнее и умнее. Водружаем на голову колпак и энергично отправляемся на поиск новой информации о конусе. Первичная актуализация знаний. Решение задач по готовым чертежам . 1. Образующая конуса наклонена к плоскости основания под углом 600. Радиус основания r. Вычислить боковую поверхность конуса и его объем. Решение:
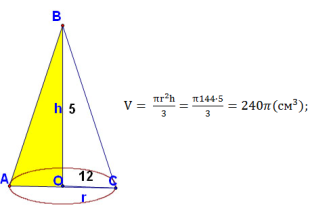
2. В прямоугольном параллелепипеде измерения относятся как 5:3:2. Его объем равен 240 см. Вычислите измерения параллелепипеда. Решение:
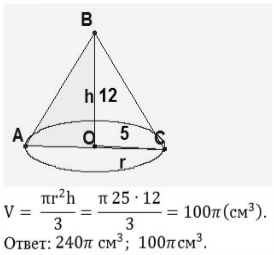
Ответ: 4см; 6см;10см. 3. Прямоугольный треугольник с катетами 5 и 12 см вращается вокруг одного из них. Вычислите объем полученного тела вращения. Решение:
Или
4. Высота равностороннего цилиндра равна 6 см. В равностороннем цилиндре высота равна диаметру основания. Вычислите боковую поверхность цилиндра и его объем. Решение.
Системная актуализация. Защита решения задачи.
Решение математических задач требует от учащихся применения многочисленных мыслительных умений. Они должны анализировать заданную ситуацию; сопоставлять данные и искомые величины; сравнивать решаемую задачу с решенными ранее, выявляя скрытые свойства заданной ситуации; конструировать простейшие математические модели; осуществляя мысленный эксперимент; синтезировать найденные факты, отбирая полезную для решения задачи информацию. Поэтому предлагаю ребятам решение сложных задач готовить заранее в виде групповой защиты своей работы. Группа, защищающая решение задачи, составляется по принципу взаимодополняемости и малоконфликтности. В группе обязательно присутствует сильный лидер, два сильных референта, она работоспособна и управляема. 1. Демонстрируются модели, иллюстрирующие задачу: каркасная, пластилиновая, компьютерный вариант. 2. Предлагается чертеж осевого сечения:
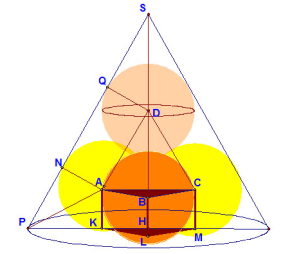
A, B, C – центры шаров, лежащих в основании конуса, D – центр четвертого шара. Основание конуса параллельно плоскости АВС и удалено от нее на расстоянии r. Тетраэдр АВСD – правильный со стороной 2r. Докажем, что высота конуса проходит через точку D и центр треугольника АВС. Высота тетраэдра АВСD проходит через центр АВС. Плоскости основания конуса и плоскость АВС параллельны, т. е. высота конуса и высота тетраэдра параллельны между собой. Пусть K, L, M – проекции точек А, В, С на основание конуса. Ясно, что КLM есть равносторонний треугольник со стороной 2r. В плоскости сечения конуса, проходящей через его высоту SH и точку А, сечением первого шара будет окружность, вписанная в угол SPH. Рассмотрим треугольник АPK, где РА – биссектриса угла SPH . Тогда HK = R – r·ctg (a/2), где R– радиус основания конуса, a – угол SPH. Равносторонний треугольник вписан в окружность, концентрическую с основанием конуса и имеющую радиус R – r·ctg (a/2). Значит, центр треугольника КLM совпадает с центром основания, а, значит, с центром треугольника АВС. Вывод: точка D проектируется в центр основания. Обозначим точки касания сфер с центрами А и D с образующей SP через N и Q.
= a, где G – центр треугольника АВС. DG –высота правильного тетраэдра АВСD, т.е.
Можно ли рассчитать объем конуса при заданных условиях или потребуется дополнительные параметры?
Конус – хищная улитка, притом ядовитая. Охотятся они при помощи зуба – пронзают им жертву, как гарпуном. Питаются морскими червями, моллюсками и небольшими рыбами. С людьми конусы тоже не сюсюкаются. Могут ужалить ничуть не хуже пчелы – и последствия могут быть довольно неприятными. Возможен даже смертельный исход. Но зато медики конусов любят. Их яд считается очень перспективным веществом с медицинской точки зрения. Его тщательно изучают и стремятся ввести в широкое производство. А можно ли использовать эту модель в современной архитектуре?
Проверка аналитического восприятия темы. Расчет комфортности жилища. (Учитель меняет методику закрепления нового материала и предлагает ребятам заняться аналитическим методом восприятия темы “Объемы тел”/) Расчет комфортности жилища определяется по формуле
Намного ли нам комфортнее? Рассчитаем комфортность классной комнаты. Ее размеры: 7м; 3,5м; 12м.
В русском языковом сознании слово “чум” обычно ассоциируется с чукчами, а вообще чумами, чтобы не заморачиваться, зовут все конические шалаши северных жителей. На самом деле, слово это происходит из финно-угорских языков и вовсе не из Сибири. У коми “тсом”, у удмуртов “цум” – это конусовидное лесное или прибрежное хранилище припасов. Так же, к слову, называется мера расстояния – перегон по реке от одного чума до другого. Русские научились этому слову у удмуртов. А когда продвинулись дальше на север и на восток, они увидели, что всякие “дикие сибирские обыватели” в чумах – живут. И саамы, которые лопари, в общем, тоже в них живут, хоть и не сибиряки. Конечно, у всех этих народов жилища назывались, да и выглядели по-разному. Вот, например, кувакса саамов:
Они крыли её мешковиной или брезентом. А это кота. Тоже саамская. Полностью деревянная.
Чум тунгусов-эвенков назывался дю. Тунгусы были пешими кочевниками, Сибирь они освоили третьими – после палеоазиатов и юкагиров. Возможно, именно они и научили все местные племена строить чумы. А может, наоборот, научились у них. Хотя, по-хорошему, конструкция эта настолько проста, что, скорее всего, просто её придумали одновременно разные люди в разных местах. А теперь, собственно, к чукчам. Чукчи живут в ярангах. Вот в таких:
Яранга, конечно, немного похожа на чум, но конструкция у неё сложнее, об этом чуть позже, а сейчас рассчитаем комфортность чума.
= 45,05% Ответ: чум оказался комфортнее классной комнаты. Как показывают типовые расчеты, коэффициент комфортности всегда меньше единицы. Дома вы сможете просчитать комфортность вашего жилья. Существует единственное геометрическое тело, имеющее коэффициент комфортности, равный единице, это шар. Каждый из нас видел неоднократно, как в холодную ночь кот готовится ко сну. Он поджимает под себя лапы и становится шарообразным.
Но это уже другая история, о ней мы состоится разговор на следующем уроке. Наш разговор пойдет о том, что заварной чайник круглой формы остывает медленнее, чем чайник такого же объема, но другой формы.
Домашнее задание. “Читал я где – то, что царь однажды воинам своим велел снести земли по горсти в кучу. И гордый холм возвысился, и царь мог с высоты веселье озирать: И дол, покрытый белыми шатрами, и море, где бежали корабли”. Как вы думаете, кто из наших соотечественников написал эти строки? Как вы думаете, какие формулы нам потребуются для вычисления массы этого холма? Запишите домашнее задание: Рассчитать комфортность вашей комнаты и комфортность проживания в яранге, данные возьмите из интернета. Подготовьтесь к самостоятельной работе .
Тест рассчитан на проверку усвоения учащимися темы урока.
1. Найдите объем V конуса, образующая которого равна 2 и наклонена к плоскости основания под углом 300. В ответе укажите 2. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 3 раза? 3. Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 1,5 раза?
5. Высота конуса равна 6, образующая равна 10. Найдите его объем, деленный на π. 6. Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на π. 7. Конус получается при вращении равнобедренного прямоугольного треугольника АВС вокруг катета, равного 6. Найдите его объем, деленный на π.
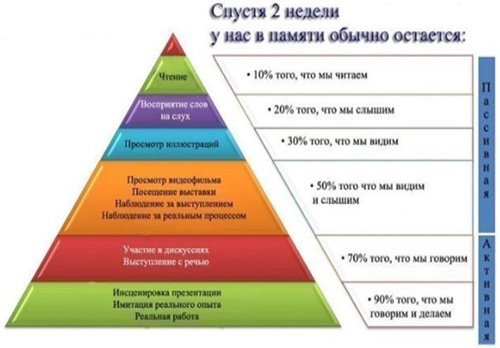
9. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды, больше объема конуса, вписанного в эту пирамиду? Итог урока. Где бы вы ни очутились после окончания школы, всюду вы встретите круглые тела: кирпич с отверстиями; графитные стержни; резервуары нефтеперерабатывающих заводов, ведра и подшипники, вулканы и их кратеры, воронки для переливания жидкостей и смерчи. Словом, вам придется самостоятельно моделировать жизненные ситуации.Эдгар Дейл в 1969 году выявил наиболее эффективные способы обучения.
Эдгар Дейл пришел к выводу, что:
– слушать лекции на тему или читать материалы по предмету – это наименее эффективный способ выучить что-либо; Результаты исследований он представил в виде схемы “Конус обучения”. Рефлексия.
4.4.Тест
Вариант №1 1. Конус может быть получен вращением… 1) равностороннего треугольника вокруг его стороны; 2) прямоугольного треугольника вокруг одного из его катетов; 3) прямоугольного треугольника вокруг гипотенузы.
2. Площадь боковой поверхности конуса можно вычислить по формуле…
1) 3. Сечением конуса плоскостью, перпендикулярной оси цилиндра, является… 1) треугольник; 2) прямоугольник; 3) круг. 4. Расстояние от центра основания конуса до плоскости сечения, проходящей через вершину конуса, равно длине отрезка…
1) OB; 2) OK; 3) OM.
1) сегмент; 2) сектор; 3) слой. 6. Площадь полной поверхности конуса равна…
1) 7. Наибольший периметр имеет сечение конуса, проходящее через его вершину и хорду, стягивающую дугу в… 1) 60°; 2) 90°; 3) 180°. 8. Через вершину конуса и хорду ВС проведена плоскость. Тогда угол между этой плоскостью и плоскостью основания это угол…
Вариант №2 1. Конус может быть получен вращением… 1) прямоугольного треугольника вокруг гипотенузы; 2) равнобедренного треугольника вокруг медианы, проведённой к основанию; 3) тупоугольного треугольника вокруг одной из его сторон. 2. Площадь боковой поверхности конуса нельзя вычислить по формуле…
1)
3. Сечением конуса плоскостью, проходящей вершину конуса и хорду 1) прямоугольный треугольник; 2) равнобедренный треугольник; 3) разносторонний треугольник. 4. Расстояние от центра основания конуса до плоскости сечения, проходящей через вершину конуса, равно длине отрезка… 1) OF; 2) OK; 3) OB. 5. а – образующая конуса, b – высота конуса. Тогда верно, что… 1) a > b; 2) a = b; 3) a < b. 6. Площадь полной поверхности конуса, у которого осевым сечением является равносторонний треугольник со стороной а, равна…
1) 7. Наибольшую площадь имеет сечение конуса, проходящее через его вершину и хорду, стягивающую дугу в…
8. Через вершину конуса и хорду AB проведена плоскость. Тогда угол между этой плоскостью и плоскостью основания – это угол… 1) ACB; 2) OAC; 3) CKO.
Ключ к тесту по теме: «Конус»
4.5. Практическая работа : Объём конуса. Цель: закрепить навык решения практических задач на вычисление объёма конуса. Теоретическая часть Прямым круговым конусом называется фигура, полученная при вращении прямоугольного треугольника вокруг оси содержащей один его катет.
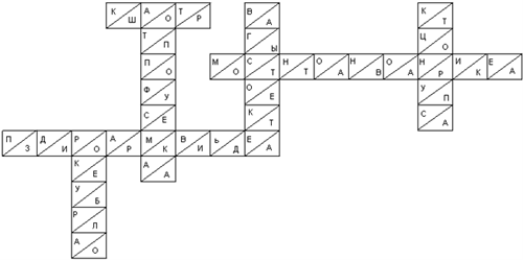
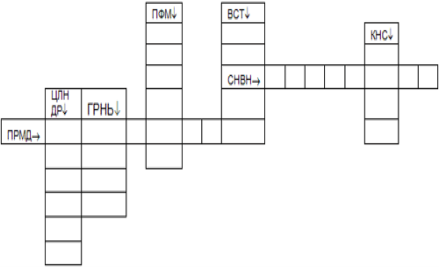
Выполните задания 1 вариант 1 уровень 1.Необходимо угадать принцип составления кроссворда и зашифрованные слова. Слова означают геометрические термины, относящиеся к стереометрии.
2 уровень
2. Высота конуса 4 см, радиус основания – 3 см. Найти образующую конуса.
3.Осевое сечение конуса – треугольник, все стороны которого равны 10 см. Найти угол наклона образующей к плоскости основании конуса.
4.Высота конуса 12 см, образующая – 13 см. Найти объём конуса.
5.Найти объем тела, полученного вращением прямоугольного треугольника с катетами 3 см и 4 см вокруг меньшего катета.
а) 16π см3; б) 24 π см3; в) 12 π см3; г) 9 π см3; д) 8 π см3. 3 уровень
8. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 16.
2 вариант 1 уровень 1.Необходимо угадать принцип составления кроссвордов и зашифрованные слова. Слова означают геометрические термины, относящиеся к стереометрии.
2 уровень
2. Высота конуса 6 см, радиус основания – 8 см. Найти образующую конуса.
3.Осевое сечение конуса – прямоугольный равнобедренный треугольник. Найти угол наклона образующей к плоскости основании конуса.
5.Найти объем тела, полученного вращением прямоугольного треугольника с катетом 12 см и гипотенузой 13 см вокруг меньшего катета.
6. Найдите объем конуса, площадь основания которого равна 2 см2, а образующая равна 6 см и наклонена к плоскости основания под углом 30 а) 16 см3; б) 2 см3; в) 12 π см3; г) 9 см3; д) 48 π см3.
8. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 81.
Критерии оценки практической работы
Максимальный балл за работу – 12 б.
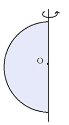
Тема 5. Шар
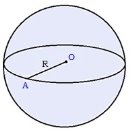
Цель: Сформировать представление о шар и ее элементы, сечение шара плоскостью и о касательную плоскость к шару, формировать умения и навыки учащихся решать задачи на использование шара и его элементов. Развивать пространственное воображение, наблюдательность и логическое мышление у учащихся. 5.1. Теория Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки. Поверхность шара называется сферой.
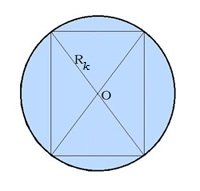
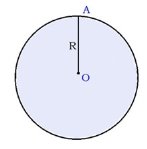
Сечение шара плоскостью, проходящей через центр шара, называется большим кругом. Для упрощения обычно рисуется не шар, а большой круг шара.
Площадь поверхности шара (т.е. сферы) вычисляется по формуле S(сферы) = 4⋅π⋅R2, где R - радиус шара.
Объём шара вычисляется по формуле V(шара) =
Всякое сечение шара плоскостью есть круг (или точка, если плоскость касается шара).
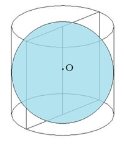
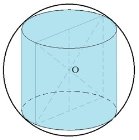
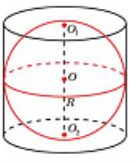
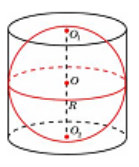
Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.
Общие элементы - две окружности.
рис. 1
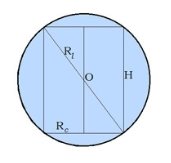
Чертится осевое сечение. В общем случае осевым сечением является равнобедренный треугольник (рис. 2)
Если дан равносторонний конус (у которого диаметр равен образующей), то осевым сечением является равносторонний треугольник (рис. 3).
Общие точки шара и куба - центры шести граней куба (точки касания шара и куба).
Определите отношение объёмов куба и вписанного в него шара.
Решение: V(куба) = a3, V(шара) = Если значение π принять за 3,14, то видно, что объём куба почти в два рза больше объёма вписанного в него шара.
π - иррациональное число, его приблизительное значение можно использовать только в том случае, если в задании указано оно само, или в задаче указывается, с какой точностью нужно вычислить величину.
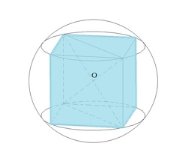
Общие точки шара и куба - восемь вершин куба.
При решении задач, в которых дан шар, описанный около куба, часто необходимо вычислять диагональ куба. Формула для вычисления диагонали прямоугольного параллелепипеда: d2=a2+b2+c2, где a, b, c - измерения прямоугольного параллелепипеда. У куба a = b = c, поэтому его диагональ можно вычислить с помощью формулы d=a√3, где а - ребро куба.
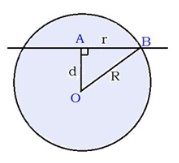
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью. Рисуется большой круг.
Круг с центорм A - основание шарового сегмента. AC = r - радиус основания шарового сегмента, AB = H - высота шарового сегмента, OC = R - радиус шара.
Площадь сферического сегмента вычисляется по формуле S(сегм.) = 2πRH
Объём шарового сегмента вычисляется по формуле
V(сегм.) =
В формулах для сегмента не используется радиус основания сегмента, а используется радиус шара.
5.2. Онлайн -ресурсы
http://ua.onlinemschool.com/math/assistance/figures_area_1/sphere/
http://ua.onlinemschool.com/math/assistance/figures_volume/sphere/
http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/ploschad-sfery
http://interneturok.ru/ru/school/geometry/11-klass/bobyomy-telb/ob-em-shara
https://www.youtube.com/watch?v=nLSwF0idE94
http://free.megacampus.ru/xbookM0001/index.html?go=part-069*page.htm
5.3. Урок Цели урока: образовательные:
Воспитательные:
Развивающие: совершенствование, развитие, углубление знаний, умений и навыков по теме; развитие пространственного воображения; развитие мыслительной деятельности: умения анализировать, обобщать, классифицировать. Оборудование: учебник геометрии; компьютер; мультимедейный проектор; модели геометрических фигур (шар, цилиндр); презентация.
Ход урока I. Организационный момент. Сообщить тему урока, сформулировать цели урока. II. Актуализация опорных знаний. 1) Устная работа. Соотнесите название фигуры и формулу объема и площади поверхности тел.
2) Проверка творческой домашней работы. III. Изучение новой темы. Сегодня мы с вами выведем формулу для вычисления объема шара. Вспомните, определение шара и его элементов. (Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.)
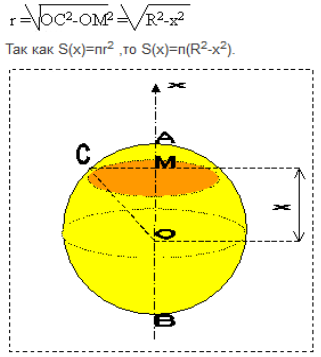
Теорема: Объем шара равен Доказательство: Мы уже знаем, что можно вычислять объемы тел с помощью интегральной формулы
Давайте посмотрим, как это можно сделать для вывода формулы объема шара. (Учитель объясняет вывод формулы объема шара с помощью формулы, ученики делают записи в тетрадях.) Рассмотрим шар радиуса R с центром в точке О и выберем ось ОХ произвольным образом. Сечение шара плоскостью, перпендикулярной к оси ОХ и проходящий через точку М этой оси, является кругом с центом в точке М.. Обозначим радиус этого круга через r, а его площадь через S(х), где х абсцисса точки М. Выразим S(х) через х и R. Из прямоугольного треугольника ОМС находим
Заметим, что эта формула верна для любого положения точки М на диаметре АВ, т.е. для всех х, удовлетворяющих условию
Теорема доказана. Физкультминутка (для глаз). IV. Формирование умений и навыков учащихся. Проблемная задача. При уличной торговле арбузами весы отсутствовали. Однако выход был найден: арбуз диаметром 3 дм приравнивали по стоимости к трем арбузам диаметром 1 дм. Что вы возьмете? Правы ли были продавцы?
Задача (Архимеда): Дано: в цилиндр вписан шар. Найти: отношение объемов цилиндра и шара. Ответ: 1,5.
1. Около шара описан цилиндр, площадь поверхности которого равна 18. Найдите площадь поверхности шара. Решение: (Опираемся на открытие Архимеда.) Ответ: 12 2. Площадь поверхности шара уменьшили 9 раз. Во сколько раз уменьшился объем шара? Решение: Пусть радиус первого шара R, а уменьшенного r.
V. Итог урока. Оценить работу учащихся на уроке и выставить оценки. Диагностика (рефлексия). На сегодняшнем уроке мы с вами вывели формулу объема шара, выяснили, что данные тела имеют широкое практическое применение и сделали небольшое открытие, которое еще в 3 веке до нашей эры сделал Архимед. Беседа по следующим вопросам:
Что было интересного сегодня на уроке? Что вызвало трудности? Какие умения приобрели сегодня? Где могут пригодиться эти умения?
Домашнее задание.
5.4. Практическая работа Цель: закрепить навык решения практических задач на вычисление объёма шара. Теоретическая часть
Сферой называется множество точек пространства, находящихся на одинаковом расстоянии
Части шара
Выполните задания 1 вариант 1 уровень
Ответьте на вопросы теста, выбрав один ответ из числа предложенных. 1. Сколько диаметров у сферы? а) 1; б) 3; в)2; г) бесконечно много. 2. Какой фигурой является сечение шара плоскостью? а) отрезком; б) кругом; в) окружностью; г) сферой. 3. Если радиус сферы увеличить в 2 раза, то объём увеличиться. а) в 2 раза; б) в 8 раз; в) в 4 раза; г) в 16 раз.
4. По формуле а) шара; б) цилиндра; в) конуса; г) шарового сектора.
5. Радиус шара равен 3 см. Найдите объём шара. а)36π см3; б) 12π см3; в) 36 см3; г) 45π см3.
2 уровень 6. Найдите расстояние от центра шара до плоскости сечения, если объём шара равен 288π, а площадь сечения равна 27π. а) 2√3; б) 3; в) 4; г) 6; д) 3√2. 7. Найдите объём шара, площадь поверхности которого равна 108π см2. а) 108π см3; б) 108π√2 см3; в) 81√3 π см3; г) 81π см3; д) 108√3 π см3.
8. Диаметр одного шара равен радиусу другого. Найдите отношение объёмов этих шаров. а) 1 : 2; б) 2 : 1; в) 4 : 1; г) 1 : 8; д) 8 : 1. 9. Площадь большого круга шара равна 3π см2. Найдите объём шара.
а)
3 уровень
10. Прямоугольный параллелепипед описан около сферы радиуса
11. Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов. 12. Найдите объём шарового сектора, если радиус шара равен 3√2 см, а радиус окружности основания - √10 см. а) 36√2 π см3; б) 12√2 π см3; в) 6√2 π см3; г) 8√2 π см3; д) 4√2 π см3.
2 вариант 1 уровень
Ответьте на вопросы теста, выбрав один ответ из числа предложенных.
1. Сколько радиусов у сферы? а) 1; б) 3; в)2; г) бесконечно много. 2. Какой фигурой является сечение шара плоскостью? а) отрезком; б) кругом; в) окружностью; г) сферой. 3. Если радиус сферы увеличить в 3 раза то объём увеличиться а) в 2 раза; б) в 8 раз; в) в 27 раз; г) в 16 раз.
4. По формуле а) сферы; б) цилиндра; в) конуса; г) шарового сектора. 5. Радиус шара равен 6 см. Найдите объём шара. а)36π см3; б) 12π см3; в) 36 см3; г) 288π см3.
2 уровень 6. Найдите расстояние от центра шара до плоскости сечения, если объём шара равен 288π, а площадь сечения равна 16π. а) 2√5; б) 3; в) 4; г) 6; д) 3√2. 7. Объем шара равен 36π. Найти площадь его поверхности. а) 108π см2; б) 108π√2 см2; в) 81√3 π см2; г) 36π см2; д) 108√3 π см2. 8. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго? а) в 27 раз; б) в 9 раз; в) в 3 раза; г) в 2 раза; д) в 4 раза. 9. Площадь большого круга шара равна 9π см2. Найдите объём шара.
а) 3 уровень 10. Прямоугольный параллелепипед описан около сферы радиуса 9,5.
11. Радиусы трех шаров равны 3, 4 и 5. Найдите радиус шара, объем которого равен сумме их объемов. 12. Определить объём шарового сектора, если радиус окружности его основания равен 60 см, а радиус шара равен 75 см. а) 125π см3; б) 112500 π см3; в) 1125π см3; г) 2500 π см3; д) 112550 π см3.
Критерии оценки практической работы
Максимальный балл за работу – 12 б.
Тема 6. Итогоая 6.1. Урок: Решение практических задач на вычисление объёмов тел вращения. 6.2.Зачетная работа
Ответы 1В. 4,5; 5989,5; 234; 17; 52; 129; 26; 100. 2В. 562,5; 288; 180; 37; 62; 21; 20; 20.
6.3 Практическая работа Тела вращения. Цель: закрепить навык решения практических задач на вычисление объёмов и площадей тел вращения. Теоретическая часть
Выполните задания 1 вариант 1 уровень
А. Конической; Б. Концентрической; В. Цилиндрической; Г. Сферической.
А. Треугольник; Б. Круг; В. Прямоугольник; Г. Трапеция.
R – радиус, H – высота:
А. 2πRl; Б.
А. Образующая; Б. Ось; В. Высота; Г. Медиана.
А. Конуса; Б. Усеченного конуса; В. Цилиндра; Г. Шара.
А. 7.Сколько можно провести диаметров через точку, произвольно взятую внутри шара? А. Одну. Б. Ни одной. В. Две. Г. Бесконечно много. 8. Проекцией тела в горизонтальной плоскости является круг, а в вертикальной плоскости – равнобедренный треугольник. Определите форму тела. А. Цилиндр; Б. Пирамида; В. Конус; Г. Шар. 9. Как изменится объем шара, если радиус увеличить в 2 раза? А. Увеличится в 8 раз; Б. Не изменится; В. Увеличится в 4 раза; Г. Увеличится в 2 раза. 10. Радиус шара 1 м. Вычислите объем шара.
А. 2 уровень 11. Если высота конуса 15 см, а радиус основания 8 см, то образующая конуса равна: А. 14 см; Б. 17 см; В. 13 см; Г. 6 см. 12.Секущая плоскость удалена от центра шара на расстояние 8 см, а радиус шара равен 10 см. Вычислите площадь сечения шара.
А. 13.Образующая конуса равна 10 см, а диаметр основания – 12 см. Вычислите площадь осевого сечения конуса.
А. 24 см 14.Образующая конуса равна 7 см, а высота – 6 см. Вычислите объем конуса.
А. 15. Равнобедренный треугольник с основанием 8 см и боковыми сторонами по 5 см вращается вокруг высоты, проведенной к основанию. Вычислите объем тела вращения.
А. 16.В цилиндрическую банку диаметром 10 см опустили в жидкость деталь. Вычислите объем детали, если высота жидкости в банке поднялась на 4 см.
А. 17.Прямоугольник со сторонами 5 см и 4 см вращается вокруг большей стороны. Вычислите объем тела вращения.
А.
3 уровень
18. Образующая конуса равна 4 дм и наклонена к основанию под углом 60
А. 19.Объем и площадь поверхности шара выражены одним и тем же числом. Вычислите радиус шара. А. 3; Б. 4; В. 5; Г. 6. 20.В шар вписан прямоугольный параллелепипед с измерениями 6 см, 3 см и 2 см. Вычислите радиус шара. А. 1,5 см; Б. 2 см; В. 3 см; Г. 3,5 см. 21.Диаметр цилиндра равен 6 см, а высота – 10 см. Вычислите площадь его боковой поверхности.
А. 30 22. Высота цилиндра равна 10 см, а радиус его основания – 5 см. Плоскость пересекает цилиндр параллельно его оси и удалена от нее на 4 см. Вычислите площадь сечения.
А. 60 см
2 вариант 1 уровень
А. Апофема; Б. Высота; В. Образующая; Г. Радиус.
H - высота:
А.
А. Прямоугольника вокруг одной из сторон; Б. Равностороннего треугольника вокруг медианы; В. Прямоугольного треугольника вокруг одного из катетов; Г. Равнобедренного треугольника вокруг высоты.
l – образующая, R – радиус, H – высота:
А.
А. Одну общую точку; Б. Ни одной общей точки; В. Две общие точки; Г. Много общих точек.
А. 2 м2; Б. 3 м2; В. 4 м2; Г. 5 м2 .
А. Одна. Б. Ни одной. В. Две. Г. Бесчисленное множество. 9. В горизонтальной и вертикальной плоскости проекциями тела являются круги. Определите форму тела. А. Конус; Б. Цилиндр; В. Шар; Г. Усеченный конус. 10. Радиус цилиндра увеличили в два раза, а высоту уменьшили в два раза. Как изменится объем цилиндра? А. Увеличится в 2 раза. Б. Уменьшится в 2 раза. В. Не изменится. Г. Увеличится в 4 раза.
2 уровень
11. Радиус основания конуса равен 6 см, а высота – 8 см. Вычислите его образующую. А. 10 см; Б. 20 см; В. 15 см; Г. 25 см. 12. Радиус шара 12 см. На касательной плоскости лежит точка К, которая удалена от точки касания на 5 см. На каком расстоянии находится точка К от поверхности шара? А. 1 см; Б. 2 см; В. 0,5 см; Г. 13 см.
13. Образующая конуса равна 12 см и наклонена к основанию под углом 30 А. 8 см; Б. 6 см; В. 10 см; Г. 4 см. 14. Высота равностороннего цилиндра равна 10 см. Вычислите его объем.
А. 15. Площадь осевого сечения цилиндра равна S. Вычислите площадь боковой поверхности цилиндра.
А. 2S; Б. 3S; В. 3,5S; Г. 16. Как изменится площадь поверхности шара, если радиус увеличить в 3 раза? А. Увеличится в 3 раза; Б. Не изменится; В. Увеличится в 9 раз; Г. Уменьшится в 9 раз. 17. Прямоугольник со сторонами 6 см и 4 см вращается сначала вокруг меньшей стороны, а затем – большей. Одинаковы ли объемы тел вращения? А. Да; Б. Нет;
3уровень 18. Около прямоугольного параллелепипеда, измерения которого равны 2 см, 4 см и 4 см описана сфера. Вычислите площадь поверхности сферы.
А.
19.Через середину высоты конуса и перпендикулярно ей построено сечение плоскостью. Площадь сечения равна 8 см
А. 23 см
20.Образующая конуса наклонена к основанию под углом 60
А. 21.Высота равностороннего цилиндра равна 6 дм. Вычислите площадь боковой поверхности цилиндра.
А. 16 22. На окраску шара диаметром 2 дм требуется 20 г краски. Сколько краски потребуется для окраски шара диаметром 6 дм? А. 60 г; Б. 120 г; В. 180 г; Г. 240 г.
Критерии оценки практической работы
Максимальный балл за работу – 11 б.
6.4 . Урок-зачет по теме «Объемы тел»
Оборудование: карточки для проведения зачета Ход урока. I.Организационный момент. II.Зачет Билет 1. 1.Понятие объема. Свойства объемов. 2.Теорема об объеме шара. 3.Задача. Сторона основания правильной шестиугольной пирамиды равна 4,а угол между боковой гранью и основанием равен 450 Найти объем пирамиды. Билет 2. 1.Понятие призмы вписанной в цилиндр, описанной около цилиндра .Формула для нахождения объема цилиндра. 2.Теорема об объеме прямой призмы. 3.Задача В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить в другой цилиндрический сосуд, диаметр которого в 3 раза больше первого?
Билет 3. 1.Понятие шарового сегмента. Объем шарового сегмента. 2.Теорема об объеме пирамиды. 3. Задача. Найти объем V конуса, образующая которого равна 10 и наклонена к плоскости основания под углом 30. В ответе укажите V/π
Билет 4. 1.Понятие шарового слоя. Объем шарового слоя. 2.Теорема об объеме конуса. 3. Задача.
Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны
Билет 5 1.Понятие шарового сектора. Объем шарового сектора. 2.Теорема об объем цилиндра. 3. Задача. Во сколько раз объем конуса, описанного около правильной четырехугольной пирамиды , больше объема конуса ,вписанного в эту пирамиду.
Билет 6. 1.Объем прямоугольного параллелепипеда. 2.Теорема об объеме наклонной призмы. 3.Задача. Объем куба равен 150. Найдите объем четырех угольной пирамиды, основанием которой является грань куба, а вершиной - центр куба.
III .Итог урока Вопросы для подготовки к зачету. 1.Понятие объема. 2.Свойства объемов. 3.Объем прямоугольного параллелепипеда. 4.Объем прямой призмы. 5.Теорема об объеме прямой призмы. 6.Теорема об объеме цилиндра. 7.Теорема об объеме наклонной призмы. 8.Теорема об объеме пирамиды. 9.Теорема об объеме конуса. 10.Теорема об объеме шара. 11.Шаровой сегмент. Объем шарового сегмента. 12.Шаровой слой. Объем шарового слоя. 13.Шаровой сектор. Объем шарового сектора. 14.Площадь сферы.
Задачи для проведения зачета. 1.В сосуд, имеющий форму правильной треугольной призмы, налили 600 см3 воды и полностью погрузили в нее деталь. При этом уровень воды в сосуде поднялся с отметки 12 см до 16 см. Чему равен объем детали. 2.Сторона основания правильной четырехугольной пирамиды равна 16,боковые ребра 17. Найти объем пирамиды. 3.Кубик весит 8 г. Сколько граммов будет весить кубик, ребро которого в 3,5 больше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала. 4.Цилиндр и конус имеют общее основание и высоту. Вычислите объем цилиндра, если объем конуса равен 10. 5.Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равна 2. Найти объем параллелепипеда. 6.Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 600 . Высота пирамиды равна 6. Найдите объем пирамиды. 7.Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 1. Объем параллелепипеда равен 8. Найти высоту цилиндра. 8.Основанием прямой призмы является прямоугольный треугольник с катетами 1 и 5.Боковые ребра равны 8/π Найдите объем цилиндра, описанного около этой призмы.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Заключение.
Сегодня дистанционное обучение через Интернет все чаще рассматривается не просто как удобная форма повышения квалификации, а как вполне серьезная альтернатива традиционному образованию, позволяющая обучающемуся получить глубокие знания. Если знание — сила, то дистанционное обучение вполне может стать самым сильным соперником среди инструментальных средств обучения высоким технологиям.
Работы с дистанционными образовательными ресурсами позволяет отметить следующие преимущества:
- максимальная индивидуализация учебного процесса обучающихся;
- ориентация учащихся на процесс самообразования;
- гибкость организационной структуры обучения с использованием дистанционных образовательных технологий;
- разноуровнивость содержания образовательного ресурса;
- дифференцированный подход к учащимся;
Подводя итог, хотелось бы сказать, что распространение различных форм дистанционного образования – это естественный и необходимый этап в развитии современной системы образования. Оно призвано не исключать, а дополнять традиционные формы обучения.

про публікацію авторської розробки
Додати розробку