Тема уроку.   Кут між мимобіжними прямими.

Мета уроку: формування поняття кута між мимобіжними прямими, а також вмінь учнів знаходити кути між мимобіжними прямими.

Обладнання: стереометричний набір, моделі куба, тетраедра, прямокутного паралелепіпеда.

Хід уроку

I. Аналіз виконання тематичного оцінювання № 5

II. Перевірка домашнього завдання

В кінці уроку збираються учнівські зошити для перевірки їх ведення і виконання домашнього завдання.

III. Сприйняття й усвідомлення нового матеріалу

Поняття кута між прямими, які перетинаються

Введемо поняття кута між прямими в просторі.

Якщо дві прямі перетинаються, вони утворюють чотири кути (по­парно вертикальні або попарно суміжні). Кутова міра меншого з них називається кутом між даними прямими, що перетинаються. Кут між прямими, що перетинаються, не перевищує 90° .

Якщо прямі перпендикулярні, то величина кута між цими прямими дорівнює 90° .

Кут між паралельними прямими вважають таким, що дорівнює 0°. Слід зазначити, що кут між прямими — це не геометрична фігура, це — величина.

Розв'язування вправ

1. ABCDA₁B₁С₁D₁ — куб. Знайдіть кут між прямими:

а) АВ₁ і AD₁; б) АВ₁ і AD;  в) АВ₁ і АВ;   г) АС і AC₁.

(Відповідь: а) 60° ; б) 90° ; в) 45° ; г) arcsin .)

2. Прямі а і b перетинаються під кутом 30° , а прямі а і с — під кутом 60° . Чи можуть бути перпендикулярними прямі b і с? (Відповідь. Так.)

3. ABCDA₁B₁C₁D₁ — прямокутний паралелепіпед, в якому АВ = а, AD = b, АА₁ = с . Знайдіть кут між прямими:

а) А₁В і АВ;   б) A₁D і AD;  в) BD і АВ;    г) ВА₁ і DA₁.

(Відповідь, a) arctg ; б) arctg; в) arctg ; г) arccos .)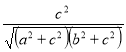

Кут між мимобіжними прямими

Кутом між мимобіжними прямими називається кут між пря­мими, які перетинаються і паралельні відповідно даним мимобіж­ним прямим.

Кут між мимобіжними прямими, як і між прямими однієї площини, не може бути більше 90°. Дві мимобіжні прямі, які утворюють кут в 90° , називаються перпендикулярними.

Розв'язування вправ

1. Покажіть перпендикулярні мимобіжні прямі в оточенні.

2. Дано зображення куба (рис. 275). Знайдіть кут між мимобіжними прямими а і b.

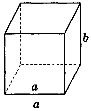
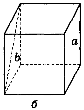
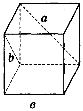
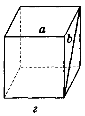
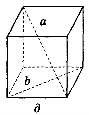
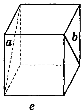
Рис. 275

(Відповідь, а) 90°; б) 45° ; в) 60°; г) 90°; д) 90°; е) 90°.)

3. Дано куб ABCDA₁B₁C₁D₁. Доведіть, що АВ₁ CD₁.

4. Пряма SA перпендикулярна до сторін АВ і АС трикутника АВС. Знайти кут між прямими SA і ВС. (Відповідь. 90°.)

5. Точки К і М середини ребер АВ і DC трикутної піраміди DABC, кожне ребро якої дорівнює а. Доведіть, що KM АВ. Знайдіть довжину відрізка KM.

(Відповідь. .)

6. Знайдіть кут між мимобіжними діагоналлю грані куба і діагоналлю куба.

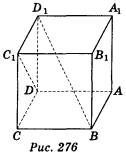Розв'язання

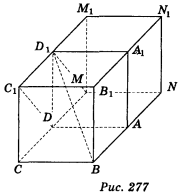
Знайдемо кут між діагоналлю ВD₁ куба і діагоналлю DC₁ грані куба (рис. 276). Добудуємо до даного куба куб ADMNA₁D₁M₁N₁ (рис. 277), тоді кут між прямими BD₁ і DC₁ дорівнює куту між прямими BD₁ і D₁M . Нехай АВ = а; тоді D₁M = а, AD₁ = a , ВМ = а .

Із ΔBD₁M маємо:

ВМ² = DB² + D₁M² – 2AD₁ · D₁M cosBD₁M , або

5а² = 2а² + 3а² – 2а · a cos BD₁M ;  

5а² = 5а² – 2а² cos <BD₁M;

2а² cos <BD₁M = 0 ;

cos <BD₁M = 0 ;

<BD₁M = arccos 0 = 90°.

Відповідь. 90° .

7. Довести, що кут між мимобіжними прямими не залежить від вибо­ру прямих, що перетинаються.

IV. Узагальнення та систематизація знань

Враховуючи означення кута між мимобіжними прямими, можна дати узагальнене означення перпендикулярності прямої і площини, ознаки пе­рпендикулярності прямої і площини, теореми про три перпендикуляри.

Якщо пряма перпендикулярна до площини, то вона перпе­ндикулярна до будь-якої прямої, що лежить у цій площині.

Ознака перпендикулярності прямої і площини

Якщо пряма перетинає площину, перпендикулярна до двох прямих цієї площини, що перетинаються, то вона перпен­дикулярна до площини.

Узагальнена теорема про три перпендикуляри

Будь-яка пряма на площині, перпендикулярна до проекції по­хилої на цю площину, перпендикулярна і до похилої. І навпа­ки: якщо пряма на площині перпендикулярна до похилої, то вона перпендикулярна і до проекції похилої.

Розв'язування задач

1. Задача № 30 із підручника (с. 56).
2. Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що перетинаються, то вона перпендикулярна до площини. Довести.
3. Задача № 33 із підручника (с. 56).
4. Дано куб ABCDA₁B₁C₁D₁. Доведіть, що АС₁ 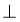BD.
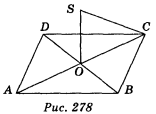
5. ABCD — ромб (рис. 278), пряма SO пер­пендикулярна до площини АВС. Дове­діть, що SC 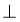BD .
6. SABC — трикутна піраміда, всі ребра якої рівні. Доведіть, що SA 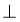ВС.

V. Домашнє завдання

§ 4, п. 31; контрольне запитання № 14; задача № 32 (с. 56).

VI. Підведення підсумку уроку

Запитання до класу

1. Що називається кутом між мимобіжними прямими?
2. Чи залежить кут між мимобіжними прямими від вибору прямих, які перетинаються?
3. Сформулюйте узагальнене означення перпендикулярності прямої і площини.
4. Сформулюйте узагальнену ознаку перпендикулярності прямої і площини.
5. Сформулюйте узагальнену теорему про три перпендикуляри.