Кут між прямою і площиною. Кут між площинами. Перпендикулярність площин. Ознака перпендикулярності площин.
Тема. Кут між прямою і площиною. Кут між площинами. Перпендикулярність площин. Ознака перпендикулярності площин.
Мета: сформувати поняття кута між прямою і площиною, двогранного кута, кута між площинами, лінійного кута двогранного кута, про перпендикулярні площини, про ознаку перпендикулярності площин, уміння застосовувати зазначені означення й ознаку для розв'язання задач; сформувати вміння знаходити кути між прямою і площиною, кут між площинами, лінійний кут двогранного кута; розвиток логічного мислення; виховувати наполегливість, відповідальність, уважність.
Тип уроку: засвоєння нових знань, формування вмінь.
Тема. Кут між прямою і площиною. Кут між площинами. Перпендикулярність площин. Ознака перпендикулярності площин.
Мета: сформувати поняття кута між прямою і площиною, двогранного кута, кута між площинами, лінійного кута двогранного кута, про перпендикулярні площини, про ознаку перпендикулярності площин, уміння застосовувати зазначені означення й ознаку для розв’язання задач; сформувати вміння знаходити кути між прямою і площиною, кут між площинами, лінійний кут двогранного кута; розвиток логічного мислення; виховувати наполегливість, відповідальність, уважність.
Тип уроку: засвоєння нових знань, формування вмінь.
Обладнання: конспект, підручник Г.П. Бевз Геометрія 10 клас профільний рівень, модель куба.
Література:
- Для вчителя:
Г.П. Бевз Геометрія 10 клас профільний рівень;
Є.П. Нелін Геометрія 10 клас.
- Для учнів:
Г.П. Бевз Геометрія 10 клас профільний рівень.
Хід уроку
I. Організаційний етап.
Вітаюсь, перевірка присутності учнів і готовність аудиторії до уроку.
II. Перевірка домашнього завдання.
III. Актуалізація опорних знань.
Запитання до класу:
1. Дано дві прямі, що перетинаються:
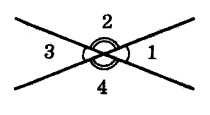
А) Які кути утворилися при їх перетині? (Суміжні та вертикальні)
Б) Які властивості мають ці кути? (Вертикальні рівні, а сума суміжних = 180)
2. Чому дорівнює кут між паралельними прямими? (Нулю, за означенням)
3. Яким є взаємне розміщення прямих у просторі?
4. Що називають кутом між прямими?
5. Сформулюйте ознаку перпендикулярності прямої і площини.
IV. Засвоєння знань.
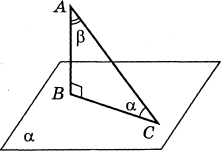
Кутом між прямою та площиною називається кут між цією прямою і її проекцією на площину.
Якщо пряма перпендикулярна до площини, то кут між нею й площиною вважається таким, що дорівнює 90 градусів, а між паралельними прямою та площиною таким, що дорівнює 0 градусів.
Кут між прямою та площиною і кут між цією прямою й перпендикуляром до площини в сумі дорівнює 90 градусів.
На рисунку ![]() .
.
Нехай дані площини перетинаються. Проведемо площину, перпендикулярну до прямої їх перетину. Ця площина перетинає дані площини по двох прямих. Кут між цими прямими називається кутом між даними площинами.
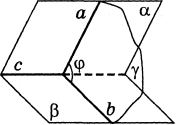
Кутом між площинами, які перетинаються , називається кут між прямими, проведеними в цих площинах перпендикулярно до лінії їх перетину.
Якщо площини паралельні то вважають, що кут між ними дорівнює нуль градусів.
Кут між площинами ![]() і
і ![]() позначають
позначають ![]() .
.
Він набуває значень у тих самих межах, що і кут між прямими: ![]() .
.
Дві площини називаються перпендикулярними, якщо кут між ними дорівнює 90 градусів.
Теорема (Ознака перпендикулярності площин)
Якщо одна з двох площин проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.
Доведення
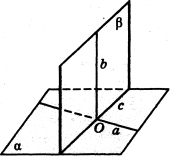
Нехай площина ![]() проходить через пряму
проходить через пряму ![]() , перпендикулярну до площини
, перпендикулярну до площини ![]() , Доведемо, що
, Доведемо, що ![]() .
.
1. Пряма ![]() перетинає площину
перетинає площину ![]() у деякій точці
у деякій точці ![]() .
.
2. Ця точка спільна для площин ![]() і
і ![]() .
.
3. ![]() ,
, ![]() .
.
4. Проведемо у площині ![]() через точку
через точку ![]() пряму
пряму ![]() , перпендикулярну до
, перпендикулярну до ![]() .
.
5. Оскільки ![]() і
і ![]() лежать у площині
лежать у площині ![]() і
і ![]() , то
, то ![]() і
і ![]() .
.
6. Отже, ![]() , тобто
, тобто ![]() . Що і треба було довести.
. Що і треба було довести.
Двогранним кутом називають частину простору, обмежену двома півплощинами, які виходять з однієї прямої.
Цю пряму називають ребром двогранного кута.

Дві площини, які виходять з однієї прямої, також називають двогранним кутом.
Перерізом двогранного кута площиною, перпендикулярною до його ребра, є кут. Його називають лінійним кутом даного двогранного кута.
За міру двогранного кута приймається міра його лінійного кута.
Градусна міра двогранного кута лежить у межах від ![]() до
до ![]() .
.
V. Закріплення нового матеріалу.
Усні вправи:
1) Кут між прямою і площиною = ![]() . Який кут утворить дана пряма з перпендикуляром до даної площини? (
. Який кут утворить дана пряма з перпендикуляром до даної площини? (![]() )
)
2) Точка ![]() не належить площині
не належить площині ![]() . Скільки прямих, нахилених до площини
. Скільки прямих, нахилених до площини ![]() під кутом
під кутом ![]() , можна провести через точку
, можна провести через точку ![]() ? (Безліч)
? (Безліч)
3) Дано дві паралельні прямі, проведені до тієї самої площини. Що можна сказати про величину кутів, які вони утворять із площиною? (однакова величина кутів)
Задача 1.
З точок ![]() і
і ![]() , які лежать у двох перпендикулярних площинах, опущені перпендикуляри
, які лежать у двох перпендикулярних площинах, опущені перпендикуляри ![]() і
і ![]() на пряму перетину площин. Знайдіть довжину відрізка
на пряму перетину площин. Знайдіть довжину відрізка ![]() , якщо
, якщо ![]() см,
см, ![]() см,
см, ![]() см.
см.
Розв’язання
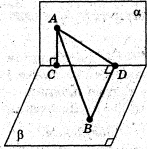
Оскільки ![]() і
і ![]() , то
, то ![]() і
і ![]() . Із трикутника
. Із трикутника ![]()
![]() маємо:
маємо: ![]() . Із трикутника
. Із трикутника ![]()
![]() маємо:
маємо: ![]() (см).
(см).
Задача 2.
![]() - куб. Побудуйте перерізи куба площинами
- куб. Побудуйте перерізи куба площинами ![]() і
і ![]() Доведіть, що площини перерізів перпендикулярні.
Доведіть, що площини перерізів перпендикулярні.
Розв’язання
Доведемо, що ![]()
![]()
![]() .
.
Розглянемо площини ![]() і
і ![]() . Пряма
. Пряма ![]() ; Пряма
; Пряма ![]() .
. ![]() ,
, ![]() ;
; ![]() ,
, ![]() - як діагоналі квадрата
- як діагоналі квадрата ![]() ;
;
Тоді за теоремою ознака перпендикулярності площин ![]()
![]()
![]() , що і треба було довести.
, що і треба було довести.
Задача 3.
На одній із граней гострого двогранного кута позначено точку ![]() на відстані
на відстані ![]() см від ребра кута. Знайдіть величину двогранного кута, якщо дана точка віддалена від іншої грані на
см від ребра кута. Знайдіть величину двогранного кута, якщо дана точка віддалена від іншої грані на ![]() см.
см.
Розв’язання
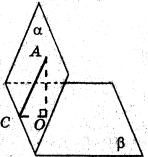
Нехай точка ![]() лежить у грані
лежить у грані ![]() даного двогранного кута. Проведемо
даного двогранного кута. Проведемо ![]() ;
; ![]() - відстань від точки
- відстань від точки ![]() до грані
до грані ![]() ;
; ![]() см. Проведемо
см. Проведемо ![]()
![]() - відстань від точки
- відстань від точки ![]() до ребра кута,
до ребра кута, ![]() см.
см.
![]() - проекція
- проекція ![]() на площину
на площину ![]() ;
; ![]() за теоремою про три перпендикуляри. Тоді кут
за теоремою про три перпендикуляри. Тоді кут ![]() - лінійний кут двогранного кута. Із
- лінійний кут двогранного кута. Із ![]()
![]() маємо:
маємо: ![]() ,
, ![]() звідки
звідки ![]() .
.
VI. Підбиття підсумків уроку.
Запитання до класу:
1. Дайте означення кута між прямою і площиною.
2. Що називається кутом між площинами?
3. Які площини називаються перпендикулярними?
4. Сформулюйте ознаку перпендикулярності площин.
VII. Домашнє завдання.
Вивчити конспект, §15, № 350, 352, 360.

про публікацію авторської розробки
Додати розробку
