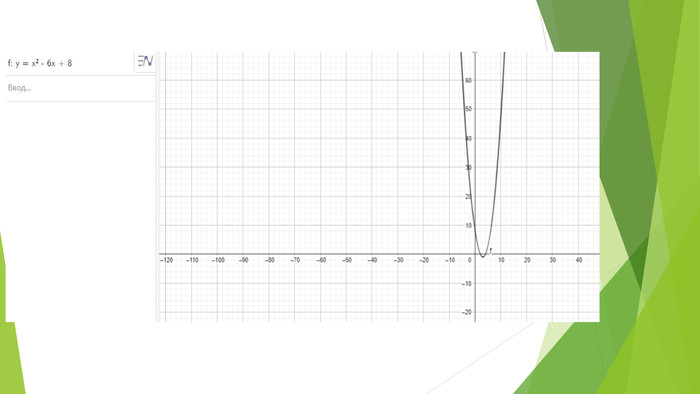
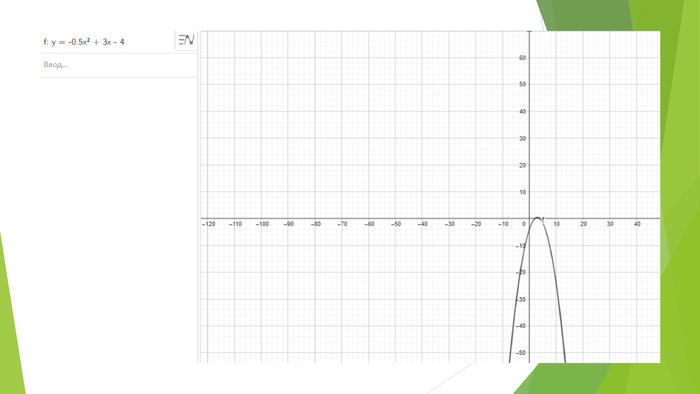
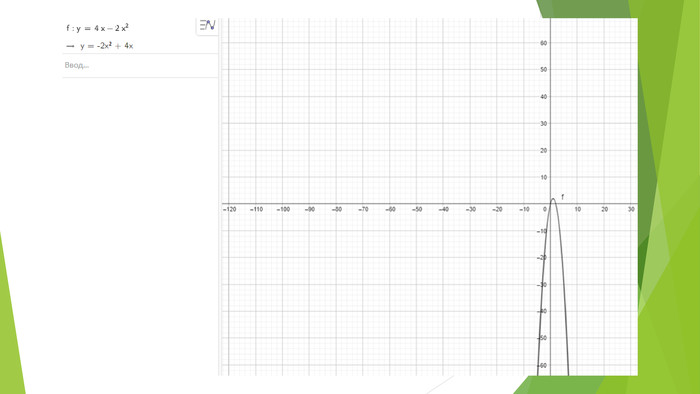
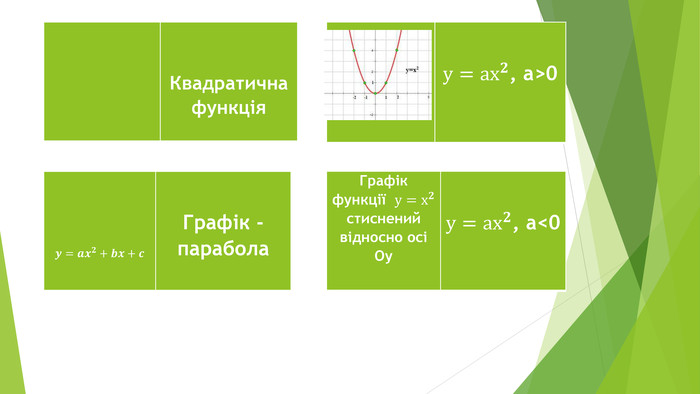
Квадратична функція, її графік а властивості
Про матеріал
Розробка дистанційного уроку з алгебри у 9 класі. Урок застосування знань, вмінь, навичок. Використані ресурси:
LearningApps, GeoGebra. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 9 клас (Бевз Г.П., Бевз В.Г.)
До уроку
Розділ 2. КВАДРАТИЧНА ФУНКЦІЯ Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку







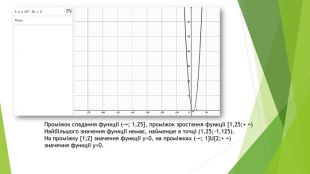
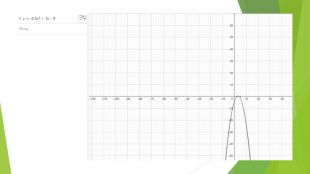
![Проміжок спадання функції (-∞; 1,25], проміжок зростання функції [1,25;+ ∞)Найбільшого значення функції немає, найменше в точці (1,25;-1,125). На проміжку [1;2] значення функції у<0, на проміжках (-∞; 1]U[2;+ ∞) значення функції y>0. Проміжок спадання функції (-∞; 1,25], проміжок зростання функції [1,25;+ ∞)Найбільшого значення функції немає, найменше в точці (1,25;-1,125). На проміжку [1;2] значення функції у<0, на проміжках (-∞; 1]U[2;+ ∞) значення функції y>0.](/uploads/files/489231/207804/223692_images/9.jpg)