Презентація" Квадратична функція та її графік"
Про матеріал
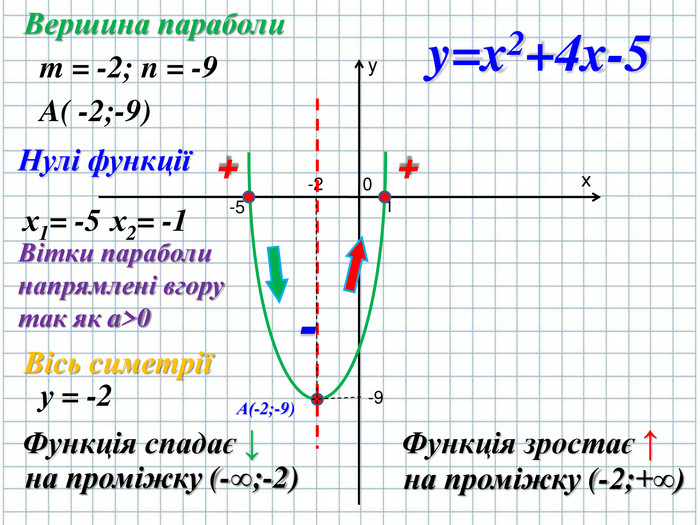
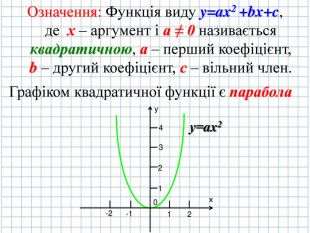
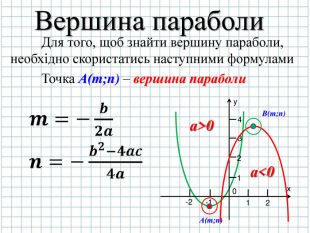
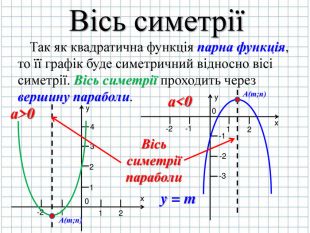
Тема презентації "Квадратична функція та її графік". Презентація створена до уроку алгебри для 9 класу закладів загальної середньої освіти.За підручником Алгебра: підручник для 9 класу загал. навч. закладів/ Н.С.Прокопенко, Ю.О.Захарійченко, Н.Л.Кінащук. - Харків: Вид-во "Ранок",2017
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Прокопенко Н.С., Захарійченко Ю.О., Кінащук Н.Л.)
До уроку
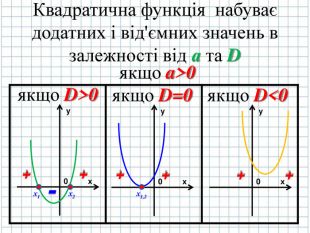
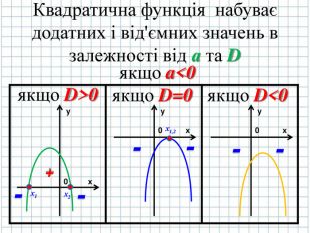
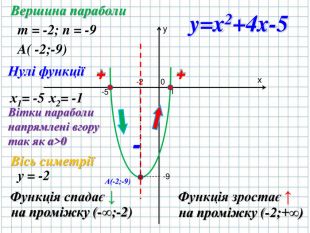
РОЗДІЛ 2. КВАДРАТИЧНА ФУНКЦІЯ Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку














-

Лебедева Юля
28.06.2023 в 19:32
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Volchkova Maria Ivanivna
05.11.2020 в 21:34
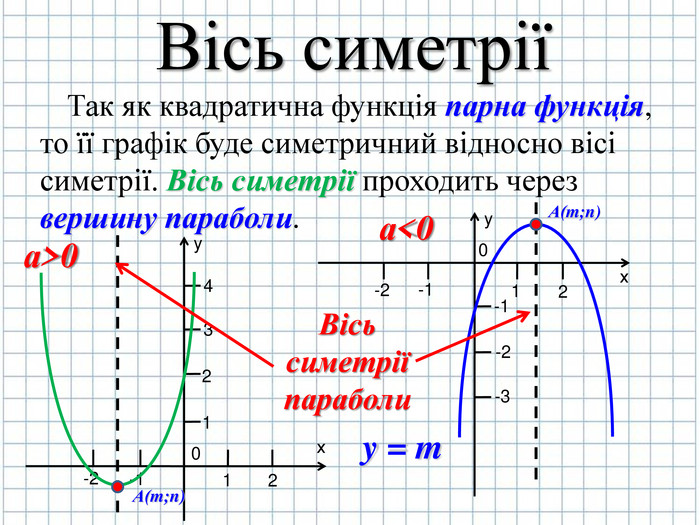
Дякую за працю. Маленька описка: вісь симетрії х=-2
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Орина Барзік Сергіївна
12.10.2020 в 20:27
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

МАКЕДОНСЬКА ЛЮДМИЛА
15.09.2020 в 20:57
Загальна:
4.7
Структурованість
5.0
Оригінальність викладу
4.0
Відповідність темі
5.0
Показати ще 1 відгук