Квадратична функція і нерівність
Контрольна робота орієнтована на перевірку знань учнів з тем "Квадратична функція" і "Квадратна нерівність"
Робота включає в себе різнотипні завдання різної складності. Форма роботи - ЗНО
Варіант 1
-
Графік функції
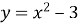зміщений ….. .
|
А) вправо |
Б) вверх |
В) вниз |
Г) вліво |
-
Графік функції
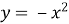є …. .
|
А) звуженим |
Б) вітки вверх |
В) розширеним |
Г) вітки вниз |
-
Графік функції
|
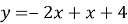
А) В (1;3) |
Б) С (0;-4) |
В) Р (4;1) |
Г) К (0;0) |
-
Яким методом найзручніше розв’язати нерівність
.
|
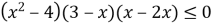А) графічно |
Б) аналітично |
В) метод інтервалів |
Г) немає правильної відповіді |
-
Знайти першу координату вершини параболи
.
|
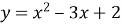А) 1,2 |
Б) 2 |
В) 3 |
Г) 1,5 |
-
Нерівність
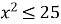має розв’язок:
|
А) |
Б) |
В) |
Г) |
-
Побудувати графік функції:
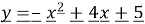. Вказати проміжки зростання і спадання функції. Вказати область значень цієї функції.
-
Розв’язати нерівность:
.
-
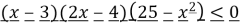При яких значеннях вираз
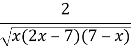має зміст ?
-
Знайдіть при яких значеннях х тричлен
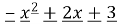набуває додатніх значень.
-
Знайдіть при яких значеннях а рівняння
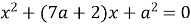має два різні корені.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
2 |
1 |
1 |
2 |
2 |
Варіант 2
-
Графік функції
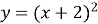зміщений ….. .
|
А) вправо |
Б) вверх |
В) вниз |
Г) вліво |
-
Графік функції
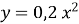є …. .
|
А) звуженим |
Б) вітки вверх |
В) розширеним |
Г) вітки вниз |
-
Графік функції
|
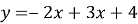
А) В (1;3) |
Б) С (0;4) |
В) Р (4;1) |
Г) К (0;0) |
-
Яким методом найзручніше розв’язати нерівність
.
|
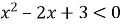А) графічно |
Б) аналітично |
В) метод інтервалів |
Г) немає правильної відповіді |
-
Знайти першу координату вершини параболи
.
|
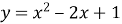А) 1,2 |
Б) 2 |
В) 3 |
Г) 1 |
-
Нерівність
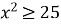має розв’язок:
|
А) |
Б) |
В) |
Г) |
-
Побудувати графік функції:
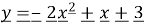. Вказати проміжки зростання і спадання функції. Вказати область значень цієї функції.
-
Розв’язати нерівность:
.
-
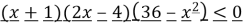При яких значеннях вираз
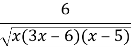має зміст ?
-
Знайдіть при яких значеннях х тричлен 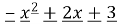набуває від’ємних значень.
-
Знайдіть при яких значеннях а рівняння
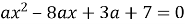не має коренів.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
0,5 |
0,5 |
0,5 |
0,5 |
1 |
1 |
2 |
1 |
1 |
2 |
2 |
про публікацію авторської розробки
Додати розробку