Узагальнюючий урок " Арифметична прогресія"

Тема: Арифметична прогресія

Мета: узагальнити і систематизувати знання учнів з теми «Арифметична                                 прогресія»; удосконалити вміння та навички розв’язувати  вправи із використанням властивостей прогресії; розглянути використання теорії послідовностей за межами алгебри;

розвивати мислення в процесі створення математичних моделей до розв’язування задач; розвивати навички спів навчання і взаємонавчання;

виховувати уважність і інтерес до пізнання предмета математики.

Тип уроку: узагальнення і систематизація знань, умінь і навичок.

Обладнання: підручник Мерзляк Аркадій Григорович, Полонський Віталій Борисович, Якір Михайло Семенович АЛГЕБРА підручник для 9 класу

загальноосвітніх навчальних закладів, ноутбук з дошкою, картки - завдання, презентація, конверти з завданням для домашньої роботи.

                                                                                               Девіз  уроку:                                                                                

                                                                               «Зібратися разом – це початок,               

                                                                                триматися разом – це прогрес,

                                                                                працювати разом – це успіх».

                                                                                (Генрі Форд,

                                                                                   американський підприємець)

Хід уроку:

І. Організаційний етап.

   Розпочалося вже століття   ХХ І

То, може, люди будуть прагнуть знати менше?

Здається вивчені вже космос і моря,

Зірок будова і уся Земля.

Чи варто зайвий раз ризикувати

Заради того, щоб нове щось взнати?

Такі питання математиків дратують,

Вони сьогодні, як завжди,

Досліджують, розв’язують, рахують.

І не бояться математики  ні труднощів,

ні перешкод, ані   тенет,

Бо знають точно, що

“Прогресіо” – це рух вперед”

 

 

 

 

 

ІІ. Мотивація навчальної діяльності.

•  Арифметична прогресія відома так давно, що неможливо впевнено сказати, хто її відкрив. Адже натуральний ряд чисел 1, 2, 3,…n - це арифметична прогресія а₁ = 1, d = 1.
•   Існує історія про те, як Карл Ґаус відкрив  формулу суми перших членів арифметичної прогресії, коли навчався у третьому класі. Щоб подовше зайняти дітей, вчитель попросив клас порахувати суму перших ста чисел — 1+2+...+99+100. Учитель був вражений, коли 9 –річний Карл через хвилину сказав: « Я вже обчислив.»Ґаус помітив, що попарні суми з протилежних кінців однакові: 1 + 100 = 101,         2 + 99 = 101 і т. д., і тому зміг відразу відповісти, що сума дорівнює 5050. Дійсно, легко бачити, що рішення зводиться до формули 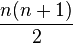, тобто до формули суми перших n чисел натурального ряду.
• Арифметичні прогресії і їх властивості вивчаються із сивої давнини. Грецьких математиків цікавив зв'язок прогресії з многокутними числами, обчислення площ і об’ємів красивими числовими співвідношеннями виду:

1 = 1²

1 + 3 = 2²

1 + 3 + 5 = 3²

1 + 3 + 5 + 7 =4².

1 = 1³

3 + 5 = 2³

7 + 9 + 11 = 3³

13 + 15 + 17 + 19 = 4³.

Отже, ми впевнилися наскільки універсальною є арифметична прогресія, тому сьогоднішній урок присвятимо саме їй.

ІІІ. Актуалізація опорних знань.

   Давайте згадаємо, що ми вивчали про арифметичну прогресію.

   Перед вами знаходяться картки – завдання, заповнимо їх.

Запитання	Відповідь	Бал
Означення арифметичної прогресії		0,5
Формула  n-го члена арифметичної прогресії		0,5
Формула суми n перших членів арифметичної прогресії		0,5
Характеристична властивість арифметичної прогресії		0,5
Властивість членів, рівновіддалених від крайніх членів прогресії		0,5

 

(Учитель пропонує учням помінятися картками і здійснити взаємоперевірку.)

ІV. Удосконалення вмінь і навичок.

Основою роботи на уроці буде метод «Ламання криги». Він полягає у тому, що кожен із вас буде подавати інформацію невідому для інших.

1. Застосування арифметичної прогресії у літературі.

Арифметична прогресія зустрічається навіть у таких предметах, які мають мало спільного з математикою, - у літературі. Наприклад,

ЯМБ – це віршований розмір з наголосом на парних складах .

 

      ХОРЕЙ – це віршований розмір з наголосом на непарних складах вірша.   

 

Усний рахунок.

Запитання:

1. Назвати перший член арифметичної прогресії.
2. Знайти різницю арифметичної прогресії.
3. Чому дорівнює дванадцятий член прогресії?
4. Чому дорівнює сума одинадцяти членів арифметичної прогресії?

 

2. Застосування арифметичної прогресії  у фізиці.

Арифметична прогресія застосовується також у фізиці. Прогресії виражають деякі фізичні явища. Наприклад,тіло, що вільно падає, рухається рівноприскорено. Відрізки шляху, пройдені цим тілом за першу, другу, третю, четверту … секунди становлять арифметичну прогресію. Також у задачах на рівномірний рух, на прискорення вільного падіння – це все є арифметичною прогресією.

 

Робота в групах.

1група.

Задача1.

   Тіло, що вільно падає, за першу секунду долає 4, 9 м, а за кожну наступну на 9,8 м більше, ніж за попередню. Знайдіть глибину шахти, якщо тіло опинилося на дні через 8 с від початку падіння.

Відповідь: 313,6 м

 

           2 група

          Задача  2.

   Гальмуючи, автомобіль за першу секунду проїхав 15 м, а за кожну наступну – на 3 м менше, ніж за попередню. Знайдіть гальмівний шлях автомобіля.

Відповідь: 45 м.

 

3. Застосування  арифметичної прогресії  у біології.

    В біології прогресії пов’язані з такими темами, як розмноження, поділ клітин, формені елементи крові та інші. Неможливо розв’язати біологічні задачі з даних тем, не використавши знання про прогресії.

   За теорією еволюції Дарвіна, всі процеси, які пов’язані з живими організмами, відбуваються прогресивно або регресивно.

    На стадії ембріона відбувається процес формування тканин, який називається гістогенез. Одним з видів сполучної тканини, яка формується на стадії формування ембріона, є кров, до складу якої входять життєво необхідні клітини – еритроцити, лейкоцити та тромбоцити, кількість яких впливає на самопочуття людини.

 

Робота біля дошки

    Задача 3.

    Кількість еритроцитів ( з розрахунку на 1 мм³) в крові людини становить на рівні моря – 5 мільйонів. Через кожні 600 м підняття в гору їх кількість збільшується на 1 мільйон. Яка кількість еритроцитів буде в крові людини, якщо вона підніметься на вершину гори Еверест (4800 м) ?

Застосуйте ваші знання з математики.

5,  6,  7,   8, …     

Вчитель:  Що це за послідовність?        (АП)

Вчитель:  Що дано?    Що знайти?

a₁=5,     d = 1,   h = 4800,    h₁ = 600,    a_n - ?        

n = 4800 : 600 = 8,       

a₈ = a₁ + 1(n – 1) = 5 + 7 = 12 (млн)     

Відповідь: 12 млн

 

4. Застосування  арифметичної прогресії  у історії.

Задачі на прогресії, які дійшли до нас із давнини, були пов’язані із господарським життям(розподіл продуктів, поділ спадщини та інше), зі спостереженнями над явищами природи.

 

Метод «Прес»

Задача 4.

Сто мір хліба слід розділити між п’ятьма чоловіками так, щоб другий одержав на стільки ж більше від першого, на скільки третій одержав більше від другого, четвертий – більше від третього і п’ятий більше від четвертого. Крім того, двоє перших повинні одержати в 7 разів менше за трьох інших. Скільки потрібно дати кожному?

 

5. Застосування  арифметичної прогресії  у алгебрі.

Вчитель: На зв'язок між  числовими послідовностями, прогресіями  та реаліями життя   першим звернув увагу великий вчений, який жив у 287 -212 роки до нашої ери,, прізвище якого ми дізнаємося трошки пізніше. А зараз попрацюємо в парах.

Робота в парах.

   Задача 5.  ( 1пара)

Знайти перший член і різницю арифметичної прогресії, якщо а₅ + а₁₃ = 38, а₄ + а₈ = 29.

Відповідь: а₁ = 7, d = 1,5.

 

Задача 6. ( 2 пара)

Чому дорівнює сума всіх від'ємних членів арифметичної прогресії :            -4,7;  -4,3;  -3,9; …?

 Відповідь:. -15

 

Задача 7. ( 3 пара)

Знайдіть суму всіх натуральних чисел, які кратні 8 і не більші за 210.

      Відповідь: 2808

Вчитель: Давайте назвемо прізвище вченого, який бачив зв'язок прогресії з життям, давши відповіді на запитання і скориставшись таблицею-ключем.

1. Скільки від'ємних членів містить арифметична прогресія в задачі    № 6? (12)
2. Чому дорівнює перший член арифметичної прогресії у задачі № 5? (7)
3. Чому дорівнює різниця арифметичної прогресії у задачі № 7? (8)
4. Чому дорівнює різниця прогресії в задачі № 5? (1,5)
5. Суму скількох членів арифметичної прогресії потрібно знайти в задачі № 7? (26)
6. Чому дорівнює сума від'ємних членів прогресії в задачі  № 6? (-15)
7. Яка відповідь у задачі № 7? (2808)

 

Х	А	Д	М	Р	Е	І
8	12	2808	26	7	-15	1,5

 

   Архімед був далекоглядною людиною і бачив, що арифметична прогресія застосовується під час розв’язування задач з життя.

Клас працює над задачею №8, а один учень над задачею № 9.

Задача 8.

   Корова за день дає 24 л молока. Після виходу на пасовище щодня додається однакова кількість молока. За тиждень, якщо корова буде пастися, то надоять 178,5 л молока. Скільки літрів молока додасть корова кожного дня?

Відповідь: 0,5 л

 

Задача 9.

Бригада за один день вирила 20 м траншеї, а за кожен наступний день на 4 м більше. Скільки метрів траншеї прорили від третього до сьомого дня?

Відповідь: 180 м.

 

V. Домашнє завдання:  на 10 - 12 б: скласти кроссенс з теми «Арифметична прогресія», завдання з конверта №5, 6;

на 7 - 9 б:  скласти кросворд, завдання з конверта № 3, 4;

на 5 - 6 б: завдання з конверта № 1, 2 .

повторити пункти 15-17 .

Завдання в конверті.

1. Знайти десятий член арифметичної прогресії 10,2; 8,2; …
2. Знайти суму перших п′яти членів арифметичної прогресії( х_n ), якщо   х₁ = 2,  d = - 3.
3. Чи є число – 32 членом арифметичної прогресії ( a_n ), у якої а₁ = - 8,      d = - 2, 4?
4. Знайдіть перший член і різницю арифметичної прогресії ( a_n ), якщо    а₁ + а₆ = - 12,6; а₅ – а₂ = - 9.
5. Знайдіть кількість додатних членів арифметичної прогресії 91; 89,5; …
6. Знайти суму перших двадцяти членів арифметичної прогресії ( a_n ), якщо а₅ = 1; S₆ = - 1,2.

VІ. Підсумки уроку.

Ми закінчили знайомство з темою «Арифметична прогресія».  Давайте спробуємо скласти ейдос-конспект з цієї теми.

 

   Ян Амос Коменский говорив: «Уважай  нещасним  той день або ту годину, у яку ти не засвоїв нічого нового, нічого не додав до свого розвитку». Я сподіваюсь, що на сьогоднішньому уроці ви знайшли для себе хоч крупинку корисного. Нехай вам щастить!