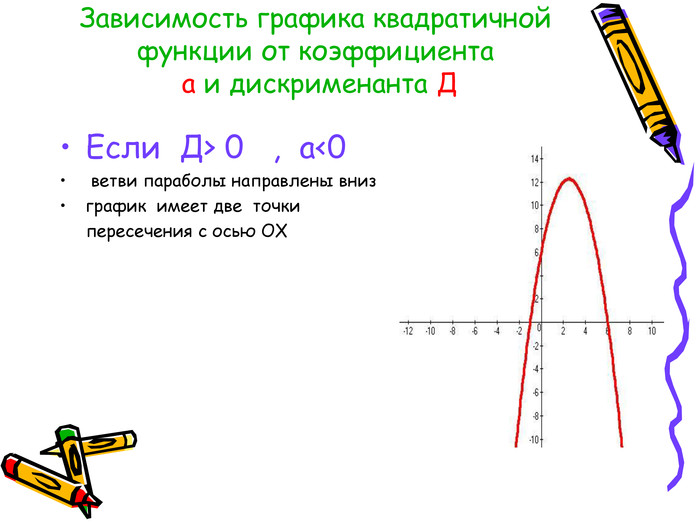
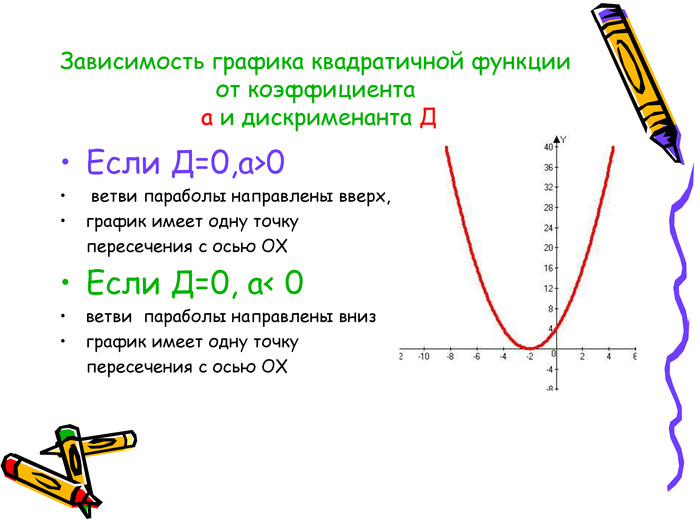
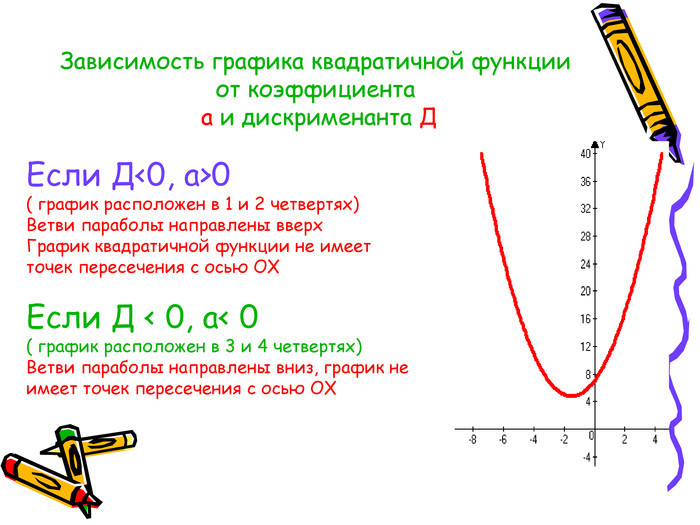
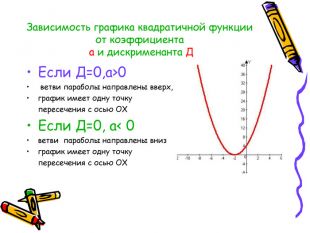
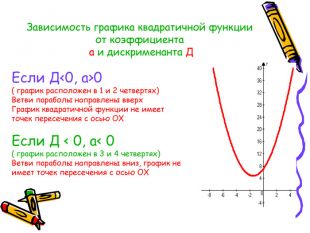
Квадратична функція та її графік
Про матеріал
Презентація к уроку алгебри для повторення тем за курс 8 класа. Дає змогу повторити відомості про квадратичну функцію. Також можно використовувати на уроках алгебри. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
Вправи для повторення курсу алгебри 8 класу Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку