Квадратична функція та їх застосування

Про матеріал

Узагальнити й систематизувати знання, вміння і навички учнів з теми «Квадратична функція»; розширити світогляд учнів щодо використання властивостей квадратичної функції в практичній діяльності людей

Перегляд файлу

9 клас

Алгебра

Тема:

«Квадратична функція та її властивості»

Олізар Ольга Михайлівна

вчитель математики

вища категорія

вчитель -методист

Літківська загальноосвітня школа І – ІІІ ст. ім. М.П. Стельмаха

9 клас. Урок узагальнення та систематизації.

(на базі класу інформаційно-комунікаційних технологій)

Використання програмних засобів на уроках математики та національно-патріотичне виховання учнів у процесі вивчення математики

Тема. Квадратична функція та її властивості.

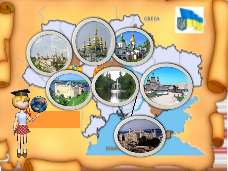
Віртуальна подорож до 7 чудес України

Мета: узагальнити й систематизувати знання, вміння і навички учнів з теми «Квадратична функція»; розширити світогляд учнів щодо використання властивостей квадратичної функції в практичній діяльності людей.

Учитель.«Сім чуде́с Украї́ни» — сім історико-культурних пам'яток України. Список складено за версією оргкомітету всеукраїнської акції Сім Чудес України 21 серпня 2007.

Актуалізація опорних знань. До вершини майстерності

І сходинка «Буква З»

Учень. Історична довідка. Функція – одне з найважливіших понять сучасної математики . Воно виникло в ХVII ст. . Поняття змінної величини і функції вперше ввів Р. Декарт . Термін функція походить від латинського слова funktio , що означає діяльність , виконання . Його ввів німецький математик Г. Лейбніц у 1694 році .

Учень. Острів Хортиця (Запоріжжя) Хо́ртиця – найбільший острів на Дніпрі, розташований у районі міста Запоріжжя нижче Дніпрогесу, унікальний природний й історичний комплекс. Хортиця є одним з Семи Чудес України.

ІІ сходинка «Буква Н»

Учитель.

Усне опитування/ Відповіді учнів

1) Яка функція називається квадратичною?

2) Що є графіком квадратичної функції?

3) Як впливає коефіцієнт а на напрям віток параболи?

4) Що таке нулі функції?

5) Охарактеризуйте графік функції y = x^2.

6) Як із графіка функції y = x^2 одержати графіки наступних функцій:

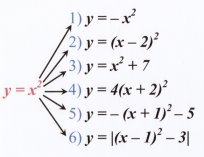
$C:\Documents and Settings\Администратор\Мои документы\Мои рисунки\MP Navigator\2008_01_11\IMG_0003.jpg$

Учень. Софія Київська (Київ) Собор святої Софії - Премудрості Божої, Софія Київська або Софійський Собор — християнський собор в центрі Києва, пам'ятка української архітектури і монументального живопису 11 — 18 століть, одна з небагатьох уцілілих споруд часів Київської Русі. Знаходиться на території Софійського монастиря i є складовою Національнoгo заповідника «Софія Київська».

ІІІ сходинка «Буква А»

Учитель.

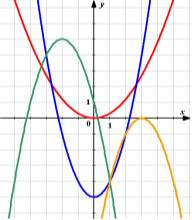
Знайдіть відповідність.

а) у = х^2 – 5 б) у = 0,3 х^2 в)у = – (х – 3)^2 г) у = – (х+ 2)^2 +5

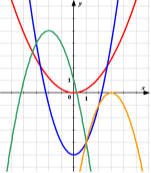
$C:\Documents and Settings\Администратор\Рабочий стол\функция разноуровневый урок\для презентации\Рисунок1.wmf$

Відповіді. Учні працюють у зошитах і один виходить до дошки і запиисує відповіді.

$C:\Documents and Settings\Администратор\Рабочий стол\функция разноуровневый урок\для презентации\Рисунок1.wmf$

А – синій

Б – червоний

В – оранжевий

Г - зелений

Учень. Софіївка (Умань) Націона́льний дендрологі́чний парк «Софі́ївка» — парк, науково-дослідний інститут Національної академії наук України.

На сьогодні — це місце відпочинку. Щорічно його відвідують близько 500 тисяч людей.

Площа — 179,2 га.

ІV сходинка «Буква Н»

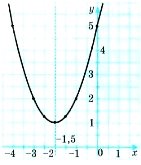
Учитель. Побудувати графік функції

у = (х+2)^2+1

Учень біля дошки будує графік функції і виконує відповідні записи.

Записати:

1. Область значень функції Е(у) є [1; ∞)

2. у > 0 х є R

3. Функція спадає при х є (-∞; - 2)

Функція зростає при х є (-2; ∞)

4. Найменше значення функції y =1

Учень. Хотинська фортеця (Хотин) Хотинська фортеця — фортеця

13 — 18 століття у місті Хотин, що у Чернівецькій області, Україна. Сьогодні на території фортеці розташований Державний історико-архітектурний заповідник

«Хотинська фортеця».

Одне з семи чудес України.

V сходинка «Буква Н»

Учитель.

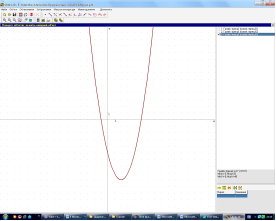
У програмі GRAND2 :

Побудувати графіки функцій

у = х^2-4х-5 (І група)

Записати:

1. Область значень функції Е(у) yє

2. у > 0 х є

у < 0 х є

3. Функція спадає при х є

Функція зростає при х є

4. Найменше значення функції

y =

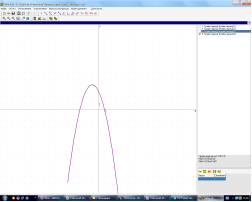
Побудувати графіки функцій

у = -х^2-2х+3 (ІІ група)

Записати:

1. Область значень функції Е(у) y є

2. у > 0 х є

у < 0 х є

3. Функція спадає при х є

Функція зростає при х є

4. Найменше значення функції

y =

Знайти значення функції у точці х=-3

у = х^2-5х+6 (ІІІ група)

Поки учні одні працюють у програмі гранд, учні зачитують:

Цікаві властивості параболи

1. Будь – яка парабола рівновіддалена від деякої точки, що називається фокусом параболи і деякої прямої, що називається її директрисою.

2. Якщо обертати параболу навколо осі то одержиться дуже цікава поверхня, яка називається параболоїдом обертання.

3. Поверхня рідини, в посудині яка обиртається має форму параболоїда обертання. Ви можете мати цю поверхню, якщо сильно помішувати ложкою в неповному стакані чай, а потім вийняти ложку.

4. Якщо в пустоті кинути камінь під деяким кутом по горизонту то він буде летіти по параболі.

Після виконнання І групи, учні міняються місцями і проводять дослідження побудованої функії, інша група виконує наступне завдання.

Наступний учень зачитує наступні Цікаві властивості параболи

1. Якщо перетнути поверхню конуса площиною паралельна якій – не будь одній його твірній, то в перетині одержимо параболу.

2. В парках культури часом влаштовують атракціони «Параболоїд чудес». Кожному хто стоїть всередині обертаючого параболоїда здається, що він стоїть на підлозі, а решта людей якимось чудом тримаються на стінах.

3. В зеркальних телескопах також застосовуються параболічні зеркала, світло далекої зірки, яке йде паралельним пучком впавши на зеркало телескопа, збирається у фокус.

4. У прожектора зеркало дуже часто робиться в формі параболоїда. Якщо джерело світла помістити в фокусі параболоїда, то промені відбившись від параболічного дзеркала утворює паралельний пучок.

Під час роботи учнів ІІІ групи, учні І та ІІ груп записують на дошці виконані завдання по дослідженню функції.

Учень. Херсонес Таврійський (Севастополь) Херсоне́с Таврі́йський - означає «півострів», за середньовіччя - Херсон, у слов'янських джерелах - Корсунь — старогрецьке місто-держава в південно-західній частині Криму (у межах Севастополя)

VІ сходинка «Буква Я»

Учитель. Два учні працює біля дошки.

Скласти рівняння траєкторії стрибка дельфіна, якщо він стрибнув на висоту 2 метра і довжина його стрибка 4 метра.

$E:\дельфины тарелка мопед\paraporpoise_lg.GIF$

Струмінь води фонтана підіймається на висоту 10 метрів і падає на відстані 6 метрів.Скласти рівняння траєкторії струменя води.

$E:\vandstrc3a5le.jpg$

у=ах^2+в

в= 2; А(-2;0) В(2;0)

ах^2+2 = у

(-2) ^2*а + 2 = 0

4а = - 2

а = - 0,5

у=-0,5х^2+2

у=ах^2+в

в= 10; А(-3;0) В(3;0)

ах^2+10 = у

(-3) ^2*а + 10 = 0

9а = - 10

а = - 10/9

у=- 10/9 х^2+10

Учень. Києво-Печерська Лавра (Київ) Свя́то-Успе́нська Ки́єво-Пече́рська ла́вра — одна з найбільших православних святинь України, визначна пам'ятка історії та архітектури.

На території Верхньої Лаври діє «Національний Києво-Печерський історико-культурний заповідник», якому було надано статус національного у 1996 році. Монастирське життя зосереджене на території Нижньої лаври. Обидві частини Лаври відкриті для відвідувачів. Києво-Печерську лавру занесено до Семи Чудес України у 2007 році за результатами голосування експертів та користувачів Інтернету.

VІІ сходинка «ВЕРШИНА»

Учень.