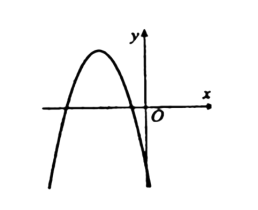Квадратна нерівність. Розв'язування квадратних нерівностей.

УРОК З АЛГЕБРИ, 9 КЛАС

Тема уроку. Квадратна нерівність. Розв'язування квадратних нерівностей.

Мета уроку: сформувати знання учнів про зміст поняття «квадратна нерівність», домогтися розуміння та засвоєння учнями схеми розв'язування квадратних нерівностей із використанням побудови графіка квадратичної функції;

розвивати логічне та критичне мислення учнів, графічні навички, просторову уяву, уміння обґрунтовувати власну позицію;

виховувати уважність, кмітливість, акуратність, самокритичність та вміння працювати в команді і в парах.

Обладнання: підручник, роздатковий матеріал, комп’ютер.

Тип уроку: засвоєння знань, формування вмінь.

ХІД УРОКУ

Організаційний етап.

Перевірка готовності учнів до уроку, налаштування на роботу.

І. АКТУАЛІЗАЦІЯ

Для актуалізації у пам’яті учнів уже наявних знань, осмислення того, що вони вже знають, учитель пропонує учням до кожного з ключових слів, використавши метод «ШВИДКЕ ПИСЬМО», дати означення, пояснення, навести приклади, якщо вони потрібні для розкриття поняття протягом 2-5 хвилин.

Ключові слова: квадратний тричлен, квадратична функція, парабола, область визначення і область значень, нерівності.

Метод «Що? – ОТЖЕ, ЩО? - ЩО ТЕПЕР?»

Учитель креслить на дошці таблицю.

Учитель пропонує  учням у колонку «Що?» підсумувати основні поняття, які вони щойно осмислювали. Записує ідеї учнів у колонку.

Запитання до учнів:

1. Що є графіком квадратичної функції?
2. Від чого залежить напрям віток параболи?
3. Які можливі випадки розміщення графіка квадратичної функції в залежності від знаку дискримінанта при а > 0?             
4.                                     Які можливі випадки розміщення графіка квадратичної функції в залежності від знаку дискримінанта при а < 0?

Виконайте завдання.

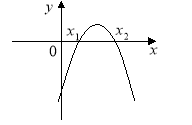
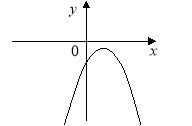
1.На рисунку зображено графік функції у = ах² +bх + c. Визначте знаки коефіцієнтів а, b і c.

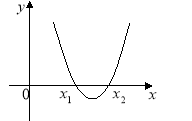
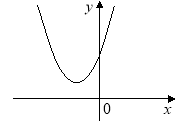
2.На рисунку зображено графік функції у = ах² +bх + c. Визначте знаки коефіцієнта a і дискримінанта D.

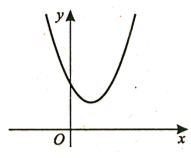
Відповідь: 3.

3.Дано вирази:

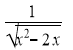1) ;  2) ;  3) .

Укажіть нерівність, яка є записом умови існування кожного з даних виразів:

а) х ≥ 0; б) х > 0; в) ≥ 0; г)  х² – 2х ≥ 0;     д) х² – 2х > 0.

Відповідь: 1-б; 2-д; 3 –г.

ІІ.  ПОБУДОВА ЗНАНЬ

Завдання: використайте схему Венна для визначення зв'язків між поняттями: квадратне рівняння, квадратична функція, нерівності.

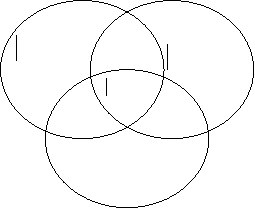Відповідь: квадратні нерівності.

Отже, що?  Подумайте, що є важливим, які знання у вас уже є з даної теми? Які кроки ви пропонуєте для вирішення цих питань?

Крок 1. Означення квадратної нерівності. Приклади квадратних нерівностей з різними коефіцієнтами.

Який зміст має зауваження а ≠ 0?

(Відповідь: якщо a = 0 нерівність не буде квадратною).

Зверніть увагу на нерівності виду ах² + с > 0,

(так само, як і квадратний тричлен, квадратна нерівність може мати «скорочений» вигляд).

Після обговорення вчитель записує узагальнені пункти до колонки        «Отже, що?».

Що тепер? Учитель запитує учнів, як вони можуть примінити свої знання до розв’язування квадратнних нерівностей? (Відповіді учнів).

• Який метод розв’язування квадратного рівняння більш наочний? (графічний)
• Яка буде наша мета? Навчитися розв’язувати квадратні нерівності за допомогою графіка квадратичної функції.

Крок 2.  Розв'язування квадратних нерівностей за допомогою побудови графіка відповідної квадратичної функції.

Метод «Читання в парах – Узагальнення в парах».

Учитель пропонує учням, використавши метод «Читання в парах – Узагальнення в парах», уважно ознайомитися з алгоритмом розв'язування квадратних нерівностей.

Нагадує учням про необхідність мінятися ролями після обговорення кожного пункту.

  Крок 3.

Розв’язати нерівність:  х²+4х+5 > 0.

Розв’язання

у = х²+4х+5 - квадратична функція, графіком є парабола, вітки якої напрямлені вгору ( а =  1 > 0);

D = - 4 < 0.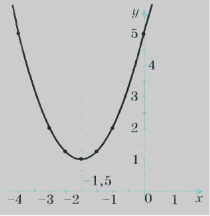

Координати вершини параболи:

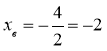
y_в=4-8+5=1;

( -2; 1 ) – вершина параболи.

х= - 2 -  вісь  параболи.

Координати ще кількох точок параболи:

х=0,  у=5 ;             (0; 5);

х= -1, у=1-4+5=2 ;  (-1; 2).

      Відповідь:  х²+4х+5 > 0 при всіх значеннях  хR.

Запитання до учнів.

• Які значення змінної х необхідно знати, щоб записати розв’язок нерівності?
• Чи обов'язково точно будувати графік функції.

Висновок. Різні способи розташування графіка квадратичної функції

 y = ax² + bx + c відносно осі Ох залежно від знака старшого коефіцієнта а та знака дискримінанта D квадратного тричлена ах² + bх + с.

Крок 4. У колонку «Що тепер?»  запишіть алгоритм розв'язування квадратних нерівностей.

АЛГОРИТМ

1. Приведіть нерівність до виду   ().

2. Розгляньте функцію  . 

3. Визначте напрям віток параболи.

4. Знайдіть точки перетину параболи з віссю абсцис (для них y = 0; знайдітьі , розв’язуючи рівняння ).

5. Схематично побудуйте графік функції  .

6. Виділіть частину параболи, для якої y > 0 (y < 0).

7. На осі абсцис виділіть ті значення х, для яких y > 0 (y < 0).

8. Запишіть відповідь у вигляді проміжків.

Розв’язування вправ

1. Виконати  № 399  (1, 9, 15 ) підручник ст.123.
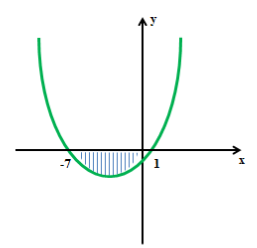
2. Розв’яжіть нерівність   х²+6х-7 < 0.

у = х²+6х-7

      Графік – парабола.

а =1 > 0 – вітки параболи направлені вгору.

D = 64  > 0.

= 1; = -7.

Схематично малюємо графік квадратичної функції.   Розв’язки нерівності  х є (-7; 1).

Відповідь:  (-7; 1).

Запитання до учнів

• Чому заштрихована саме внутрішня область між точками?

 (Відповідь: функція y < 0, тобто графік лежить нижче осі абсцис саме на цьому проміжку).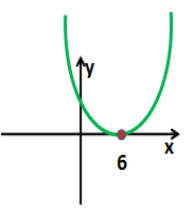

3. Розглянемо випадок, коли D = 0.

   Розв’яжіть нерівність   х²- 12х+36 ≥ 0.

у = х²- 12х+36, графік – парабола,

 а =1 > 0 – вітки параболи направлені вгору,

D =0,  == 6.  

Відповідь:  х є R.

4. Розглянемо випадок, коли D < 0.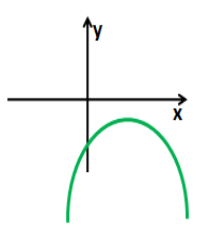 

Розв’яжіть нерівність   - 4х²+5х-7 > 0.

у = - 4х²+5х-7,  графік – парабола,

 а = - 4 < 0 – вітки параболи направлені вниз,

D = - 87 < 0,  

Відповідь:   розв’язків немає.

Прийом «ІНСЕРТ»

Учитель пропонує учням систематизувати інформацію, розташувавши її у відповідності зі своїми позначками в наступну таблицю:

«+» - я це знав;

«-» - я цього не знав;

«!» – це мене здивувало;

«?» - хотів би взнати детальніше.

ІІІ. КОНСОЛІДАЦІЯ

Самостійна работа. Одне із завдань виконує група учнів з одного ряду. Три завдання – три групи.

(Для роботи використовуються заздалегідь заготовлені таблиці з формулюванням етапів розв’язання).

Учитель контролює хід розв’язування. Після виконання завдання представники груп обмінюються виконувати дане завдання.

Підсумок. Запитання до учнів:

-  Що нового ви дізналися на уроці?

- Яку мету ставили?

- Які отримали результати?

- Де можна застосувати нові знання?

- Над чим ще треба попрацювати?

Домашнє завдання

Учням пропонується прочитати матеріал підручника § 2 п.12 (стор.119).

Вивчити означення квадратної нерівності, схему її розв'язування.

Виконати № 400 (1,4.8,9), 402.