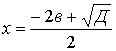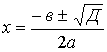Крутоярівський загальноосвітній навчально-виховний комплекс

 

 

 

 

 

 

 

 

 

 

 

 

Відкритий урок

на тему

«Квадратні рівняння»

 

 

 

 

 

 

 

 

 

 

 

                                        Підготувала

                                                       Вчитель математики

                                          Воронова А.І.

                                                    

 

 

 

 

 

 

Тема уроку: Узагальнюючий урок з теми «Квадратні рівняння»

Мета уроку: закріпити практичні та теоретичні знання і вміння учнів при виконанні завдань з теми «Квадратні рівняння»;
Розвивати самостійність, активність, увагу;
Виховувати інтерес до предмету.

Обладнання: мультимедійне обладнання, на кожній парті “Путьовий листок”, зірочки, таблиці з цифрами.
 

 

Хід уроку

І. Організаційний момент.

  1. Хвилинка емоційного настрою на урок: «Злови позитив».

Учням пропонується назвати слово - побажання усім присутнім на уроці і «передати» його рукостисканням ланцюжком (наприклад: увагу, успіх, вдалого виконання завдань, взаємодопомоги…)

     Я бажаю вам тільки позитивних оцінок і емоцій від нашого уроку і пам’ятайте: у всьому можна знайти («зловити») позитив.

 ІI. Повідомлення теми і мети уроку.

1. Зверніть увагу на епіграф до нашого уроку:

   Епіграф до уроку: (написаний на дошці)

 «Рівняння являє собою найбільш серйозну і важливу річ у математиці…»                                           

 О. Лодж

                                                                                                               

Чи згодні ви з його автором? Аргументуйте стисло (бажано прикладом) свою точку зору.(2-3 учня)

- Тож сьогодні на уроці ми з вами повторимо і узагальнимо вивчений матеріал про квадратні рівняння і їх застосування у розв’язанні задач.

Правила, якими ми будемо користуватися сьогодні на уроці

    Квадратні рівняння – це фундаментальне поняття алгебри. Квадратне рівняння знаходить широке використання при розв’язуванні тригонометричних, логарифмичних показникових  рівнянь та нерівностей (з ними ви познайомитесь у старших класах). Ви знаєте формули коренів квадратних рівнянь, за допомогою яких можна розв’язати будь-яке квадратне рівняння.  початку ми з вами повторимо вивчений матеріал.

ІІІ.Систематизація  та  узагальнення  знань  учнів.

- Отже, уявімо, що ми з вами в студії. Ви гравці, а я ведуча. У вас в кожного на партах лежать таблички з цифрами від 1 до 5.

1			2			3			4			5

- Отже, послухайте умови гри.
- Я буду ставити всім питання, а відповідно піднімати табличку з тим номером, який відповідає правильній відповіді. А так ж у кожного з вас лежать на партах листочки. За кожну правильну відповідь, коли я вам скажу, ви будете на ньому креслити зірочку. А в кінці гри ми їх підрахуємо і оцінимо роботу кожного з вас.

Проведення гри.
1.  Отже, починаємо гру. Зараз ми будемо працювати з вами по 1 таблиці
Таблиця № 1

1	2	3	4	5

-Отже, зверху ви бачите номери відповідей, а під ними відповідні відповіді. Я задаю питання, ви 5 секунд, думаєте і піднімаєте таблички з правильними відповідями.
1. Який вигляд має квадратне рівняння.
2. Назвіть формули коренів квадратного рівняння.
3. Назвіть неповне квадратне рівняння.
4. Назвіть, чому дорівнює дискримінант квадратного рівняння.
-Добре з цим завданням ви впоралися добре, майже всі учні піднімали таблички з правильними відповідями. А хто помилявся, він ще раз побачив правильні формули і сподіваюся, так само довчити матеріал.
2.А тепер ми всі переходимо до другого туру.

У другому турі ми з'ясуємо знання правил з даної теми. Працювати будемо з другої таблицею.
Таблиця № 2

1	2	3	4	5
Теорема зворотна теоремі Вієта	Квадратне рівняння	Теорема Вієта	Неповна квадратне рівняння	Зведене квадратне рівняння

Я буду говорити вам правило, а ви піднімайте відповідну картку.
1) Сума коренів наведеного квадратного рівняння рівна другому коефіцієнту, взятому з протилежним знаком, а добуток коренів  вільному члену.
-Вірно, наступне питання, слухайте і піднімайте таблички.
1) Якщо в квадратному рівнянні хоча б один з коефіцієнтів в або з дорівнює нулю, то таке рівняння називається ....
-Вірно, наведіть приклад квадратного рівняння.
2) Рівняння виду , Де х змінна, а, в, с - деякі числа, причому а  = 0 називається ....
-Вірно, наведіть приклад квадратного рівняння
Наступне питання
3) Якщо числа м і n такі, що їх сума дорівнює –р, а  добуток  q, то ці числа є коренями рівняння виду
-Вірно, скажіть, скільки коренів має неповне квадратне рівняння кожного виду.
4) Як називаються повні квадратні рівняння, у яких всі три коефіцієнта відмінні від нуля і в яких перший коефіцієнт дорівнює 1.
-Добре і з цим завданням ви справились.
3. Математичний відпочинок. Історична довідка.

 Необхідність розв'язування рівнянь другої степені, в тому числі й квадратних, у стародавні часи була викликана потребою вирішувати проблеми пов'язані з поділом землі, знаходженням її площі, земельними роботами військового характеру, а також із розвитком таких наук, як математика й астрономія. Квадратні рівняння вміли вирішувати вавилоняни близько 2000 років до н.е. Серед клинописних текстів були знайдені приклади розв'язання неповних, а також часткових випадків повних квадратних рівнянь. Відомо, що їхні методи розв'язання майже збігаються із сучасними, проте невідомо, яким чином вавилоняни дійшли до цих методів: майже на всіх знайдених до цього часу клинописних текстах збереглися лиш вказівки до знаходження коренів рівнянь, але не вказано, як вони були виведені. Однак, не зважаючи на розвинутість математики у ті часи, в цих текстах немає ані найменшої згадки про від'ємні числа і про загальні методи розв'язання рівнянь.

В стародавній Греції квадратні рівняння розв'язувалися за допомогою геометричних побудов. Методи, які не пов'язувалися з геометрією, вперше наводить Діофант Александрійський у III ст. У своїх книгах «Арифметика» він наводить приклади розв'язування неповних квадратних рівнянь. Його книги з описом способів розв'язання повних квадратних рівнянь до нашого часу не збереглися.

Правило знаходження коренів рівняння, зведеного до вигляду ax² + bx = c уперше дав індійський вчений Брахмагупта.

Загальне правило розв'язання квадратних рівнянь було сформоване німецьким математиком М. Штифелем (1487 — 1567). Виводом формули загального розв'язку квадратних рівнянь займався Франсуа Вієт. Він же й вивів формули залежності коренів рівняння від коефіцієнтів у 1591 році. Після праць нідерландського математика А. Жирара (1595 — 1632), а також Декарта і Ньютона спосіб розв'язання квадратних рівнянь набув сучасного вигляду. Вієт Франсуа (1540—1603) — французький математик і юрист народився в м. Фонтеней. (слайд 7)

Здобувши юридичну освіту, спочатку був адвокатом, а згодом став радником французького короля Генріха IV. Незважаючи на велику службову завантаженість, Вієт з великим інтересом вивчав математику, присвячуючи цьому свій вільний час. Вієта по праву називають «батьком алгебри», бо завдяки його роботам вона стала наукою про алгебраїчні рівняння, в основу якої покладено символічні позначення.

Заслугою Вієта було те, що він першим почав позначати буквами не лише невідомі, а й дані величини, тобто коефіцієнти рівнянь. Це дало можливість записувати властивості рівнянь і їх коренів загальними формулами.

Відомі величини та коефіцієнти Вієт позначав приголосними буквами b, с, d, а невідомі голосними а, о, е, ...

У житті Вієта був цікавий факт. Під час війни Франції з Іспанією іспанці використовували для свого листування складний шифр, який французи ніяк не могли розгадати. Король Франції Генріх IV звернувся до Вієта з пропозицією розшифрувати іспанські листи. Після наполегливої роботи йому вдалося це зробити. Протягом двох років французи перехоплювали і прочитували таємні листи до іспанського двору. Це давало великі переваги французькому командуванню. Армія Франції завдала ряд поразок армії Іспанії. Іспанці зрозуміли причину своїх невдач і дізналися, хто розшифрував їхній тайнопис. Іспанські інквізитори, які відзначалися особливою жорстокістю, вважали, що людині не під силу розкрити таємницю їхнього шифру, і звинуватили Ф. Вієта в спілкуванні з нечистою силою. Ф. Вієта було засуджено до спалення. На щастя, Генріх IV не видав його інквізиції.

4. Робота  в  групах – метод „Карусель”.

Учні  виконують завдання  на  аркушах:

 І група: 4Х² - 8Х = 0             (0;2)

   ІІ група: 2Х² – 50 = 0 (5;-5)

 ІІІ група: 2Х²  - 18 = 0 (3;-3)

 VІ група: 5Х² + 2Х = 0 (0;-0,4)

Після  повного  оберту „каруселі”  учень-доповідач з  кожної  команди розповідає  перед  класом  про  хід  розв’язку  рівнянь.

  5. Дискримінант якого рівняння    дорівнює 25            

 1. 4x²-3x+1=0                                                     

 2.2x²-3x+2=0                                                     

                3.2x²+3x-2=0                ******                                    

 6. Розв’язування  вправ.

Самостійна робота.
-Вам в цьому турі необхідно виконати такі завдання. На дошці виписані квадратні рівняння.
1. х ² - 9х + 20 = 0.        (4;5)      

2. 25Х² - 10Х + 1 = 0       (1/5)

3. 2х ² + 2х + 112 = 0.     ( розв’язків не має)
4. 4Х² + 5Х + 1 = 0           ( -1/4; -1)
-Ви самостійно вирішуєте ці рівняння у зошиті, а потім ми перевіримо.
-Отже, я буду називати вам рівняння, а ви піднімайте картку, відповідну

правильної відповіді.
-Добре давайте перевіримо.
7. «Аварія». Знайти помилки і пояснити, чому вони були допущені.

1) x²-2x+8=0                      2).  x²+23x+17=0                                                      

    х+х=-2                              х+х=17

    х· х=8                                х· х=-23

  8. Творчі завдання.  Робота  в  парах.                                                                                                                                      

1.          Скласти  квадратне  рівняння  за  його  коренями: 2 і 7.
2.          Скласти  квадратне  рівняння  за  його  коренями: 3 і 5.

 

IV. Підсумок уроку
Отже, ось і підходить до кінця наша гра. У ході гри ми повторили теоретичний і практичний матеріал, і тепер ми можемо підвести урок гри.

Підрахуйте свої зірочки
-Хто набрав від 20 до 25 зірок отримують «10»
-Хто набрав від 20 до 15 зірок отримують «7,8,9»
-Хто набрав 15 зірок і менше отримують «5,6»

V. Домашнє завдання

1.Вивчити складені на уроці алгоритми.

2.Використовуючи алгоритми, виконати завдання домашньої кон­трольної роботи.

Домашня контрольна робота

1. Знайдіть корені рівняння:
   а) 5х² = 25х; б) 100х² – 16 = 0; в) 3х² – 11x – 4 = 0;

г) х² – 2x + 1 = 0; д) 2х² + 5х + 9 = х + 2.

2. У рівнянні х² + рх – 18 = 0 один з коренів дорівнює -9. Знайдіть дру­гий корінь і коефіцієнт р.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Гра « Доміно»

D=в2-4ас	Формула дискримінанта
D - додатне число	Рівняння має два корені
D=0	Рівняння має один корінь
D- від'ємне число	Коренів немає

 

На звороті повинен  утворитись один із висловів.

«Недостатньо знати, необхідно також застосовувати.
Анатоль Франс»

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 ЕВКЛІД

ІІІ СТ. ДО Н. Е.

 

 

 

 

 

 

 

 

 

Евклід — один з найвидатніших старогрецьких математиків. Ніяких біог­рафічних відомостей про його життя не збереглося. Відомо тільки, що на за­прошення царя Птоломея Евклід приїхав у III ст. до н. е. в м. Александрію — ре­зиденцію грецьких царів у Єгипті — і почав там працювати наглядачем славнозвісної бібліотеки. У бібліотеці зберігалися й математичні праці учених — попередників Евкліда. Проте вони були розрізненими і несистематизованими. Учений довгі роки працював над упорядкуванням математичної спадщини минулих поколінь і створив велику працю, що складалася з 13 книг і названа «Начала». Така на­зва обумовлювалася метою: викласти в стропи науковій послідовності голо­вне, основне в математичних знаннях, що є грунтом для їх практичного засто­сування.

Спочатку Евклід сформулював п'ять аксіом про ознаки рівності і нерівності величин і п'ять постулатів, тобто вимог, додержання яких дає можливість вико­нувати всі геометричні побудови. На основі цих первинних незаперечних суд­жень, які приймаються без доведення, учений будує систему теорем, які вже доводить дедуктивне.

Створивши такий дедуктивний курс геометрії, Евклід переміг величезні труд­нощі в узагальненні і доведенні багатьох складних співвідношень між елемен­тами площинних і просторових фігур, що виражаються числами. Ці труднощі посилювалися тим, що на той час ще не було створено буквеної символіки для позначення величин. У своїх працях Евклід позначав буквами точки, користу­вався рисунком, а математичні перетворення і доведення подавав писаною мовою, хоч йому доводилось часом оперувати в своїх викладках складними ірраціональними виразами, перетворювати і спрощувати їх.

Величезною заслугою Евкліда було те, що він засобами геометрії дослідив багато важливих питань арифметики і алгебри, а також створив дедуктивний курс геометрії, визначивши систему аксіом і постулатів для побудови такого курсу. «Начала» Евкліда збереглися на віки як величний пам'ятник людині, обдаро­ваність і могутній талант, дивовижна сила уяви і мислення якої залишилися не­вмирущими у скарбниці загальнолюдської світової науки і культури.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 М

 

 

 

               

 

              Мухаммед

аль-Хорезмі (783 — бл. 850)

 

 

Властивості рівнянь першим сформулював узбецький математик IX ст. Мухаммед аль-Хорезмі (Мухаммед з Хорезму). В ті далекі часи від'ємні числа не вважались справжніми. Тому коли в результаті перенесення від’ємного члена рівняння з однієї його частини в іншу цей член ста­вав додатним, вважалось, що він відновлювався, переходив з не­справжнього в справжній. Таке перетворення рівнянь Мухаммед аль-Хорезмі назвав відновленням (аль-джебр). Властивість про зни­щення однакових членів рівняння в обох частинах він назвав проти­ставленням (аль-мукабала). Книга про ці перетворення мала назву «Кітаб аль-джебр аль-мукабала»

(Книга про відновлення і протиставлення). Згодом цю книгу переклали латинською мовою, взявши для назви тільки її друге слово, яке стали писати АІ£еЬг, Звідси і пішла назва науки — алгебра. Перетворення аль-джебр стало важливим кроком у розвитку алгебри, бо наба­гато спростило розв'язування рівнянь.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ФРАНСУА  ВІЄТ

1540 - 1603

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Французький вчений, зробив великий внесок для розвитку математики, вва­жається «батьком сучасної ал­гебри»: він написав першу в світі роботу з символічної ал­гебри. Вієт ввів буквене позна­чення невідомих, саме від ньо­го бере початок сучасна алгеб­раїчна символіка. Захопив­шись якоюсь математичною задачею, він міг працювати над нею іноді три доби без їжі і сну.

Перша його наукова робота має назву «Математичний канон». Вієт був дуже відомим математиком.

В останні роки свого життя Вієт був радником французьких ко­ролів Генріха III і Генріха IV. Під час війни між Францією та Іспанією іспанці застосовували для таємного листування дуже складний шифр. Завдяки цьому Іспанія мала можливість вільно підтримувати зв’язки з су­противниками французького короля навіть у межах Франції. Після безрезультатних пошуків ключа до цього шифру король Генріх Четвертий звернувся за допомогою до Ф. Вієта. Вієт відразу відгук­нувся на це прохання. Він працював днями і ночами протягом двох тижнів, доки поставлена задача не була розв’язана. Він не тільки розгадав цей складний шифр, але і вказав спосіб, як слідкувати за всіма його змінами. Після цього Генріх IV зробив Вієта своїм осо­бистим радником.

Іспанці довгий час не могли зрозуміти причини їх невдач у військових справах. Нарешті з таємних джерел їм стало відомо, що їх шифр для французів вже не секрет і винний у його розшифровці Франсуа Вієт. За це іспанська інквізиція заочно засудила вченого до страти.