Арифметичний квадратний корінь з добутку, дробу.
Тема. Арифметичний квадратний корінь з добутку, дробу.
Мета: домогтися засвоєння учнями змісту та схеми доведення властивостей добування арифметичного квадратного кореня з добутку та відношення двох раціональних виразів; сформувати в учнів уміння відтворювати зміст вивчених властивостей, застосовувати їх для перетворення квадратного кореня з добутку (відношення виразів) у добуток (відношення квадратних коренів), а також навпаки - для перетворення добутку (відношення) квадратних коренів у квадратний корінь з добутку (відношення).
Тин уроку: засвоєння знань та вмінь.
Наочність та обладнання: опорний конспект «Арифметичний квадратний корінь та його властивості».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Щоб перевірити засвоєння учнями змісту матеріалу попереднього уроку (дійсні числа), вчитель може провести математичний диктант з наступною перевіркою.
В учнів, які потребують додаткової педагогічної уваги, вчитель збирає зошити на перевірку.
Математичний диктант
|
Варіант 1 |
Варіант 2 |
|
1. Закінчіть речення: |
|
|
Раціональне число — це число, яке можна записати у вигляді нескоротного дробу |
Будь-яке раціональне число можна записати у вигляді... |
|
2. Запишіть десятковий дріб |
|
|
2,38(742) |
30,7(384) |
|
Підкресліть період цього дробу |
|
|
3. Як називають числа,які подаються у вигляді нескінченного неперіодичного десяткового дробу? |
Запишіть будь-яке ірраціональне число |
|
4. Подайте число |
|
|
|
|
|
у вигляді періодичного дробу |
|
III. Формулювання мети і завдань уроку
З метою створення відповідної мотивації навчальної діяльності учнів можна запропонувати до розв'язання таке завдання:
Не використовуючи калькулятора та довідкового матеріалу, знайдіть значення виразів: ![]() ;
; ![]() ;
; ![]() ·
·![]() ·
·![]() .
.
Учні усвідомлюють, ідо зміст завданім полягає у необхідності обчислення значень числових виразів, які містять арифметичний квадратний корінь з добутку кількох точних квадратів, а також корінь з відношення чисел, які є точними квадратами, або добуток та відношення двох ірраціональних виразів виду ![]() . Спроба розв'язати завдання, обчисливши значення підкореневого виразу, показує учням нераціональність такого способу розв'язання (навіть якщо значення підкореневого виразу вручну обчислюється, значення кореня з такого великого числа без використання довідкових матеріалів неможливе). В останньому випадку такий порядок виконання дій взагалі неможливий: застосування одного лише означення арифметичного квадратного кореня для обчислення значення подібних до розглянутих числових виразів не дає точного значення виразу (
. Спроба розв'язати завдання, обчисливши значення підкореневого виразу, показує учням нераціональність такого способу розв'язання (навіть якщо значення підкореневого виразу вручну обчислюється, значення кореня з такого великого числа без використання довідкових матеріалів неможливе). В останньому випадку такий порядок виконання дій взагалі неможливий: застосування одного лише означення арифметичного квадратного кореня для обчислення значення подібних до розглянутих числових виразів не дає точного значення виразу (![]() ,
,![]() ,
,![]() ,
,![]() — ірраціональні числа), тому формулюється проблема: необхідно дослідити питання про існування і способи застосування властивостей арифметичного квадратного кореня, які б можна було використати для розв'язування завдань на обчислення значень числових виразів, що містять арифметичний квадратний корінь із добутку, частки, добутку коренів та частки коренів. Формулювання, доведення цих властивостей та формування первинних умінь їх застосування — це і є основною метою уроку.
— ірраціональні числа), тому формулюється проблема: необхідно дослідити питання про існування і способи застосування властивостей арифметичного квадратного кореня, які б можна було використати для розв'язування завдань на обчислення значень числових виразів, що містять арифметичний квадратний корінь із добутку, частки, добутку коренів та частки коренів. Формулювання, доведення цих властивостей та формування первинних умінь їх застосування — це і є основною метою уроку.
IV. Актуалізація опорних знань та вмінь
Для успішного сприйняття учнями навчального матеріалу уроку перед його вивченням слід активізувати такі знання учнів про властивості степеня з цілим показником (зокрема властивість про піднесення до степеня добутку та дробу); формулювання означення арифметичного квадратного кореня з невід'ємного числа та його застосування для доведення того факту, що дане число являє собою арифметичний квадратний корінь з числа; піднесення до квадрата, та навпаки, добування квадратного кореня з точних квадратів; застосування основної тотожності для квадратного кореня; розкладання раціональних чисел на множники.
Виконання усних вправ
-
Знайдіть квадрати чисел: 10; -8;
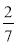 ; 0,9.
; 0,9.
-
Укажіть, які з чисел
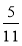 ; - 0,9;
; - 0,9; 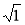 ;
; 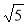 ; π;
; π; 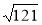 ;
; 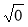 ;
; 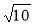 ;
; 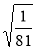 ;
; 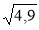 є:
є:
а) раціональними; б) ірраціональними; в) дійсними числами.
-
Обчисліть:
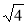 ; 2
; 2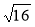 ; 0,5
; 0,5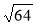 ;
; 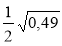 ;
; 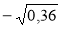 ;
; 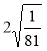 ;
; 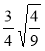 .
.
V. Засвоєння знань
План вивчення нового матеріалу
-
Формулювання і доведення тотожності
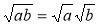 (а ≥ 0, b ≥ 0). Наслідок з неї.
(а ≥ 0, b ≥ 0). Наслідок з неї.
-
Формулювання і доведення тотожності
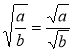 (а ≥ 0, b > 0).
(а ≥ 0, b > 0).
- Приклади застосування доведених тотожностей.
Опорними для тотожностей, винесених для вивчення на уроці, є означення арифметичного квадратного кореня з числа та основна тотожність для квадратного кореня (![]() ), зміст яких повторюється в ході виконання усних вправ.
), зміст яких повторюється в ході виконання усних вправ.
Доведення властивостей ![]() і
і 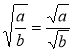 (для а ≥ 0, b ≥ 0 та для а ≥ 0 і b > 0) здійснюється за традиційною схемою:
(для а ≥ 0, b ≥ 0 та для а ≥ 0 і b > 0) здійснюється за традиційною схемою:
- доводимо існування виразів в правій та лівій частинах тотожностей та той факт, що вони набувають невід'ємних значень;
-
виходячи з того, ідо якщо два невід'ємні вирази рівні, то й їх квадрати рівні, підносимо обидві частини тотожності, що доводиться, до другого степеня, та, використовуючи тотожність
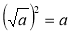 і властивість степеня (степінь добутку або степінь відношення двох виразів), робимо висновок про тотожність правої та лівої частин рівностей, які доводяться.
і властивість степеня (степінь добутку або степінь відношення двох виразів), робимо висновок про тотожність правої та лівої частин рівностей, які доводяться.
Після вивчення властивості квадратного кореня з добутку доречно буде розглянути прямий наслідок з неї, а саме добування квадратного кореня з добутку трьох і більшої кількості множників, та записати відповідну тотожність: при а ≥ 0, b ≥ 0, c ≥ 0: ![]() .
.
Після доведення названих властивостей та розгляду кількох прикладів їх застосування (зокрема див. приклад № 1 і № 2 із завдання) обов'язково слід обговорити можливість застосування доведених властивостей і в зворотному порядку: найтиповіші приклади (див. приклад № 3 із завдання — як приклад таких завдань) бажано записати в конспект як опорні.
VI. Формування вмінь
Виконання усних вправ
-
Знайдіть значення виразів:
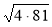 ;
; 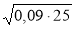 ;
; 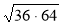 ;
; 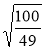 ;
; 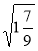 ;
; 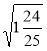 .
.
-
Кожне з наведених чисел піднесіть до квадрата:
3; -3;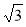 ;
; 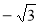 ; 2
; 2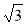 ; 3
; 3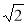 .
.
-
Подайте число у вигляді добутку найбільшого можливого точного
квадрата та іншого числа.
8; 32; 48; 50; 72.
- Розв'яжіть рівняння:
х2 = 81; х2 + 16 = 0; х2 – 7 = 0; (х – 1)2 = 3; х2 – ![]() = 0; х2 = 1; (x – 1)2 = 0.
= 0; х2 = 1; (x – 1)2 = 0.
Виконання письмових вправ
Для реалізації дидактичної мети на цьому уроці слід розв'язати завдання такого змісту:
- Знаходження значень виразів, що містять корені з добутку або частки точних квадратів.
1) Знайдіть значення виразу:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() ; д)
; д) ![]() ;
;
є) ![]() ; ж)
; ж) ![]() ; з)
; з) ![]() ; и)
; и) ![]() .
.
2) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
- Знаходження значень виразів, що містять добуток коренів або частки коренів, які потребують застосування вивчених властивостей у зворотному порядку.
1) Знайдіть значення виразу: а) ![]() ·
·![]() ; б)
; б) ![]() ·
·![]() ; в)
; в) ![]() ·
·![]() ;
;
г) ![]() ·
·![]() ; д)
; д) ![]() ·
·![]() ; є)
; є) ![]() ·
·![]() .
.
2) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) 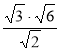 .
.
- Знаходження значень виразів, що мають вигляд кореня з різниці квадратів.
1) Обчисліть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) ![]() ; є)
; є) ![]() .
.
2) Знайдіть значення виразу: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
-
Логічні вправи та завдання підвищеного рівня складності для учнів,
які мають достатній та високий рівні знань.
1) Знайдіть значення кореня:
а) 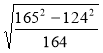 ; б)
; б) 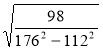 ; в)
; в) 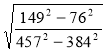 ; г)
; г) 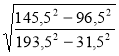 .
.
2) Відомо, що а < 0 і b < 0. Подайте вираз:
а) ![]() у вигляді добутку коренів; б)
у вигляді добутку коренів; б) ![]() у вигляді частки коренів.
у вигляді частки коренів.
3) Знайдіть пропущене число:
|
|
|
4а2b |
|
|
|
? |
-
На повторення: розв'язати рівняння виду х2 = a, а також рівняння виду
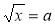 та такі, що зводяться до них шляхом рівносильних перетворень.
та такі, що зводяться до них шляхом рівносильних перетворень.
У ході виконання учнями як усних, так і письмових вправ слід вимагати від них точного відтворення формулювань властивостей, які доводяться, що сприяє прискоренню їхнього засвоєння, а також свідомому застосуванню (зокрема важливо робити акцент на факті існування виразів, що містять арифметичний квадратний корінь з числа).
VII. Підсумки уроку
В якому з випадків правильно виконано дію?
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
VIII. Домашнє завдання
- Вивчити формулювання і схему доведення властивостей:
![]() (а ≥ 0, b ≥ 0),
(а ≥ 0, b ≥ 0),
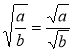 (а ≥ 0, b > 0).
(а ≥ 0, b > 0).
- Розв'язати вправи на застосування вивчених властивостей.
- На повторення: розв'язування рівнянь х2 = а та найпростіших ірраціональних рівнянь, а також рівнянь, то до них зводяться.


про публікацію авторської розробки
Додати розробку
