Рівняння, що зводяться до квадратних
Тема. Рівняння, що зводяться до квадратних
Мета: домогтися засвоєння учнями основних видів рівнянь, розв'язання яких зводиться до розв'язування квадратних рівнянь та схем їх розв'язання (дробово-раціональних рівнянь); сформувати вміння виділяти вивчені види рівнянь серед інших рівнянь, а також використовувати схеми для розв'язування названих видів рівнянь.
Тип уроку: застосування знань та вмінь.
Наочність та обладнання: опорний конспект «Рівняння, що зводяться до квадратних».
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
У разі необхідності вчитель організує роботу учнів з перевірки домашнього завдання за зразком.
III. Формулювання мети і завдань уроку
Вчитель наголошує на тому, що розглянуті на попередньому уроці рівняння не представляють усіх видів рівнянь, які розв'язуються зведенням до квадратного рівняння. Тому на цьому уроці учні мають навчитися розв'язувати ще один вид рівнянь, що зводяться до квадратних, — дробово-раціональні рівняння. Оволодіння способами дій, що передбачають зведення дробових рівнянь до квадратних, та відпрацювання вмінь виконувати дії, вивчені на попередньому уроці, — основна мета уроку.
IV. Актуалізація опорних знань та вмінь
З метою успішного сприйняття учнями навчального матеріалу уроку слід активізувати такі знання і вміння учнів: застосування загальних понять, пов'язаних із раціональними виразами (класифікація виразів, знаходження ОДЗ раціонального виразу); виконання арифметичних дій з раціональними виразами; застосування різних способів та прийомів розв'язання квадратних рівнянь різних видів; застосування вивченої схеми розв'язання дробово-раціональних рівнянь.
Виконання усних вправ
-
Знайдіть спільний знаменник для дробів:
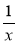 і
і 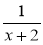 ;
; 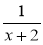 і
і 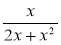 ;
;
![]() і
і ![]() ;
; ![]() і
і ![]() ;
; ![]() і
і 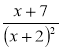 .
.
-
Спростіть вираз: а)
 ; б)
; б) 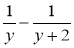 .
.
- Виконайте множення:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
-
При яких значеннях а не має змісту вираз:
а)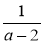 ; б)
; б) 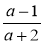 ; в)
; в) 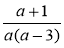 ?
?
V. Застосування знань
План вивчення нового матеріалу
- Повторення: яке рівняння називається дробово-раціональним? Чим відрізняється дробово-раціональне рівняння від цілого?
- Схема розв'язання дробово-раціонального рівняння загального виду, що зводиться до квадратного.
Вивчення питання про схему розв'язання дробово-раціонального рівняння (ДРР), що зводиться до квадратного, починається з повторення змісту понять, вивчених у темі «Раціональні вирази»: цілого, дробового і раціонального рівняння, ОДЗ рівняння, схем розв'язання ДРР (дробово-раціональних рівнянь) різних видів. Далі ці знання поширюються на ті рівняння, що зводяться до квадратних. У вивченні схеми розв'язання дробових рівнянь, що зводяться до квадратних, учителеві слід зробити акцент на тому, що схема, розглянута раніше (знайти ОДЗ даного рівняння → перейти від нього до цілого, серед коренів якого обов'язково є корені даного рівняння → позбутися сторонніх коренів, виконавши їх перевірку на відповідність ОДЗ даного рівняння), працює і в новому випадку. Так само можуть бути застосовані інші, вивчені раніше, прийоми переходу до цілого рівняння від даного дробового.
VI. Формування вмінь
Виконання усних вправ
- При якому значенні х значення дробів рівні:
а) ![]() і
і ![]() ; б)
; б) ![]() і
і ![]() ; в)
; в) ![]() і
і ![]() ; г)
; г) ![]() і
і ![]() ?
?
-
Чи може бути число х коренем рівняння
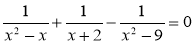 , якщо:
, якщо:
а) х = 0; б) х = 1; в) х = -1; г) х = 2; д) х = -3?
Виконання письмових вправ
Для реалізації дидактичної мети уроку слід розв'язати завдання такого змісту:
- Розв'язування ДРР (різного рівня складності).
1) Розв'яжіть рівняння:
а) ![]() ; б)
; б) 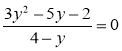 ; в)
; в) ![]() ;
;
г) ![]() ; д)
; д) 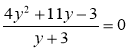 ; є)
; є) ![]() .
.
2) Розв'яжіть рівняння:
а) ![]() ; б)
; б) ![]() ; в)
; в)  .
.
3) Розв'яжіть рівняння: а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() .
.
4) Розв'яжіть рівняння:
а)![]() ; б)
; б)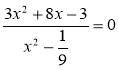 ; в)
; в)![]() ; г)
; г)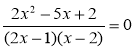 .
.
5) Розв'яжіть рівняння:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
6) Розв'яжіть рівняння:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() .
.
- Розв'язування біквадратних рівнянь (різного рівня складності).
1) Розв'яжіть рівняння:
а) х4 – 5х2 + 4 = 0; б) х4 – 7х2 – 18 = 0; в) х4 + х2 – 6 = 0.
2) Розв'яжіть рівняння: а) х4 – 3х2 + 2 = 0; б) х4 – 8х2 – 9 = 0.
-
На повторення: рівняння, що розв'язуються розкладанням на
множники.
Розв'яжіть рівняння: а) (х – 4)2 – 36 = 0; б) (2х + 3)2 – 25 = 0.
-
Рівняння виду
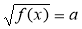 , де f(х) — або квадратний тричлен, або вираз, що зводиться до квадратного тричлена введенням нової змінної. Розв'яжіть рівняння
, де f(х) — або квадратний тричлен, або вираз, що зводиться до квадратного тричлена введенням нової змінної. Розв'яжіть рівняння 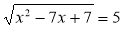 .
.
- Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.
1) Знайдіть координати точок перетину з віссю х графіка функції, яку задано формулою:
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
2) Розв'яжіть рівняння:
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]() ;
;
д) ![]() ; є)
; є) ![]() ;
;
ж) ![]() ;
;
з) ![]() .
.
3) Знайдіть корені рівняння:
а) 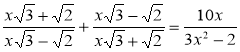 ; б)
; б) 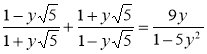 .
.
4) Знайдіть пропущений вираз:
|
х2 – 6х + 8 |
х2 + 4х – 12 |
|
|
а9b |
ab8 |
? |
- На повторення: розв'язати задачу на рух складанням лінійного рівняння.
Оскільки вивчено кілька схем розв'язання ДРР, то у ході виконання письмових вправ слід вимагати від учнів перед проведенням записів спочатку усно проаналізувати вид рівняння, а вже потім, визначившись із видом рівняння, розв'язувати його за вибраною схемою.
VII. Підсумки уроку
Самостійна робота 14
|
Варіант 1 |
Варіант 2 |
|
Розв'яжіть рівняння: |
|
|
а) х4 – 13x2 + 36 = 0; |
а) х4 – 5х2 + 4 = 0; |
|
б) (y2 + 4y – 1)(y2 + 4у + 3) = 12; |
б)(у2 – 3у – 5)(у2 – 3у + 1) = -5; |
|
в) |
в) |
|
г) (х + 3)(х – 2)(х – 4)(х – 9) = 36 |
г) (х + 4)2(х – 4)(х – 2) = -63 |
VIII. Домашнє завдання
- Повторити вивчені на уроках схеми розв'язання рівнянь, що зводяться до квадратних.
- Розв'язати вправи на застосування вивчених схем.
- На повторення: розв'язати задачу на рух складанням лінійного рівняння.
(Як варіант домашнього завдання - домашня самостійна робота.)
-
Дякую за змістовний урок


про публікацію авторської розробки
Додати розробку
