Должно быть, многие из вас не раз приходили в отчаяние на многолетнем пути обучения по математике: то никак не поймешь доказательство теоремы, вывод формулы, то задача никак не "решается", то еще какая-либо трудность.

Действительно, учиться математике нелегко. Русский писатель прошлого века Д. И. Писарев (1840-1868) даже утверждал, что "математика всегда... остается для учеников трудной работой". Несомненно, математика требует большого труда, ибо ее нельзя изучить, только наблюдая за тем, как это делают другие. Надо самому много и ежедневно работать над изучением математики, и только тогда она принесет и пользу и большую радость, радость от преодоления трудностей, радость познания. Известный педагог В. А. Сухомлинский (1918-1970) по этому поводу писал: "Ребенок, никогда не познавший радости труда в учении, не переживший гордости от того, что трудности преодолены,- это несчастный человек".

Так давайте будем счастливыми, будем переживать радость в учении, гордость за свои успехи!

Что для этого надо? Надо научиться учиться математике!

Все трудности, связанные с усвоением математики, происходят главным образом оттого, что многие из вас не умеют рационально учиться, разумно организовать свою работу. Для того чтобы учиться весело, легко и с наибольшей пользой для себя, надо овладеть техникой учения. Великий преобразователь природы И. В. Мичурин (1855-1935) писал: "Кто не владеет техникой какого-нибудь искусства, науки или ремесла, тот никогда не будет способен создать что-нибудь выдающееся".

От чего же зависит успешность овладения этой техникой?

Весьма часто малые успехи в изучении математики пытаются объяснить отсутствием способности к математике. Вот, например, какой разговор произошел между учительницей математики Марией Львовной и учащимся Сергеем после урока, на котором писали контрольную работу.

- Опять неудача? - сочувственно спросила М. Л.

- А! - махнул рукой Сергей.

- Что, формулу какую-нибудь забыл? - поинтересовалась М. Л.

- Если бы! Пример не сделал.

- Почему?

- Не догадался, как доказать тождество.

- А почему не догадался? - допытывалась М. Л.

- Ну, не сообразил,- тяжело вздохнул Сергей.

- Что значит не сообразил? Почему не сообразил?

- Ну, не сообразил, не додумался. А почему?.. Потому что плохо проанализировал тождество.

- А что надо сделать, чтобы правильно проанализировать?

Сергей осторожно и внимательно посмотрел на учительницу: не смеется ли она над ним. Но Мария Львовна была абсолютно серьезна.

- Почему ты как удивленно смотришь на меня? Ведь если я тебя спрошу, что надо сделать для отыскания неисправности в электроплитке, то ты мне, вероятно, опишешь все свои действия.

- Так то в плитке. Там понятно: или контакты где-то нарушены и надо их проверить, или провод переломан внутри, или спираль перегорела. Значит, нужно проверить вилку, контакт шнура со спиралью, посмотреть, цела ли сама спираль, и, наконец, узнать, нет ли обрыва в проводе.

- Совершенно верно. Вот ты проанализировал причины неисправности электроплитки и перечислил, какие действия надо осуществлять. А какие действия надо выполнить при анализе и доказательстве тождества?

- Так тут куда труднее. Тут математика, тут думать надо,- мрачно ответил Сергей.

- А разве в случае с плиткой ты не думал?

- Думал, конечно. Но здесь все понятно - плитка. А к математике у меня нет абсолютно никаких способностей.

- Так не бывает. Способности, в том числе и математические, есть у каждого человека. Они неодинаковые, конечно: у одних - лучше, у других - хуже. Но все зависит от хозяина этих способностей: как он ими распоряжается, как он их развивает.

- Сомневаюсь. Вот у моей сестрички, безусловно, талант к математике. Она эти задачи, как говорится, "щелкает, как орешки". А я даже не знаю, как к задаче подойти.

- Так, выходит, что родители тебя обидели? Сестренке они передали "математические гены", а тебе нет? Смешно! И потом, чтобы рассуждать, есть ли у тебя способности к математике, технике, учебе, труду и т. д., надо знать, что такое способности, из чего они складываются...

- Ну, этого никто не знает,- сказал Сергей.

- Почему же никто не знает? Знает. Есть специальная наука - психология, которая как раз и изучает, что такое способности и как их развивать. Кому и что надо делать, чтобы сформировать у себя те или иные способности? Что значит анализировать, думать? Как этому научиться? И вообще что значит учиться? И как научиться?

- Но ведь все говорят, что математические способности проявляются очень рано. Учительница Надежда Петровна рассказывала, что великий немецкий математик Гаусс заявил, будто считать он научился раньше, чем говорить. Это я понимаю: способный!

- Если ты хочешь примеры, то пожалуйста. Известного изобретателя Эдисона выгнали из школы как абсолютно неспособного ученика. Или вот, когда у отца Карла Линнея - впоследствии выдающегося биолога - спрашивали, кем будет его сын, то он печально констатировал, что способностей у его сына хватит лишь на то, чтобы научиться шить сапоги. У великого химика Менделеева частенько в школе случались большие нелады с химией. А наш знаменитый математик Лузин не мог в школе одолеть математику без репетитора... Достаточно? Или еще приводить примеры?

- Ну, это случайности. Просто у этих людей способности были, но не сразу проявились,- пытался настаивать на своем Сергей.

- Нет, дело не в случайности. Конечно, не всякий человек может стать ученым-математиком. Но ведь мы с тобой говорим не об этом, а об изучении математики: способен ли каждый изучить школьный курс математики? А на этот вопрос психология дает вполне определенный ответ: да, каждый ученик вполне способен овладеть школьным курсом математики, и если у некоторых учащихся, вроде тебя, способности к изучению математики пока еще недостаточно развиты, то это не значит, что их нельзя развить. Вот твоя сестренка, как ты говоришь, легко решает задачки. А ты думал - почему это так? Почему у нее все задачки легко решаются? Присмотрись к ней, и ты увидишь, что она любит решать задачи, что она внимательно их изучает, что она овладела секретами учения, секретами решения задач. Вот и тебе надо овладеть этими секретами, тогда ты полюбишь решать задачи и обнаружишь, что у тебя достаточно способностей для их решения.

На этом закончился разговор Марии Львовны с учеником.

Вот для того чтобы помочь ученикам, подобным Сергею, и написана эта книга. Она предназначена для тех, кто хочет быть настоящим человеком, для тех, кто стремится овладеть знаниями по математике и рациональной техникой ее изучения. В ней подробно показано: как работать в классе на уроках математики и как работать дома над выполнением домашних заданий, учить определения, правила, формулы и теоремы и как доказывать теоремы и решать задачи.

Для того чтобы наиболее успешно учиться математике, надо иметь хорошую память, устойчивое внимание, развитое воображение, логическое мышление, сообразительность и ряд других качеств, надо иметь достаточные способности для учения. Но все эти качества и способности вы можете и должны развивать у себя. В книге вы найдете указания, как это сделать, как тренировать себя, чтобы развить свою память, внимание, сообразительность и т. д. Помните призыв Карла Маркса: "Призвание, назначение, задача всякого человека - всесторонне развивать свои способности!"

Эта книга предназначена не только для тех школьников, которые хотят, но почему-то не могут подружиться с математикой - царицей всех наук. Она будет полезна и тем школьникам, которые любят эту увлекательную науку, легко и с удовольствием решают математические задачи. Они смогут узнать, правильно ли они усваивают математические понятия, проверить себя, усвоили ли они глубоко то или иное понятие, ту или иную теорему и т. д.

В первом разделе книги вы узнаете, зачем надо учиться математике, каждому ли современному человеку она необходима и почему, что значит знать и изучать эту науку. Здесь будет рассказано не только о прикладных и практических возможностях математики, но и ее роли в психологическом развитии человека: в развитии его мышления, пространственного воображения, памяти, внимания, воли и т. д. Математика - это и могучий инструмент познания окружающего мира, и, как утверждал Михаил Иванович Калинин (1875-1946) - выдающийся советский государственный и партийный деятель, очень полезная и нужная "гимнастика ума". Позже он вспоминал: "В период своей юности я любил заниматься и математикой. Каждый вечер, как ложиться спать, я решал одну- две задачи по геометрии, алгебре или арифметике".

Во втором разделе книги рассмотрены основные объекты, с которыми вы встречались в процессе изучения математики (понятия, их определения, классификация; математические предложения, их виды и т. д.). Вы, тем самым, узнаете, чему надо учиться в математике, какими действиями надо овладеть.

Третий раздел посвящен самому сложному вопросу: как изучать математику в зависимости от того, где и когда это изучение происходит (в классе или дома, по учебнику или при объяснении учителя, самостоятельно или коллективно и т. д.). Здесь анализируются формы работы с математическим материалом, указывается, в чем должна состоять самостоятельная работа над этим материалом.

Наконец, последний раздел книги поможет вам установить, какими качествами к обучению математики вы уже обладаете, а какими еще нет, и, исходя из этого, определить, что именно необходимо развивать у себя в первую очередь. Не менее важен и интересен для каждого из вас вопрос о потенциальных возможностях, т. е. о том, на что вы будете способны, если достаточно потренируетесь. Это можно будет в некоторой степени определить, прорешав задачи из данного раздела.

Книга снабжена указаниями, ответами, а в некоторых случаях и полными решениями для большинства заданий и задач, помещенных во всех разделах книги. О том, как ими пользоваться, мы поговорим в свое время.

Эта книга - не для обычного чтения. С ней надо работать, имея бумагу и карандаши, притом не спеша, а внимательно вчитываясь и аккуратно выполняя все задания. Только тогда она принесет вам пользу. Если же при чтении или выполнении заданий вы встретите такие затруднения, которые самостоятельно не сумеете преодолеть, то обратитесь за консультацией к учителю.

Всем вам необходимо помнить, что наша Коммунистическая партия нацеливает на то, чтобы прививать школьнику привычку и любовь к полезному труду. Это может быть труд физический или умственный, но обязательно настоящий труд - производительный, нужный обществу.

В конце книги помещен краткий словарь основных терминов. Так что если вы встретите при чтении книги какой-либо термин, вам недостаточно понятный, то загляните в словарь.

Желаю вам успехов в овладении техникой учебного труда, в развитии своих способностей! Желаю вам успехов и радости в изучении математики!

Беседа 2. Без математики ни шагу

Как мы установили в первой беседе, математика является тем инструментом, без которого в настоящее время невозможно полноценное развитие никакой науки, с помощью которого наиболее эффективно производятся многочисленные исследования во многих науках. Следовательно, изучение какой-либо науки требует глубокого знания математики. Если же учесть, что все современное производство, сельское хозяйство, сфера обслуживания строятся на научной основе, то станет понятным следующее утверждение академика А. Н. Колмогорова: "Без знания математики нельзя понять ни основ современной техники, ни того, как ученые изучают природные и социальные явления".

Действительно, вспомните, с чем вы встречались на уроках физики, химии, географии, истории и по другим предметам? Вы встречались с разного рода формулами, вычислениями разных величин, датами, схемами, таблицами, диаграммами и т. д. А ведь все это математика. Значит, изучение почти любого предмета в школе предполагает хорошее знание математики, и без нее вы не можете освоить эти предметы.

Может показаться, что на уроках музыки, пения, рисования, физкультуры, труда математика не нужна. Но это опять-таки неверно. И на этих уроках вы все время встречаетесь с разного рода измерениями и вычислениями, например имеете дело с ритмом (а ведь законы ритма изучает математика), с перспективой (а это тоже математика) и т. д. Так что в школе вы действительно ни шагу не можете сделать без математики.

Но не только в школе. Разве в обыденной повседневной жизни вы можете обойтись без математики? Нет, конечно. И здесь вы часто встречаетесь с разного рода расчетами, измерениями, просто даже не замечая этого. Без математики вы не обходитесь ни один день.

В народном хозяйстве в настоящее время имеется более 6 тысяч профессий, владение которыми требует хорошего знания математики, устойчивых навыков ее использования. И с каждым годом число таких специальностей растет. Поэтому без настойчивого изучения математических законов нельзя стать хорошим специалистом.

Вот Сергей собирается поступать после восьмилетки в ПТУ. Будет ли он учиться на токаря, слесаря, механика, шофера или строителя, всюду ему понадобится умение читать технические чертежи, производить разного рода расчеты, вычисления. Значит, без математики ему не обойтись. И к этому он должен себя готовить, пока учится в школе.

Применение математики в производстве приносит поразительные результаты. Как-то королева Англии пригласила к себе великого Ньютона. Она попросила его сходить на ее монетный двор и подсчитать, сколько дополнительных помещений, станков и рабочих надо добавить там, чтобы выпускать в 1,5 раза больше монет. Ньютон провел полдня на монетном дворе, вникая, в производство. Остальное время суток он находился за письменным столом, занимаясь расчетами, а утром предложил королеве такое решение: можно, не добавляя ни одного нового помещения, станка и рабочего, увеличить выпуск монет в два раза. Для этого достаточно произвести лишь некоторое изменение в организации производства: изменить последовательность операций, переставить станки, по-иному использовать станки и распределение работ и др.

Задача, подобная той, которую решил Ньютон, сейчас имеет массовый характер: как рациональнее организовать перевозку грузов, как раскроить материал, чтобы было меньше отходов, как получить максимальную прибыль из данного производства и т. д. За разработку общего метода решения подобных задач наш советский математик академик Л. В. Канторович стал лауреатом Нобелевской премии.

Беседа 3. Математика ум в порядок приводит

Слова "Математика ум в порядок приводит" принадлежат великому М. В. Ломоносову (1711 -1765). Что он имел в виду?

Дело в том, что наше мышление, перерабатывая ощущения, восприятия и представления о предметах и явлениях, как бы предвосхищает будущее, указывает нам, как поступить, что сделать в создавшейся ситуации. Поэтому от того, как "работает" наше мышление, зависит, поступим ли мы правильно и разумно или нет.

Человек рождается без умения мыслить, лишь с задатками к нему. Мыслить он научается постепенно в процессе жизненной практики, в общении со взрослыми и своими сверстниками, и особенно в обучении.

Одним из наиболее важных качеств мышления является его логичность т. е. способность делать из правильных посылок (суждений, утверждений)правильные выводы, находить правильные следствия из имеющихся фактов.

О человеке, у которого хорошо развито логическое мышление, говорят, что он основательно мыслит, дисциплинированно рассуждает. Такой человек, как правило, не допускает ошибок в своих рассуждениях и выводах. Хорошо развитое логическое мышление предостерегает человека от промахов и ошибок в практической деятельности. И вот оказывается, что это ценнейшее качество возникает и развивается главным образом в процессе изучения математики, ибо математика - это практическая логика, в ней каждое новое положение получается с помощью строго обоснованных рассуждений на основе ранее известных положений, т. е. строго доказывается. Ломоносов приведенными выше словами и имел все это в виду. На это же значение изучения математики указывал М. И. Калинин, призывая молодежь серьезно изучать математику: "Математика дисциплинирует ум, приучает к логическому мышлению. Недаром говорят, что математика - это гимнастика ума".

В связи с этим легко понять, почему так важно самому выводить формулы, доказывать тождества и теоремы. Ведь дело не в том, чтобы вы запомнили их на всю жизнь. Возможно, что они забудутся, но останется привычка рассуждать, сохранится умение объяснять, доказывать не только другим, но и самому себе какие-то истины, укрепится умение искать и находить рациональные пути решения возникающих в жизни проблем.

Вот эту культуру, дисциплину мысли, ее последовательность и доказательность, глубину и критичность, широту и оригинальность, а также необходимую пищу для мышления - систему знаний -вам дает школа, и в частности уроки математики. Эта сторона обучения математике особенно важна в наши дни, поскольку сейчас объем необходимых для человека знаний резко и быстро возрастает, поэтому необходимо каждому научиться самостоятельно пополнять свои знания. Овладеть этими умениями вам поможет добросовестное самостоятельное изучение математики.

Изучение математики формирует не только логическое мышление, но и много других качеств человека: сообразительность, настойчивость, аккуратность, критичность и т. д.

Очень важным среди них является пространственное воображение, т. е. умение представить в уме (вообразить) какие-то предметы, фигуры и при этом увидеть их не только неподвижными, но и в изменении, т. е. представить, что произойдет, если их как-то переместить, повернуть и т. д. При изучении математики, при решении геометрических задач вам все время приходится делать это, и тем самым у вас постепенно развивается эта важная способность. Почему важная? Поясним на примерах. Токарь, получив чертеж, должен до работы представить себе образ той детали, которую ему нужно выточить. А портниха должна обладать хорошими способностями к пространственному воображению, чтобы правильно раскроить материал. Эти же умения и способности позволяют шахматисту направлять фигуры на доске, а полководцу - войска на поле боя. Художник или писатель должен уметь детально вообразить ту ситуацию, которую он хочет описать. Высокий уровень ориентировки в пространстве является необходимым условием для спортсмена, позволяющим ему овладеть своим телом. А инженер? А оператор? А космонавт?... Нет такой области человеческой деятельности, где не нужны были бы хорошие умения и способности к пространственному воображению.

Эта же способность представить в уме - вообразить - важна и для планирования своей работы, своих действий с. тем, чтобы они были наиболее разумными, рациональными и безошибочными.

Изучение математики, решение математических задач развивают, помимо пространственного воображения, и способность догадываться, угадывать заранее результат, способность разумно искать правильный путь в самых запутанных условиях. Прочтя задачу и еще не производя никаких действий, вы уже научились сразу видеть, что тот или иной способ непригоден для ее решения, а вот какой-то другой способ может быть использован.

Как видим, математику следует глубоко и серьезно изучать не только потому, что она служит основой научного познания, не только потому, что без нее нельзя сделать ни шагу в жизни, в практической деятельности на любой работе, но и потому, что процесс ее изучения способствует развитию у человека важнейших качеств и способностей.

Поэтому хотя изучение математики и требует большого и упорного труда, но оно приносит так много пользы, столь много радостей познания и преодоления трудностей, что вы никогда не пожалеете о затраченных усилиях.

Чему надо учиться в математике

Беседы Марии Львовны вызывали оживленные разговоры, споры между учениками. На переменах, по дороге домой после уроков они обсуждали услышанное, спорили. Многие ученики рассказали дома своим родным об этих беседах. Взрослые, работающие на заводах, в учреждениях, в институтах, подтвердили большую роль и значимость математики в их работе, приводили много примеров, когда крайне нужны были математические знания.

Наибольшие споры вызвало замечание Саши, хорошего ученика, увлекающегося литературой и историей, что главное, чему надо научиться в математике,- это разного рода расчетам, измерениям, а все остальное - многочисленные теоремы, определения и прочее - можно спокойно забыть. Нина пыталась переубедить Сашу, доказать, что нельзя овладеть умениями разного рода расчетов и измерений, не зная их теории, не понимая сущности математических действий и операций. Кроме того, ведь применения математики в жизни отнюдь не сводятся к одним лишь расчетам и измерениям. Математика широко используется как общий метод описания и изучения количественной стороны различных явлений и процессов.

Нину, к ее удивлению и радости, поддержал Сергей.

- Мне кажется, что важно научиться математически мыслить, т. е. обоснованно, четко, последовательно, логически правильно рассуждать. И всему этому как раз и учит математика. Я вот сам,- заявил Сергей,- когда ею занялся в последнее время по-настоящему, почувствовал, как стал совсем по-иному рассуждать, мыслить... И меня это очень радует. Но для этого, конечно, надо заниматься и овладевать не только расчетами и измерениями, но овладевать теорией, всякими, как Саша говорит, теоремами, определениями.

Однако полностью Сашу не удалось переубедить, тем более что его поддержали несколько учеников, которые по математике отставали. В конце одного из уроков Нина обратилась к учительнице.

- Мария Львовна, у нас в классе возник спор: чему надо учиться в математике? Что именно следует понять и знать, чем надо овладеть в математике? Может быть, Вы нам обо всем этом расскажете, очень просим Вас.

- Что же, вопрос важный и интересный. Давайте, как и раньше, после уроков, обсудим разные стороны этого большого и сложного вопроса.

Беседа 4. Математические объекты

Чтобы ответить на вопрос, чему учиться в математике, надо разобраться в том, что она - математика - собой представляет, в чем ее особенности, что и как она изучает и из каких элементов (объектов) она состоит. Конечно, все эти вопросы очень сложные, и мы подробно в них разобраться не сумеем, но получить хотя бы некоторое представление обо всем этом нам необходимо, ибо иначе просто невозможно решить, чему же учиться в математике.

Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений.

Представьте себе, что нужно рассчитать, сколько надо купить краски, чтобы покрасить потолок комнаты, если известно, что на окраску 1 м²уходит 120 г краски, или сколько нужно купить кафельных плиток для облицовки стены, если известно, что плитка имеет форму квадрата со стороной 15 см. Во всех этих случаях совершенно безразлично, какого цвета этот потолок или стена, из какого материала они построены и т. д. Важно лишь знать их форму и размеры. В этом случае говорят, что мы отвлекаемся (абстрагируемся) от всех свойств рассматриваемого предмета и выделяем лишь его форму и размер. В результате такого абстрагирования получаем математический объект - геометрическую фигуру.

В других случаях, кроме формы и размера, учитывают еще взаимное расположение частей фигуры.

Такие математические объекты, как числа, образуются путем выделения при рассмотрении различных совокупностей (множеств) однородных предметов таких общих свойств, как количество предметов в совокупности или их порядок следования, абстрагируясь от всех других свойств этих предметов (их неодинаковости, материала, цвета, величины и т. д.).

Вообще любые математические объекты - это результат выделения из предметов и явлений окружающего мира особых количественных и пространственных свойств и отношений и абстрагирования от всех других свойств. Следовательно, математические объекты реально не существуют, нет в окружающем нас мире геометрических точек, фигур, чисел и т. д. Все они созданы человеческим умом в процессе исторического развития людей и существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык. Поэтому говорят, что математические объекты - это идеальные объекты, отражающие (описывающие) реальные объекты.

Обратите внимание еще на одну особенность математических объектов. При их образовании мы не только отвлекаемся от многих свойств соответствующих предметов, но и приписываем им такие свойства, которыми никакие реальные предметы не обладают. Так, например, образуя такой математический объект, как прямая линия, мы в соответствующих предметах (край линейки, стола, луч света, нить и т. д.) не только абстрагируемся от всех их свойств, кроме свойства протяженности, но и приписываем такое свойство, как неограниченная протяженность в обоих направлениях, хотя никакой из указанных реальных предметов таким свойством не обладает. Точно так же никакая совокупность реальных предметов не является бесконечной, а вот множество натуральных чисел бесконечное, или никакой предмет не является бесконечно раздробленным, а вот число - размер этого предмета, мы считаем бесконечно раздробляемым, т. е. число можно делить на какое угодно большое число частей, и т. д.

Итак, математика изучает особые идеальные математические объекты, которые образуются путем сложной мыслительной деятельности людей в процессе познания количественных свойств и отношений, а также пространственных свойств и форм предметов и явлений окружающего мира.

Поэтому первое, чему надо учиться в математике,- это умению в процессе изучения каких-то предметов или явлений для решения задач по определению количественной стороны или пространственных соотношений этих предметов или явлений образовывать, создавать математические объекты.

Доклад 1. Общие правила работы по изучению математики

Учение для нас, учащихся, - это работа, труд, и совсем нелегкий.. Кто хочет по-настоящему учиться, хочет прочно и глубоко усвоить знания, овладеть умениями и навыками, тот должен работать ежедневно, работать так, как работают наши отцы и матери, передовые рабочие и колхозники.

М. И. Калинин писал: "В математике все основано на непрерывном труде, когда человек непосредственно собственными усилиями как бы поднимается по высокой лестнице обучения все выше и выше".

Однако, для того чтобы эта большая и сложная работа приносила ощутимые результаты, была наиболее эффективной, поднимала нас все выше и выше по лестнице изучения математики, надо строго выполнять ряд правил. Рассмотрим эти общие правила рациональной организации учебного труда по изучению математики.

1. Работа по изучению математики должна быть систематической, ежедневной, без каких-либо перерывов, за исключением, конечно, дней отдыха. Уроки по математике бывают ежедневно, и ежедневно мы должны прорабатывать дома изученный на уроках учебный материал, выполнять все задания учителя. Только при этом условий у нас не будет пробелов в знаниях и умениях, которые могут затруднить последующую работу. Ведь в математике все взаимосвязано и любое новое понятие, любое новое действие основано на предшествующих, ранее изученных. Почему у нас в классе до сих пор имеются слабо успевающие по математике ученики? Ведь раньше, в младших классах, они хорошо учились, успевали, а вот когда-то пропустили несколько занятий, не проработали тщательно изученный материал, не выполнили вовремя домашние работы, в результате образовался в их знаниях небольшой пробел, который они на первых порах даже не заметили, а если и заметили, то не придали этому большого значения. "Подумаешь,- рассуждали до сих пор некоторые из нас,- не знаю какую-то теорему, формулу, не понял доказательство теоремы, вывод формулы. Проживу и без этой теоремы или формулы, ничего страшного". А страшное получается потом, ибо постепенно маленький пробел в знаниях и умениях вызывает большой пробел, и этот пробел, это незнание растет как снежный ком, катящийся с горы. Потом такой ученик спохватывается, сидит не только вечерами, но и ночами над математикой, а толку мало, ибо неосвоенного материала накопилось так много, что "переварить" его уже очень и очень трудно. Поэтому ни в коем случае нельзя запускать проработку изученного учебного материала, выполнение домашних заданий.
2. Надо стремиться к тому, чтобы сразу понять все, что изучается на уроках, надо освоить все действия, все умения, которые отрабатываются на уроках. Главное, что для этого надо делать,- это быть на уроках математики активным участником. Учитель объясняет новый материал, доказывает теорему, выводит какую-то формулу. И ты должен вместе с ним заниматься этим доказательством, этим выводом. Не только наблюдать, как он это делает, а делать вместе с ним - в своей тетради или мысленно выполняя каждый шаг, обдумывая при этом, на основе чего сделан этот шаг, зачем он сделан, что он дает. Учитель опрашивает твоего товарища по пройденному материалу. И ты мысленно, про себя отвечай на все вопросы учителя, замечай все ошибки и недочеты в ответе товарища. И не молчи, а встань и скажи, что ты заметил неточность, как по-твоему надо было ответить на вопрос. Нельзя считать, что ты тем самым якобы подводишь товарища, ведь мы все делаем одно общее дело - мы учимся. Поправляя товарища, ты не только не подводишь его, а помогаешь ему в деле учения. И умный товарищ это понимает. Если ты что-то не понял в объяснении учителя или товарища, не стесняйся - сразу спрашивай, скажи, что тебе непонятно. Нельзя оставлять непонятым ни один из вопросов. В классе решают задачу, и ты должен ее решать, решать самостоятельно, а не списывать запись решения с доски. Твое решение отличается от решения на доске - что же, выясни, в чем дело, не ошибся ли ты или ты нашел другой способ решения. Какой из них лучший, какой более красивый? Сравни их и, если твой способ хуже, не огорчайся, а постарайся понять и усвоить другой, более изящный способ решения. Вообще, что бы ни делалось на уроке, ты должен быть активным участником, а не сторонним наблюдателем. Ведь все, что происходит на уроке математики,- это твое дело, это дело для тебя! Галилей говорил, что "без упорного умственного труда никто не может далеко продвинуться в математике. Но каждый, кому знакома радость познания, кто увидел красоту математики, не будет жалеть затраченных усилий". А известный чешский просветитель и педагог Ян Амос Коменский (1592-1670) писал: "Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию".
3. Надо стараться "докапываться" до главного, до общих основ изучаемого материала. Важно не только понять сущность изучаемой теоремы, ее доказательство, а установить, почему она так доказывается, как додумались, догадались найти такое доказательство. Значит, надо каждый раз пытаться понять те основные правила, те общие способы действий, которые лежат в основе изучаемого материала. Вот, например, выводим формулу корней квадратного уравнения ах²+bx+с=0. Для этого мы в левой части уравнения выделяем квадрат двучлена, а предварительно, чтобы легче это было сделать, делим все члены уравнения на а. Надо подумать, а зачем выделяют квадрат двучлена. Почему мы это делаем? А мы это делаем для того, чтобы свести решение нового уравнения, квадратного, к ранее решенным уравнениям - линейным. Если мы это поймем, то, встретив какое-то новое уравнение, например уравнение третьей или четвертой степени, мы сразу начнем искать способ сведения его к уже известным - к квадратным или линейным уравнениям. Или, например, изучаем теорему о диагоналях ромба, которые взаимно перпендикулярны. Надо задуматься, а является ли это свойство ромба характеристическим, т. е. таким, которое определяет ромб. Оказывается, что все зависит от того, как определяется ромб. Если ромб определяется как четырехугольник, все стороны которого равны, то перпендикулярность диагоналей не является характеристическим свойством, ибо имеются четырехугольники - не ромбы (трапеции и другие), у которых диагонали также взаимно перпендикулярны. Если же ромб определяется как параллелограмм, у которого две смежные стороны равны (значит, и все другие стороны равны), то это свойство уже является характеристическим, ибо из всех параллелограммов только ромб (и квадрат как частный случай ромба) обладает указанным свойством. Вот такие размышления об изучаемых понятиях очень полезны. Полезно, решая какую-либо задачу, доказывая какую-либо теорему, всегда задумываться над вопросами: а как догадались найти такое решение, такое доказательство? Сумела бы я так же додуматься до этого? Какие общие эвристические правила нужно знать, чтобы найти это решение? Иными словами, главной целью изучения математики должно быть для нас не просто запоминание тех или иных определений, теорем, формул и даже не просто владение ими, умение их использовать при решении задач (все это, конечно, нужно), а усвоение и овладение идеями и методами математической науки.
4. Надо приучить себя к постоянному самоконтролю и самооценке своей учебной работы.

Мы привыкли к тому, что нашу работу контролирует и оценивает учитель. Конечно, мы понимаем, что учитель это должен делать, ибо ведь ему надо знать, как мы усвоили учебный материал, что мы не поняли или плохо усвоили. Иначе учитель не сумеет правильно построить свою работу с нами. Он должен и оценивать нашу работу, наши успехи и недоработки с тем, чтобы выработать у нас правильное представление о себе, о результатах учения и чтобы поощрить хорошо работающих учеников и "пришпорить" нерадивых.

Но ведь мы учимся не для учителя, не для родителей, мы учимся для себя, и вся наша работа - это работа для себя! Поэтому контролировать и оценивать эту работу мы должны сами, как наиболее заинтересованные в ее результатах.

Самоконтроль и самооценку нужно проводить постоянно, по каждой проделанной работе. Решая задачу, доказывая теорему, выводя формулу, надо приучиться проверять (мысленно, про себя, а в нужных случаях и вслух) каждый свой шаг, оценивать его разумность, рациональность, т. е. проводить, как говорят, пооперационный самоконтроль и самооценку своих действий.

Это надо делать всегда, и тогда выработается очень полезная для жизни и труда привычка: обдумывать каждый свой шаг, оценивать его с точки зрения разумности и рациональности, необходимости, полезности.

Но такой текущий, повседневный самоконтроль и самооценка своей работы недостаточны. Надо приучить еще себя проводить итоговый самоконтроль и самооценку отдельных этапов учебной работы. Изучили какую-то тему, раздел и тут же надо проверить и оценить свою проделанную работу по этой теме, установить, с какими результатами ты пришел к концу изучения темы, что ты усвоил и как, а что не усвоил и почему.

Для этого я,- заявила Нина,- использую уже два года такой способ. У меня есть специальная тетрадь для итогового самоконтроля и самооценки. Веду эту тетрадь так.

Когда мы начинаем изучать новую тему, я записываю в тетрадь ее название и затем графлю на три столбца. В первом - знания и умения - я записываю те знания и умения, которые мы изучаем по мере прохождения темы. Во втором - результаты изучения - я отмечаю знания и умения из первого столбца, которыми я считаю, что уже овладела, и ставлю себе оценку за них; пустая клетка в этом столбце означает, что соответствующим этой клетке знанием или умением я еще не овладела. Наконец, в третьем столбце - вопросы - я записываю те вопросы, на которые я самостоятельно не смогла найти ответ, то, что я не поняла, с тем чтобы с этими вопросами прийти на консультацию к учителю.

Мне такая форма итогового самоконтроля и самооценки очень помогает. Должно быть, можно придумать и более разумные формы для ведения самоконтроля и самооценки.

Вот те общие правила, которые, по-моему, надо выполнять, для того чтобы наша учебная работа принесла нам наибольшую пользу. Я надеюсь, что эти рекомендации и советы помогут нам разумно организовать свою учебу по математике.

После доклада Нины завязалась оживленная беседа, в которой приняла участие учительница.

Вопрос. Когда лучше выполнять домашние задания - в тот же день, когда их задали, или в день, предшествующий проверке их выполнения?

Ответ. Лучше выполнять домашнее задание в тот же день, когда его задали. Полезно также вечером, перед очередным уроком, на котором будет проверка выполнения домашнего задания, еще раз просмотреть решение задач, и особенно теоретический материал, заданный для повторения.

Вопрос. Как лучше заниматься дома повторением учебного материала: индивидуально или коллективно с двумя-тремя товарищами?

Ответ. Повторением текущего учебного материала лучше заниматься индивидуально, а вот повторением итоговым, когда повторяется материал целой темы или раздела, можно заниматься коллективно. Но в этом случае важно, чтобы не получилось так, что один все рассказывает, а остальные лишь молча слушают. Надо, чтобы все активно участвовали в работе по повторению пройденного.

Вопрос. Если я внимательно и активно слушал объяснения учителя, все понял и записал в тетрадь, то для чего нужно еще дома этот же материал повторять, да еще не один раз?

Ответ. Во-первых, понять - это еще не значит усвоить, овладеть. А ведь наша задача не просто понять учебный материал, а усвоить его, овладеть им, уметь им свободно пользоваться. Во-вторых, установлено, что из понятых на уроке объяснений усваивается в зависимости от содержания от 25 до 85% знаний. Даже если какие-то определения, формулировки теорем, правил, тем более их доказательство заучить, то через полчаса сохраняется в памяти примерно 60% этих знаний, а уже на следующий день не более 34%, через 3 дня - 25%. Поэтому, для того чтобы по-настоящему и надолго усвоить знания, овладеть ими, нужно неоднократное их повторение, многократное их применение. Но это повторение нельзя проводить в форме простого заучивания, а нужна кропотливая работа по разбору, по осмыслению, по применению этих знаний.

Доклад 2. Режим и гигиена учебного труда

В сутках, к сожалению, всего 24 ч, из них по крайней мере 8 ч мы спим, 6 учимся в школе, час, а то и два, тратим на дорогу в школу и обратно. Остается всего лишь 8-9 ч на остальные дела. А как их много, как много надо и хочется сделать: хочется почитать книгу, сделать физзарядку, посмотреть кинокартину, телевизор, сходить к товарищу, к подруге, поиграть... А домашние обязанности: уборка квартиры, помощь маме, младшим братьям и сестрам... Кроме того, многие из нас занимаются по вечерам еще в разных кружках, секциях, школах. Это тоже отнимает 3-4 ч, правда не каждый день. А домашние уроки, а подготовка к урокам...

Как видим, бюджет нашего времени весьма напряженный, и надо разумно его использовать. Главное - не терять зря ни одного часа, ибо время беспрерывно течет и вернуть потерянное время, увы невозможно.

Для этого надо четко и вполне определенно знать цели и задачи своих действий, своей работы, занятий на каждый час, не суетиться, не быть игрушкой обстоятельств и меняющихся ситуаций, не отвлекаться от начатой работы, а доводить ее до конца, упорно и настойчиво осуществлять намеченные цели. Вот что по этому поводу говорил известный немецкий писатель Лессинг (1729-1781): "Самый медлительный человек, если он только не теряет из виду цели, идет быстрее, чем тот, кто блуждает бес-цельно".

Поэтому каждому из нас надо четко планировать свою работу на каждый день. Такое планирование следует оформить в виде режима дня и недельных расписаний - планов.

Думаю, что все знают, что такое режим дня. Это четкое перечисление всех основных видов деятельности в течение дня с указанием времени начала и конца каждого действия: в котором часу просыпаться, сколько времени отвести на физическую зарядку, на завтрак, в котором часу' начинаются и заканчиваются уроки в школе, когда надо приступить к выполнению домашних заданий и т. д.

Составить режим дня надо каждому самостоятельно, исходя из своих особенностей, учитывая домашние условия, свои интересы, привычки. Но, составив режим дня и убедившись в его разумности, его надо неукоснительно выполнять. Надо приучить себя к точному выполнению намеченного распорядка, как бы это ни было на первых порах трудно. Потом появится привычка к такому распорядку, и он уже не будет вызывать внутреннего сопротивления, желания его нарушать.

Однако режим дня лишь в общих чертах намечает характер работы в течение дня. Этого недостаточно для четкого планирования своего времени. Планирование содержания своей работы на каждый день можно оформить в виде недельных расписаний - планов.

Надо составлять два недельных расписания: одно постоянное на всю учебную четверть, в котором на каждый день недели указываются, какие уроки в этот день в школе, по каким учебным предметам в этот день выполняются домашние задания, в какие дни проводятся занятия в кружках, секциях, в какой день нужно выполнить значительные домашние дела и т. д.

Второе недельное расписание - план-еженедельник, составляется на каждую следующую неделю в конце текущей. В этом плане-еженедельнике указываем на каждый день недели выполнение каких-то новых возникших дел, общественных обязанностей, какую книгу собираемся прочитать, какой кинофильм и когда намечаем посмотреть. Туда же включаем те темы теле- и радиопередач, которые надо посмотреть и когда.

Конечно, этот еженедельник должен быть согласован с постоянным недельным расписанием и с режимом дня с тем, чтобы по возможности их не нарушать.

Имея режим дня, постоянное недельное расписание и еженедельник, мы четко знаем, что и когда нужно сделать, куда и зачем надо сходить. Конечно, жизнь может внести некоторые изменения в эти намеченные планы, могут возникнуть неожиданные ситуации, но, как правило, надо строго придерживаться намеченных планов и добиваться их безусловного выполнения.

Основное место и по времени и по значимости должна занимать у нас учебная работа, а она, как уже говорила Нина, есть умственный труд. Умственный же труд, как указывал великий русский педагог К. Д. Ушинский, "едва ли не самый тяжелый труд для человека. Мечтать легко и приятно, но думать трудно".

Поэтому необходимо рационализировать свой учебный труд, соблюдать правила гигиены умственного труда. Перечислим самые основные правила гигиены труда и рационализации своей работы.

1. Проверь, подходит ли тебе составленный режим дня, ведь у каждого свои условия, свои обстоятельства, свои особенности: у одних наибольшая работоспособность по утрам (жаворонки), а у других - вечером (совы). Кто ты - жаворонок или сова, понаблюдай за собой и в зависимости от этого построй свой режим дня. Посоветуйся с врачом, с родными, как лучше тебе организовать свой рабочий день. Но, уже составив свой режим дня, строго его выполняй!
2. Надо чередовать виды деятельности в течение дня: после умственных занятий работа по дому или занятия спортом будут отдыхом от напряженной умственной работы.
3. Утренняя физическая зарядка, обливание или обтирание холодной водой должны быть в режиме каждого дня.
4. Надо упорядочить прием пищи. Некоторые из нас утром ограничиваются стаканом чая, а потом на переменах жуют бутерброды. Это вредная привычка. Завтрак перед школой должен быть основательным, достаточно плотным. Полезно помнить восточную мудрость: завтрак съешь сам, обед раздели с другом, ужин отдай врагу. Во всяком случае, ужин не должен быть обильным и плотным и обязательно не менее чем за 3 ч до сна. На днях разговаривала на эту тему с одним учеником. Он сказал: "Я так привык. Понимаю, что это вредно, но ничего не могу сделать - привычка". Хочу ему и другим таким, как он, сказать, что это малодушие, что нет таких привычек, от которых нельзя избавиться, если они вредные. Герой гражданской войны, революционер М. В. Фрунзе (1885-1925) говорил: "Нужно совершенствоваться. Любой характер можно изменить. Терпение, способности, даже физическую силу - все можно выработать в себе, если по-настоящему захотеть, если не давать себе поблажки".
5. Надо приучить себя заранее готовиться к той или иной работе, заранее продумывать ее, планировать. Тогда легче и успешнее ее сделаешь. Это относится и к урокам математики. Зная тему предстоящего урока, полезно прочитать по учебнику дома перед уроками соответствующий параграф или пункт. Тогда будешь легче и основательней воспринимать объяснения учителя.
6. Очень важно организовать место для своей работы. В классе - разумно расположить на своем столе (парте) все нужные принадлежности, тетради. Дома - иметь постоянное, хорошо оборудованное место для работы: столик, полку для книг и учебников, для тетрадей, особое место для письменных и чертежных инструментов. Желательно иметь настольную лампу, а если ее нет, то так расположить свое рабочее место, чтобы свет падал с левой стороны.
7. Надо приучить себя правильно сидеть за рабочим столом: прямо, не изгибаясь в сторону, не подвертывая под себя ногу или еще как-то, чтобы не искривить позвоночник, ведь он у нас еще не окреп.
8. Во время длительной работы надо делать небольшие перерывы для отдыха, примерно через каждые 45 мин.
9. Работать надо равномерно, не спеша, но и не медля. При неудачах не горячиться, не нервничать, а спокойно и тщательно проверить проделанную работу, поискать причины неудачи. Если же ничего не найдешь, лучше отложить на время эту работу и взяться за нее вторично через некоторое время. Если и теперь неудача, не можешь, например, найти способ решения ка-кой-то задачи, можно, конечно, обратиться за консультацией к товарищам, к учителю. Но при этом постарайся понять, в чем твое упущение, почему ты сам не сумел найти правильное решение. Однако, если позволяет время, полезнее возвращаться к трудной, неподдающейся задаче не один или два раза, а многократно, чтобы в конце концов самому, без чужой помощи, подсказки, найти ее решение.
10. Вредно во время работы кушать. Если появилась жажда, можно выпить немного воды, а вот кушать погоди, пока не кончишь работу.
11. Не пытайся делать одновременно два дела: скажем, учить уроки и смотреть телевизор или слушать музыку. Это вредно для здоровья и для самой работы. Иные, выполняя домашние задания, включают на полную громкость магнитофон и под музыку джаза решают задачи. Толку от такой работы в музыкальном со-провождении мало. Если уж очень хочется музыки, то во время работы она должна быть тихой и спокойной. Но лучше приучить себя работать в полной тишине, работать сосредоточенно, отдаваясь целиком этой работе.
12. Полезно время от времени анализировать свою работу, ее организацию: все ли я делаю достаточно умело и рационально, что мне удается и что не удается, почему, нельзя ли что-то изменить в режиме дня, в способах работы или в ее организации, чтобы сделать ее более продуктивной.

Такой самоанализ поможет в лучшей организации самостоятельной работы, в повышении ее эффективности.

Полезно помнить советы Л. Н. Толстого (1828-1910) и следовать им: "Что назначено непременно исполнить, то исполняй, несмотря ни на что... Что исполняешь, исполняй хорошо... Никогда не справляйся в книге, ежели что-нибудь забыл, а старайся сам припомнить... Заставь постоянно ум твой действовать со всею ему возможною силою".

Занятие 2. Учитесь сравнивать

Должно быть, все вы не раз слышали крылатую фразу: "Все познается в сравнении". И действительно, оценить что-либо, установить, чем оно является, хорошо это или плохо, каков данный объект, можно, лишь сравнивая его с каким-либо другим. Я показываю вам карандаш и спрашиваю: большой он или маленький? Вы мне, очевидно, скажете:

- А по сравнению с чем? По сравнению с одним предметом он большой, а по сравнению с другим - он маленький.

Если я вам покажу несколько предметов и спрошу: какой из них самый большой, то вы вправе мне сказать, что вопрос поставлен неверно, он бессмысленный. Ведь не сказано, по какому свойству (признаку, параметру) надо установить наибольший предмет: по длине, по объему, по массе или еще по какому-либо параметру.

Вообще сравнивать предметы можно лишь по определенному общему свойству (признаку, параметру).

Если это свойство не указано, то вопрос о сравнении предметов не имеет смысла, сравнение невозможно.

Значит, для того чтобы сравнить предметы, объекты, надо сначала выявить их общие свойства, а лишь затем установить, по каким свойствам эти предметы сходны (одинаковы, равны), а по каким они различны (неодинаковы). Если же объекты таковы, что они вообще не имеют общих свойств, то их и сравнивать нельзя. Например, треугольник и многочлен не имеют, видимо, каких-либо общих свойств, а поэтому их и сравнивать нельзя. Треугольник можно сравнить с другим треугольником, с многоугольником, многочлен можно сравнить с другим многочленом, но между собой треугольник и многочлен сравнивать нет смысла.

А сравнивать математические объекты нужно, ибо только в сравнении мы познаем их наиболее важные свойства, изучаем их. Сравнивая треугольники между собой, мы устанавливаем, какие виды треугольников могут быть, сравнивая их с другими геометрическими фигурами, мы выявляем их особые свойства, например их жесткость: из трех отрезков можно образовать один и только один треугольник (если, конечно, эти отрезки удовлетворяют соотношению, что каждый из них меньше суммы двух других), а вот из четырех отрезков можно образовать не один четырехугольник, а много различных. Свойство жесткости треугольников очень важное, оно широко применяется в технике, в строительстве.

Поэтому вполне прав поэт Р. Сеф, который в шутливой форме писал:

Кто ничего,

Не замечает,

Тот ничего,

Не изучает.

Кто ничего

Не замечает,

Тот вечно хнычет

И скучает.

Сравним, например, медиану и биссектрису треугольника. Обе они являются отрезками, обе они соединяют вершину треугольника с какой-то точкой противоположной стороны, но медиана делит эту сторону пополам, а биссектриса делит угол при вершине пополам. Сравним теперь медиану и высоту треугольника. Они более резко различаются между собой, чем медиана и биссектриса. Это проявляется хотя бы в том, что медиана и биссектриса всегда находятся внутри треугольника, а высота может проходить и вне его.

Посмотрите на числа 4, 16, 38, 10. Сравните их, что в них общего? Пожалуй, лишь то, что все они натуральные числа и все четные. А вот числа 1, 4, 9, 16, 25, 36 имеют более существенное общее свойство: все они представляют собой квадраты последовательных натуральных чисел. Поэтому если нужно продолжить первую последовательность чисел, то после 10 можно поставить любое четное число, а вот во второй после 36 можно поставить лишь 49, затем 64, с тем чтобы сохранить замеченное общее свойство (закономерность) этих чисел.

Выявить общее свойство данных объектов не всегда легко. Например, по какому общему свойству (закономерности) написана следующая последовательность чисел: 16, 12, 15, 11, 14, 10?

Сравнивая эти числа попарно, замечаем: 16-4=12, 12+3=15, 15-4=11, 11+3=14, 14-4=10.

Значит, числа этой последовательности составлены так, что последующее число получается из предыдущего попеременно то вычитанием 4, то прибавлением 3. Поэтому если надо приписать к ней еще два числа, то можно написать такие числа: 10+3=13 и 13-4=9.

Но можно заметить и такое общее свойство чисел этой последовательности: она составлена из двух очень простых последовательностей: 16, 15, 14 и 12, 11, 10, причем члены второй последовательности расставлены между членами первой. Значит, чтобы приписать еще два числа к этой последовательности, продолжаем каждую из составляющих: 16, 15, 14, 13 и 12, 11, 10,9 - и затем члены второй последовательности расставляем между членами первой: 16, 12, 15, 11, 14, 10, 13, 9.

Для нахождения общего свойства членов последовательности нам пришлось сравнивать между собой числа. Как известно, для сравнения чисел существуют два основных способа: разностное и кратное сравнение. При разностном сравнении мы находим разность этих чисел и по ней судим, какие из данных чисел больше, а какие меньше и на сколько. При кратном сравнении положительных чисел мы находим их частное и по нему в зависимости от того, больше оно или меньше 1, судим, какое из данных чисел больше, а какое меньше и во сколько раз.

Так, сравнивая разностным способом числа 4 и 12, находим, что 12-4 = 8, Это значит, что 12 больше 4 на 8 или 4 меньше 12 на 8. Сравнивая эти же числа кратным способом, находим, что 4:12=1/3 или 12:4=3. Это значит, что 4 меньше 12 в 3 раза или составляет 1/3 от 12, а 12 больше 4 в 3 раза.

Вы хорошо знаете способ сравнения отрезков путем непосредственного наложения их друг на друга. Точно так же путем наложения можно сравнивать углы. В результате такого непосредственного сравнения числа, отрезки, углы можно расположить по порядку возрастания или убывания. Точно так же можно сравнивать между собой квадраты, круги. А вот уже прямоугольники так сравнивать нельзя. Для их сравнения, так же как и для сравнения других фигур, в математике разработан метод опосредственного сравнения с помощью измерения.

Для этого сравниваемые объекты измеряют с помощью одной и той же единицы измерения, а затем сравнивают полученные числа. Так, для сравнения двух прямоугольников по площади их измеряют с помощью единицы измерения - квадрата - со стороной, равной единице длины, после чего остается сравнить полученные числа.

Эти два способа сравнения однородных объектов можно наглядно увидеть при нахождении массы тела. Когда мы сравниваем два предмета с помощью чашечных весов без гирь, то это способ непосредственного сравнения; когда же для сравнения этих же предметов их взвешивают на весах с помощью гирь,т. е. находят численную величину их массы, а затем сравнивают полученные числа, то это уже способ опосредственного сравнения.

Заметим, что два объекта можно сравнивать не по одному какому-то свойству (признаку), а, как правило, по разным и многим признакам (основаниям сравнения). Например, треугольники можно сравнивать по площади, по периметру, по виду углов (сравниваемые треугольники могут быть оба остроугольными или один из них остроугольный, а другой тупоугольный и т. д.), по соотношению сторон (например, один из них равнобедренный и т. д.) и еще по другим основаниям.

Сложнее сравнивать алгебраические объекты: многочлены, уравнения, тождества, функции и т. д. Так, сравнивая между собой многочлены, можно лишь установить, различаются ли они по числу переменных или по наивысшей степени переменных. Можно, конечно, их сравнить и по тому, какие буквы входят в эти многочлены: одни и те же или разные. Но это различие не-существенное, ибо, например, многочлены х²+ху+у²и а²+ab+b² существенно не различаются: по сути дела это один и тот же многочлен.

Как видим, сравнение лежит в основе классификации объектов, а измерение есть способ сравнения, и в то же время само измерение производится с помощью сравнения измеряемого объекта с единицей измерения.

В основе решения большинства задач также лежит сравнение. А многие задачи прямо связаны со сравнением.

Занятие 3. Развивайте внимание и волю

Для того чтобы видеть любой математический объект во всем многообразии его свойств, чтобы сравнивать объекты, видеть их сходства и различия, надо обладать хорошо развитым вниманием.

На человека постоянно воздействуют много самых различных объектов. Но он не может охватывать с достаточной ясностью все эти объекты: одни он видит, слышит, осязает отчетливо, ясно, другие же смутно, нечетко либо вовсе не видит, не осязает. Из всей массы объектов, так или иначе воздействующих на человека в данный момент, он выделяет лишь один или несколько, которые для него интересны, важны, соответствуют его потребностям, его целям. Без такого сосредоточенного выделения отдельных объектов, на которые направляются наши органы чувств (зрение, слух, обоняние и т. д.), и отвлечения от всех других объектов, находящихся также в поле нашего восприятия, невозможна была бы никакая сознательная, целенаправленная деятельность.

Вот эта направленность и сосредоточенность нашего восприятия на определенных объектах или определенной деятельности при отвлечении от всего остального и называется вниманием.

Образно внимание определяют как дверь, через которую проходит в наше сознание все из внешнего мира.

Для того чтобы хорошо учиться, плодотворно работать, надо уметь открывать эту дверь, управлять ею, чтобы в наше сознание вошло значимое, ценное, а не какие-либо пустяки, которые только засоряют наш ум.

Различают непроизвольное (непреднамеренное) и произвольное (преднамеренное) внимание. Непроизвольное внимание - это внимание, возникающее без всякого намерения человека. Это такое внимание, когда дверь в наше сознание открывается сама по себе, не управляемо. Такое внимание характерно для маленьких детей, они еще не умеют управлять своим вниманием.

Вы же должны уметь управлять своим вниманием, уметь открывать дверь в свое сознание, лишь имея определенную цель. Это и значит, что вы должны обладать достаточно развитым произвольным вниманием. Вы должны уметь управлять вниманием и направлять его на нужный объект, на значимую для вас деятельность.

Есть много разных способов проверки уровня развития произвольного внимания. Вот один из них.

Сделайте из плотной бумаги или картона 6 карточек со следующими таблицами:

В каждой таблице написаны числа от 1 до 25 в беспорядке. Вам же необходимо внимательно рассмотреть таблицу и отыскать все числа по порядку от 1 до 25. Время, затраченное на поиск, нужно фиксировать по секундомеру (или по обычным часам с секундной стрелкой). Если вы затрачиваете на каждую таблицу не более 30-35 с, то у вас развито внимание, если же больше, то слабо. Проследите также, как меняется затрачиваемое вами время от таблицы к таблице. Если оно резко меняется, то у вас неустойчивое внимание.

С помощью этих таблиц можно тренировать свое внимание. Для этого надо через некоторые промежутки времени, не менее часа, повторять работу с этими таблицами. Если постепенно по мере тренировки затрачиваемое время сокращается и при переходе от таблицы к таблице не меняется существенно, значит, внимание ваше развивается. Когда вы добьетесь, что на каждую таблицу вы будете затрачивать не более 15 с, то можете считать, что развили свое внимание вполне достаточно.

Вот другой способ проверки внимания. Разбейтесь на пары. Один из пары задает другому какое-либо двузначное число, например 43. Второй должен в течение 5 мин в хорошем темпе, не останавливаясь, прибавить к этому числу первую цифру 4, назвать сумму 47 и снова прибавить к этой сумме первую цифру назвать сумму 51, прибавить первую цифру 5, назвать сумму 56 и т. д. Первый должен следить за правильностью второго и незаметно фиксировать ошибки. Если за 5 мин вы сделаете лишь 3 ошибки, то ваше внимание хорошо развито; если же число ошибок больше или вы в процессе работы останавливались, то вам следует тренировать свое внимание.

Это испытание внимания можно усложнить, а именно надо к заданному числу прибавлять попеременно то первую, то вторую цифру или попеременно прибавлять и отнимать первую и вторую цифры.

Еще один простой способ проверки и тренировки внимания. Составьте таблицу из 20 двадцатизначных чисел, например таких:

По команде товарища, который проверяет ваше внимание, нужно вычеркнуть все какие-либо три цифры, которые вам назовет товарищ, например 0, 1 и 3. Эту работу следует проделать не более чем за 5 мин. После этого необходимо подсчитать число правильно зачеркнутых цифр, из него вычесть число допущенных пропусков и ошибочно зачеркнутых цифр. Затем найти процентное отношение полученного числа к общему числу цифр 0, 1, 3 в данной таблице, т. е. к числу 149. Если это отношение не менее 80%, то это неплохо, если же оно менее 80%, то вам надо тренировать свое внимание.

Упражнения с этой таблицей можно начать с вычеркивания одной какой-то цифры, затем двух цифр и лишь после того, как вы справитесь с этими заданиями, перейти к вычеркиванию трех цифр.

Развитие произвольного внимания, так же как и многих других качеств человека, связано с укреплением воли. Воля человека позволяет ему управлять и регулировать свою деятельность, управлять своими поступками. Когда вы умеете четко выполнять режим дня, умеете заставлять себя предельно внимательно слушать урок, доклад, выполнять аккуратно все домашние задания, то тем самым вы проявляете свою волю. Очень важно укреплять свои волевые качества, тренировать себя для развития этих качеств. Ведь настоящий человек - это человек с сильной волей!

Когда вы ставите перед собой задачу внимательно выполнить те или иные задания на проверку внимания, а затем добиваетесь путем тренировки достижения нужного развития произвольного внимания, то этим самым вы не только развиваете свое внимание, но и укрепляете свою волю. То же самое происходит при выполнении вами всех других заданий.

Имеются и особые методы по укреплению своей воли, своих волевых качеств. Вот один из простейших.

Прикрепите к стене лист белой бумаги с нанесенной на нем хорошо видимой точкой. Сядьте на некотором расстоянии перед этим листом в удобной позе и попытайтесь сосредоточить все свое внимание на этой точке. Причем точка должна быть все время в центре вашего внимания: кроме точки, вы ничего не должны видеть и ни о чем другом не думать.

На первых порах, должно быть, вы сумеете сосредоточить свое внимание на рассматриваемой точке не более 15-20 с. Затем точка начнет расплываться, как бы уходить из поля зрения. В голову начнут лезть совершенно посторонние мысли, которые и уводят ваше внимание от рассматриваемой точки.

Но если вы будете часто тренироваться, скажем раз в день или через день, в удержании своего внимания на этой точке, то постепенно достигнете хороших результатов и тем самым разовьете свою волю. Однако это развитие воли надо укреплять и в повседневной своей работе, в своем поведении.

Задание 11

11.1. Найдите в приведенных примерах все 12 допущенных ошибок. На эту работу вы должны затратить не более 3-4 мин. После этого еще раз себя проверьте, не пропустили ли вы ошибки или подчеркнули там, где нет ошибки.

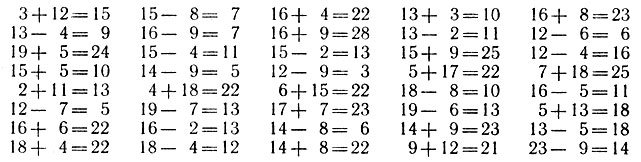
11.2. Решите быстро следующие задачи:

а) На лесопильном заводе машина за 1 мин отпиливает от бревна кусок длиной 2 м. За сколько минут будет распилено на такие куски бревно длиной 10 м?

б) Какова длина бревна, на распиловку которого на такие куски машина затратила 6 минут?

в) За сколько времени будет распилено таким образом бревно в 16 м?

г) Сколько распилов надо сделать, чтобы распилить на такие куски бревно в 12 м?

Занятие 4. Укрепляйте свою память

За годы обучения математике вы получите огромное число самых различных знаний, и их надо помнить. Если вы что-то важное забудете, то не сумеете решить задачу, доказать новую теорему. Значит, для изучения математики нужно иметь хорошую память. Хорошую память надо иметь и для будущей работы, для повседневной жизни. Если вы что-то делаете хорошо, быстро и легко, этому способствует хорошая память. А представьте себе, во что превратилась бы наша жизнь, если бы мы вдруг потеряли память? Мы бы не знали, что и как делать, и всякий раз вынуждены были заново изучать и осваивать любое самое простейшее действие, а после этого снова забывали бы его. Нормальная жизнь была бы невозможна.

Память надо развивать и укреплять. И при этом очень важно учесть следующее обстоятельство: для изучения математики надо иметь хорошую память, и в то же время в процессе рационального и разумного изучения математики ваша память совершенствуется и укрепляется. Если же учение вами организовано неразумно, нерационально, то тем самым можно не только не укрепить свою память, а ее разрушить, искалечить. Это относится, конечно, Fie только к памяти, но и ко всем другим качествам, особенно к мышлению.

Память - это запоминание, сохранение и воспроизведение всего того, что было в нашем опыте, в восприятии и действии.

Существуют разные виды памяти: двигательная (запоминание, сохранение и воспроизведение различных движений, например ходьбы, письма и т. д.), эмоциональная (память на чувства, переживания), образная (память на представление, она бывает зрительной, слуховой, осязательной, обонятельной, вкусовой; наибольшее значение для изучения математики имеет, конечно, зрительная и слуховая память) исловесно-логическая (память на мысли, понятия, знания - это наиболее важный вид памяти для изучения математики, именно с ее помощью вы и овладеваете всеми премудростями математики).

Память делят также на (непреднамеренную) и произвольную (преднамеренную). Когда мы что-то запоминаем, сохраняем и можем воспроизвести, не ставя перед собой цель запомнить, а запоминаем попутно в процессе деятельности, то это и есть непроизвольная память. Когда же мы ставим такую цель, то говорят о произвольной памяти. В процессе учения имеют значения оба вида памяти. Конечно, было бы хорошо все запомнить как бы попутно, в процессе вычислений, доказательств, выводов, без специальных усилий на запоминание. Но это не всегда возможно, и вы должны научиться управлять своей памятью, руководить ею и ставить перед собой в нужных случаях цель прочно и надолго запомнить изученное.

Непроизвольное запоминание, как уже было сказано, происходит главным образом в деятельности, в действиях с математическими объектами. Когда вы решаете задачи, выводите формулы, доказываете теоремы и при этом активно используете те или иные знания, правила и законы, то тем самым вы непроизвольно эти знания, правила и законы запоминаете.

Поэтому лучший и наиболее рациональный способ запоминания знаний - это их активное и многократное использование. Решаете задачи, доказываете теоремы и при этом припоминайте и формулируйте все те знания, на основе которых решаются задачи и доказываются теоремы, и вы тем самым без всяких на то специальных усилий хорошо и прочно запомните все эти знания. Но для этого надо обязательно, во-первых, ставить цель понять и освоить все эти знания, а во-вторых, припомнить и полно формулировать используемые знания.

Однако в ряде случаев приходится и специально ставить цель что-то запомнить, заучить. Для этого используются разные способы рационального запоминания. Самый нерациональный, неразумный, даже вредный способ - это зубрежка, механическое и многократное повторение одного и того же учебного материала. Ни в коем случае не занимайтесь зубрежкой, ибо вы можете тем самым искалечить свой ум, свою память.

Рациональные способы произвольного запоминания - это такие, которые основаны на понимании, на логическом осмыслении запоминаемого. Значит, чтобы что-то заучить, надо захотеть запомнить, затем понять и осмыслить материал, который вы заучиваете, для чего разбить его на составные (смысловые) части, продумать каждую часть, выделить в ней главное содержание, основную идею, дать каждой части свое название (тем самым составить план заучиваемого материала), сравнить с другими, ранее изученными знаниями и тем самым ввести заучиваемое в систему ваших знаний.

Иногда можно использовать и особые приемы для запоминания. Все такие приемы называются мнемоническими, от имени древнегреческой богини памяти Мнемозины. Например, чтобы запомнить первые цифры числа π, придуманы разные фразы, число букв, в каждом слове которых есть цифра числа я. Вот одна из таких удачных фраз:

"Это я знаю и помню прекрасно".

3 1 4 1 5 9… , которая дает вполне достаточное по точности значение числа π=3,14159... .

В процессе изучения математики используются два типа памяти: кратковременная и долговременная.

Когда мы что-то вычисляем, преобразуем, то все промежуточные результаты и сами условия мы помним лишь до завершения работы, а затем забываем. Это хорошо и разумно, ибо для чего засорять свою память ненужными данными, ведь они нам нужны лишь для решения данной задачи, а для последующей работы они вовсе не нужны. В этом случае действовала лишь одна кратковременная память.

Долговременная память возникает тогда, когда некоторые из внешних воздействий (знаний, фактов, понятий и т. д.), имеющих особое для нас значение, перерабатываются в нашем уме, осмысливаются, и тогда они переходят в долговременную память и запоминаются надолго. Таким образом, при восприятии и деятельности все воспринимаемое как бы сортируется: одни из этих восприятий отправляются в кратковременную память и затем выбрасываются, забываются; другие же осмысливаются, перерабатываются и отправляются в долговременную память, где сохраняются достаточно долго. Процесс перехода воспринимаемого материала в долговременную память требует известного времени (от получаса до часа), в то время как процесс кратко-временного запоминания происходит мгновенно.

Проверить свою кратковременную память можно, например, таким образом. Приготовьте на листе бумаги следующую таблицу:

С помощью этой таблицы можно производить проверку как зрительной, так и Слуховой кратковременной памяти. Способ проверки слуховой памяти: попросите кого-либо называть вам сначала числа первой строки, после чего вы их записываете, затем называть числа второй строки, после этого вы записываете эти числа и т. д. Если вы сумеете записать по памяти все числа не выше 3-4-й строки без ошибок, то у вас вполне нормальная слуховая кратковременная память.

Для проверки зрительной памяти надо открывать по порядку каждую строчку таблицы, рассматривать ее в течение примерно полминуты, затем, закрыв таблицу, воспроизвести по памяти числа данной строчки. Если вы сумеете безошибочно воспроизвести все числа не выше 3-4-й строчки, то у вас нормальная память.

Вот другой способ. Попросите кого-либо, чтобы он нарисовал на листе бумаги 12 геометрических фигур, например: правильный треугольник, окружность, квадрат, окружность со вписанным треугольником, окружность с описанным квадратом, параллелограмм, прямоугольник, трапецию, ромб, пару вертикальных углов, треугольник с вписанным квадратом, ромб с вписанной окружностью. И все эти фигуры пусть он раскрасит двумя цветами, притом сложную фигуру, состоящую из двух, надо раскрасить двумя цветами; получится, например, красный круг с синим треугольником или синий квадрат с красным кругом и т. д.

Вам показывают этот рисунок, и вы его должны внимательно рассматривать в течение одной минуты. Затем, закрыв рисунок, вы по памяти должны назвать все нарисованные фигуры. Если вы правильно вспомните не менее 8 фигур, то у вас вполне нормальная память.

Если ваша память (слуховая, зрительная или образная) оказалась несколько ниже нормы, то с помощью указанных способов можно тренировать свою память, для чего нужно соответствующую проверку повторить до тех пор, пока вы не достигнете нормы, при этом промежуток между повторными проверками должен быть не менее часа, а лучше сутки.

Одно из свойств памяти, которое следует особо учитывать,- это забывание. Проделайте такой опыт. Пусть ваш товарищ назовет вам 8 цифр в случайном порядке. Вы должны тут же их повторить. Если вам удастся повторить не менее 6 цифр, то это вполне нормально. Затем проверьте, сколько из этих цифр вы сумеете повторить через 1 мин, затем через 2 мин, через 5 мин. Вы убедитесь, что сумеете повторить уже не все цифры, которые вы повторили первоначально, а значительно меньше. Это и есть забывание.

Забывание происходит как того, что запомнилось кратковременной памятью, так и того, что взошло в долговременную память. Поэтому, для того чтобы что-то запомнить прочнее и надолго, надо это (знание) неоднократно использовать и повторять. При этом лучший способ - это многократное использование с активным воспроизведением этого знания в процессе использования.

Согласно исследованиям забывание происходит наиболее бурно в первые дни после запоминания. Вот почему важно повторить изученное на уроке в тот же день или в крайнем случае через день с тем, чтобы приостановить процесс забывания.

В заключение приведем некоторые правила заучивания учебного материала.

1. Заучивай лишь то, что понимаешь. Надо сначала понять, а уже потом ставить цель заучить, запомнить.
2. Заучивая, ставь цель запомнить надолго.
3. Пользуйся при заучивании смысловыми опорами. Для этого разбивай заучиваемый материал на логические части, обозначай каждую часть своим названием, передающим смысл этой части. Эти названия и будут служить смысловыми опорами.
4. Заучивай и повторяй небольшими дозами.
5. Лучше учить частями несколько дней, чем все в один день.
6. Нельзя заучивать учебный материал по математике, лишь читая его по учебнику или тетради (вслух или про себя). Надо обязательно этот материал воспроизводить на бумаге: нарисовать чертеж, написать схему теоремы и ее доказательства и т. д., т. е. заучивать надо в действии.
7. Старайся воспроизвести заучиваемый материал по памяти, а не глядя в книгу.

Занятие 5. Развивайте свое воображение и мышление

Вся математика есть результат деятельности воображения и мышления человека. Ведь математические объекты реально не существуют, их нет в природе, вокруг нас, они - плод воображения и мышления, но отражающие предельно точно этот окружающий нас мир.

В окружающем нас мире нет геометрических фигур, нет чисел и функций, нет многочленов и уравнений. Но в этом мире есть предметы, имеющие форму, есть совокупности предметов, имеющие величину и количество, происходят явления и процессы, в которых предметы находятся в каких-то меняющихся отношениях. Однако, для того чтобы отделить форму от предметов, величину и количество от их совокупности, отношения от явления и процессов и сделать эти формы, величины, количества и отношения самостоятельными объектами, нужна была огромная работа в течение тысяч лет человеческого воображения и мышления.

Поэтому и изучение математики, овладение ею требует развитого воображения и мышления. Нужно упорно учиться видеть и действовать в уме. Учитель говорит: "Если повернуть параллелограмм вокруг точки пересечения диагоналей на 180°, то, как вы думаете, совпадает ли он со своим первоначальным положением?". Чтобы правильно ответить на этот вопрос, мы должны мысленно представить себе то, о чем говорил учитель: увидеть параллелограмм с диагоналями, увидеть процесс его поворота вокруг точки пересечения диагоналей, и тогда вы сможете точно, а не наугад ответить на заданный вопрос. Вы читаете в учебнике: "В ΔABC проведены из вершины С высота, биссектриса и медиана". И вы должны вообразить этот треугольник AВС, увидеть, что его стороны АС и СВ не равны, ибо в противном случае высота, биссектриса и медиана просто слились бы, увидеть, что высота проходит ближе к меньшей стороне, а биссектриса и медиана - ближе к большей стороне, но вот неясно, проходит ли биссектриса между высотой и медианой или же медиана между высотой и биссектрисой. Это уже требует особого исследования.

Однако надо не только видеть в уме услышанное или прочитанное, но надо уметь и действовать в уме. Вам надо разделить 235 698 на 2. Неужели вы будете это делать углом? Нет, вы должны сразу писать ответ, выполняя все промежуточные действия в уме. Или вам надо преобразовать алгебраическое выражение, уравнение, неравенство. И опять-таки многие промежуточные преобразования надо выполнять в уме, устно.

Умение видеть и действовать в уме особенно вам понадобится, когда вы начнете изучать стереометрию - геометрию в пространстве. Ведь бумага, на которой вы можете чертить, изображать изучаемые в стереометрии пространственные фигуры, плоская. Поэтому без воображения, без умения видеть и действовать в уме вы не сможете понять никакой чертеж, никакое изображение пространственных фигур. С необходимостью видеть и действовать в уме вы встретитесь и на любой работе. Токарь, слесарь, конструктор, технолог, архитектор, строитель должны уметь по плоскому чертежу увидеть сложную пространственную деталь, сооружение или машину. Геолог, географ, военный, агроном должны уметь по карте или плану увидеть все особенности местности, сориентироваться на ней. Для того чтобы разумно выполнить некоторую работу, надо предварительно ее спланировать, "проиграть" в уме, а уже затем начать действовать.

Математика изучает общие свойства бесконечных совокупностей математических объектов. Когда вы доказали, что сумма углов треугольника равна 180°, то тем самым вы установили, что этим свойством обладает любой треугольник, а их бесконечное множество. Но чтобы это свойство установить, надо было сначала его заметить, сформулировать и уже потом доказать. Человечество приходило к математическим истинам не сразу, а постепенно, замечая свойства отдельных объектов, а затем обобщая их. Еще древние египтяне знали, что треугольник со сторонами 3, 4 и 5 прямоугольный, и пользовались этим для построения прямого угла на местности. Но прошло много сотен лет, пока это частное свойство одного треугольника было обобщено для любых прямоугольных треугольников и была доказана теорема, обратная теореме Пифагора.

Значит, важно учиться обобщать единичные факты, наблюдения. Вот вы наблюдаете такие факты: ;

И из этих наблюдений вы должны суметь сделать такое обобщение:

Конечно, это обобщение затем надо будет доказать.

Здесь проявляется ваша сообразительность, умение делать догадки. А ведь сообразительность и основана на умении видеть общее в частном, видеть сходство в различном.