Лабораторна робота з теми «Властивості тригонометричних функцій. Побудова графіків тригонометричних функцій»

Лабораторна робота з теми

«Властивості тригонометричних функцій. Побудова тригонометричних функцій»

Мета: навчитися будувати графіки тригонометричних функцій методом геометричних перетворень.

Прилади: олівець, лінійка, картки підказки, таблиця даних тригонометричних функцій числового аргументу

Теоретичні відомості

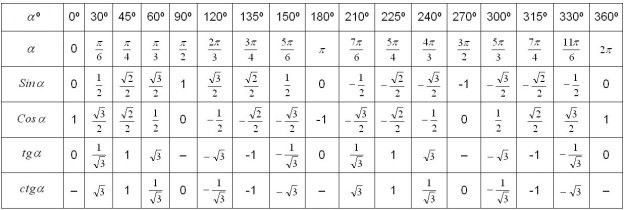
Графік кожної з тригонометричних функцій досить побудувати на проміжку, що дорівнює найменшому додатному періоду, а потім його можна продовжити на всю область визначення. При побудові графіків за точками скористаємось таблицею значень тригонометричних функцій числового аргументу (табл. 1).

Табл. 1

 

Завдання 1

На одній координатній площині побудувати графіки функцій ; ;

1. Заповнити таблицю значень

	0				π				2π	3π	4π

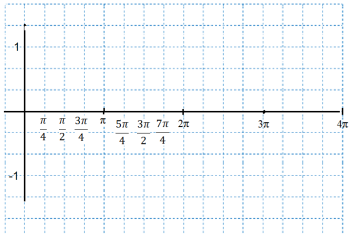2. Побудувати графіки функцій (синусоїди):

Оскільки функція  періодична з періодом 2πk, де , тобто , то для продовження графіка за межі відрізка [0;2π] досить виконати побудову графіків виду ; ;

; ; ., паралельно переносячи графік функції вліво і вправо.

3. Висновок: для графіків тригонометричних функцій виду

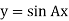
 І      Якщо А>1, графік функції стиснюють у А рази до осі ОУ

ІІ       Якщо 0<А<1, графік функції розтягуючи у А раз від осі ОУ.

 

Завдання 2

На одній координатній площині побудувати графіки функцій ; ;

1. Заповнити таблицю значень

	0		π		2π

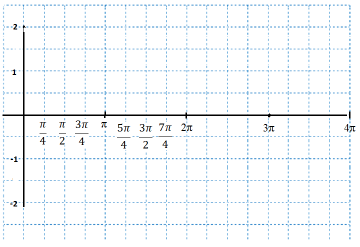
2. Побудувати графіки функцій (косинусоїди):

 

3. Висновок: для графіків тригонометричних функцій виду

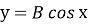
 І        Якщо B>1, графік функції розтягуючи у А рази від осі ОХ

ІІ       Якщо 0<B<1, графік функції стискають у А раз до осі ОХ.

 

Завдання 3

На одній координатній площині побудувати графіки функцій ; ;

Заповнити таблицю значень

					0				π

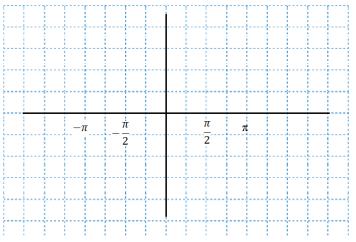
Побудувати графіки функцій (тангенсоїди):

Висновок:

 

 

 

 

 

 

 

 

 

Завдання 4

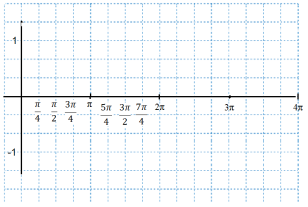Побудувати графіки функцій:

А) ; 

Заповнити таблицю значень

 

	0		π		2π

Побудувати графіки функцій (синусоїди):

Висновок:

 

 

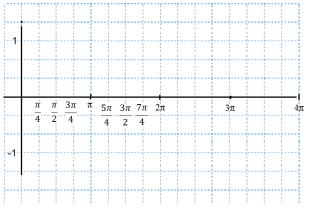
Б) ; 

Аналіз: оскільки функція   непарна і  , тому графік функції ;

  співпадає з графіком функції

 

Висновок:

 

 

 

В)   і 

Аналіз: функція парна от же

  , тому графік функції

  співпадає з графіком функції

 

Висновок:

 

 

 

Завдання 5

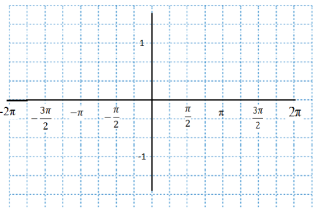
А) побудувати графік функції    і

 

 

1. Побудувати графіки функцій (синусоїди):

Оскільки функція парна, тому достатньо побудувати графік функції для і симетрично відобразити його відносно осі ординат

Висновок:

 

 

 

 

 

 

 

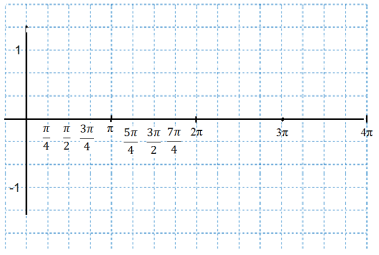
Б)   і 

Заповнити таблицю значень

	0		π		2π

 

 

 

 

 

 

 

 

 

 

 

 

 

Висновок лабораторної роботи:

Побудова графіків тригонометричних функцій методом геометричних перетворень виконується за певними законами:

1. Графік функції y=f(x) 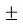a, де a>0 можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі ОУ на а одиниць угору, якщо а>0, і на а одиниць униз, якщо а<0.
2. Графік функції y=f(x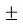b), де b>0 можна одержати із графіка функції y=f(x) за допомогою паралельного перенесення вздовж осі ОX на b одиниць ліворуч, якщо b>0, і на b одиниць праворуч, якщо b<0.
3. Графік функції y=-f(x) можна одержати із графіка функції y=f(x) за допомогою симетричного відображення останнього відносно осі абсцис (ОХ).
4. Графік функції y=f(-x) можна одержати із графіка функції y=f(x) за допомогою симетричного відображення останнього відносно осі ординат (ОУ)
5. Графік функції y=сf(x) можна одержати із графіка функції y=f(x) за допомогою розтягу графіка функції y=f(x) від осі абсцис у с  разів, якщо с>1,  або стиску до осі абсцис у разів , якщо 0<с<1.
6. Оскільки функція 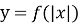парна, тому достатньо побудувати графік функції 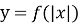для 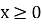і симетрично відобразити його відносно осі ординат