Тема:  Найбільше та найменша значення функції.

Мета заняття :

              сформувати в учнів уявлення про найбільше і найменше значення функції; вивести алгоритм знаходження їх на даному проміжку. Формувати вміння застосовувати виведений алгоритм до знаходження максимального та мінімального значення функції на проміжку. Розвивати комунікативні здібності, увагу, уміння лаконічно й математично грамотно висловлювати свою думку. Виховувати працелюбність, інтерес до предмету.

Методи: репродуктивні, пояснювально – ілюстративні, практичне виконання вправ, бесіда

Матеріально-технічне забезпечення та дидактичні засоби: таблиця, дидактичні матеріали

Література:

1) Алгебра і початки аналізу: підручник для 10 кл. загальноосвіт. навч. закладів/   М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук;.  – К.: Зодіак – ЕКО, 2003. -  272 с.

2) О.С.Істер«Збірник задач і завдань для тематичного оцінювання з алгебри і початків аналізу для 11 класу». –Харків, Гімназія», 2001

           Структура заняття                                                                Відведений час

1. Організаційна частина: контроль відвідування                                              3 хв

2.Повідомлення теми, формування мети та                                                   2 хв

основних завдань

3. Актуалізація питань  (питання контролю):                                              10 хв 

• Опитування теоретичного блоку з використанням технології «Незакінчене речення».
  1. Похідною функції в точці називають…
  2. Геометричний зміст похідної полягає в тому, що…
  3. Механічний зміст похідної полягає в тому, що…
  4. Рівняння дотичної до графіка функції має вигляд…
  5. Щоб знайти похідну складеної функції потрібно похідну…
  6. Критичні точки – це точки у яких…
  7. Точки екстремуму – це точки…
  8. Точка максимуму – це точка у якій похідна…
  9. Точка мінімуму – це точка, у якій похідна…
  10. Похідну добутку шукають за формулою…
  11. Похідну частки шукають за формулою…
• Усне знаходження похідних деяких простих функцій:

4.Контроль вихідного рівня знань студентів:                                            10 хв

Повторення основних схем дослідження:

• На монотонність;
• На точки екстремуму;
• На екстремум;
• На найбільше та найменше значення функції.

5. Інструктаж вступний .

6.Формування умінь і навичок. Перелік практичних                               50 хв

 завдань.   

• Знайти найбільше та найменше значення функції на відрізку:

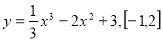
        Знайдіть найбільше і найменше значення функції f(x) = x + e^-x на відрізку [-1; 2].

Розв'язання

Знайдемо значення функції в точках x = -1 та x = 2:

f(-1) = -1 + e^l  = e – l,  f(2) = 2 – е ^-2 = 2 –   .

Знайдемо f’(x): f'(x) = (x + е^-x)¹ = 1 - е^-x. Знайдемо стаціонарні точки:

f'(x) = 0;  1 - е^-x = 0; 1 - = 0; е^x = 1; x = 0.

Знайдемо значення функції в точці x = 0: f(0) = 0 +е°= 1.

Із чисел е - 1 1,72, 2 - 1,86 та 1 найбільшим є 2 - , а   найменшим -1.

Відповідь: f_найб. = f(2) =2 - ; f_найм. = f(0) = 1

• При розв'язуванні деяких задач потрібно знаходити найбіль­ше або найменше значення функції не на відрізку, а на інтервалі.

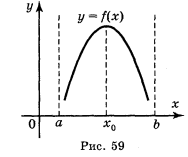
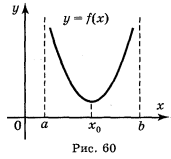
В практичних задачах функція f(x) має на заданому інтервалі тільки одну стаціонарну точку: або точку максимуму, або точку мінімуму. У цих випадках у точці максимуму функція f(x) при­ймає найбільше значення (рис. 59), а в точці мінімуму — най­менше значення на даному інтервалі (рис. 60).

• Знайдіть найменше значення функції у = х+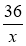, де х є (0; 10).

Розв'язання

Знайдемо похідну у’ =1 – = 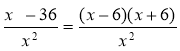. Стаціонарні точки x₁= 6, х₂ = -6. На інтервалі (0; 10) є тільки одна стаціонарна точка x = 6. При переході через цю точку похідна змінює знак з «–» на «+» , і тому x = 6 — точка мінімуму. Отже, f _найм. = f(6) =12.

Відповідь: f _найм. = f(6) =12.

• Правила знаходження найбільшого і найменшого значення функції часто використовують при розв'язуванні прикладних задач. При цьому керуються такою схемою:

1) задачу «переводять» на мову функцій. Для цього вибирають зручний параметр х, через який виражають як функцію у = f(x) величину, яка нас цікавить;

2) засобами аналізу знаходять найбільше чи найменше значен­ня цієї функції на деякому проміжку;

3) з'ясовують, який практичний зміст (у межах даної задачі) має отриманий (на мові функцій) результат.

Задача 1. Число 20 запишіть у вигляді суми двох невід'ємних доданків так, щоб добуток їхніх квадратів був найбільшим.

Розв'язання

Нехай перший доданок дорівнює х, тоді другий доданок дорівнює 20 – х, причому х є [0; 20].

Добуток квадратів цих доданків дорівнює (20 – х)² · х². Отже, задача зводиться до знаходження такого х, при якому функція f(x) = (20 - х)² · х² набуває найбільшого значення на відрізку [0; 20].

Знайдемо похідну f'(x) = 2(20 - х) · (20 - х)' х² + (20 - х)² · 2х = -2x²(20 - х) +   + (20 - х)² · 2х = 2х(20 - х)(20 – 2х).

Стаціонарними точками функції є точки 0; 20; 10. Тоді

f(0) = (20 – 0)² · 0² = 0;     f(l0) = (20 - 10)² · 10² == 10 000; 

f(20) = (20 - 20)² · 20² = 0.

Отже, f_найб. = f(10) = 10 000. Таким чином, число 20 слід подати у вигляді  20 = 10 + 10.

Відповідь: 20 = 10 + 10.

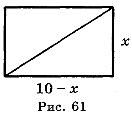Задача 2. Серед прямокутників, що мають периметр 20 см, знайти той, діагональ якого найменша.

Розв'язання

Нехай довжина однієї із сторін шуканого прямокутника х см, тоді друга сторона дорівнює (10 - х) см, де 0 < х < 10. Тоді (рис. 61) діагональ у прямокутника виражаєть­ся формулою у ==. Знайдемо стаціонарні точки:

у' = 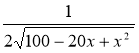  · (100 - 20х + 2х²)' = 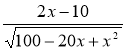; y’ = 0; 2x – 10 = 0;

 х= 5.

Якщо 0 < х < 5, то y' < 0, тобто функція спадає, якщо 5 < х < 10, то у' > 0, і функція зростає. Отже, найменше значення функції у = на інтервалі (0; 10) дорівнює y_найм = y(5) = = 5.

Таким чином, найменшу діагональ 5см матиме квадрат зі стороною 5 см. Відповідь: квадрат зі стороною 5 см.

Розв'язування вправ

1. Число 36 записати у вигляді добутку двох додатних чисел, сума яких найменша.

Відповідь: 36 = 6 · 6.

2. Парканом довжиною 80 м треба огородити прямокутну ділян­ку найбільшої площі. Знайдіть розміри ділянки.

Відповідь: 20 х 20 м.

3. Із усіх прямокутників, площа яких дорівнює 9 см², знайдіть прямокутник з найменшим периметром.

Відповідь: квадрат зі стороною 3 см.

7. Поточний контроль виконання роботи                                                       2 хв

Виставлення оцінок за роботу на занятті. Усно:

- алгоритм знаходження найбільшого та найменшого значення на проміжку

- Рефлексія «Я знаю.... Я вмію..... Мені важко...»

8.Інструктаж заключний

9. Видача завдань для самостійної роботи:                                                  3 хв

Розд. III. ,§.18, впр. 50(1_3),стр.106