Ламана. Многокутники. Площі фігур.

Скарбничка математичних ідей

 

 

Геометрія 8 клас.

 

 

 Ламана. Многокутники.

Площі фігур.

 

Підготувала вчитель математики

Шеремет В.П.

Недостатньо мати хороший розум,

Головне – уміти його використовувати.

Рене Декарт.

 

 

Мій розумний учню!

1. Цінуй набуті знання, час, наполегливість;
2. Продемонструй грамотність у виконанні поставлених завдань;
3. Сприймай інформацію зацікавлено, вдумливо;
4. Не бійся помилятися!
5. Повір у свої сили!
6. Май гарний настрій!

На уроці як у лісі: трішки забарився – і вже пішли. Будь ласка, не загубіться. В.Шаталов.

Многокутники, зокрема трикутники і чотирикутники, - найважливіші й найпоширеніші геометричні фігури.                                                                                     Уже піфагорійці(6 ст.до н.е.) мали поняття про паралелограм та деякі його властивості.                                                    Термін «паралелограм» походить від грецьких слів «паралелос» - «той, що йде поряд» і «пряма» - «лінія». Цей термін увів Евклід.                                                                  Термін  «діагональ» походить від поєднання двох грецьких слів: «діа» - «через, крізь» і «гонія» - «кут», «той, що йде від кута до кута».                                                                 Слово «трапеція» - грецьке. Воно колись означало столик. Цей термін спочатку застосували в розумінні чотирикутника і лише у 18 ст. він набув сучасного змісту. Про те, що середня лінія трапеції дорівнює півсумі її основ, було відомо ще стародавнім єгиптянам, землемірам Вавилону (не пізніше ніж ІІ ст.. до н,е.) Форму, близьку до трапеції, мають поперечні перерізи різниз деталей, споруд, зокрема каналів, гребель тощо.

Площа многокутника – геометричне, фізичне, географічне, загальнонаукове і навіть побутове поняття. Чим більша площа квартири, тим зручніше в ній жити, тим вона дорожча; чим більша площа поля, тим більший урожай з нього можна зібрати, тим більший податок за нього треба платити.

Вправа «Занурення в тему».                                                        Пригадати основні терміни даної теми.                                      Ламана, многокутник, багатокутник, чотирикутник, периметр, площа, квадрат, прямокутник, паралелограм, ромб, середня лінія, правильний многокутник, діагональ, трапеція.

Пам'ять – вартовий усьому і скарбничка всього. Ціцерон

Вправа «Мозкова атака». Пригадай!

1. Які однакові властивості має прямокутник і квадрат?
2. Чи існує чотирикутник із трьома тупими кутами?
3. Чи правильно, що в паралелограмі сума протилежних кутів дорівнює 180⁰?
4. Чи може більший кут чотирикутника бути гострим?
5. Що таке середня лінія трапеції?
6. Чи може діагональ ромба бути вдвічі більшою від його сторони?

 

Уся математика, як наука, історично розвинулася з практики. Д.О.Граве.

***************************

 

«Без теорії немає практики!»                                                           Ламана. Многокутник.

1.              Назвіть основні елементи ламаної.
2.              Що таке периметр багатокутника?
3.              Назвіть основні елементи багатокутника. Виконайте побудову.
4.              Що таке діагональ багатокутника?
5.              Який багатокутник є правильним?
6.              Чому дорівнює сума всіх кутів опуклого багатокутника?
7.              Коли можна вписати в коло багатокутник?
8.              Коли можна описати навколо кола багатокутник?
9.              Чи може площа фігури бути від'ємним числом?
10.         Як називаються фігури, які мають рівні площі?
11.         За якою формулою знаходять площу прямокутника?
12.         За якою формулою знаходять площу трапеції?

 

Історична довідка.                                                                                Правильно обчислювали площі прямокутника, трикутника і трапеції вчені Вавилона ще 4 тисячі років тому. Архімед першим знайшов формулу для обчислення площі трикутника, яку згодом було названо формулою Герона.

 

***Одиничний квадрат – це квадрат, сторна якого дорівнює одиниці довжини.

***Дві фігури з рівними площами називаються рівновеликими.

У Київській Русі певних мір площі не існувало. Тому селяни платили податки не від площі оброблюваного грунту, а «від сохи», «від рала», «від диму», «від обжі». Обжа – це площа, які міг зорати селянин одним конем за один день. З 15 ст. ввели точнішу одиницю площі – десятину. Це – площа квадрата, сторона якого дорівнює десятій частині версти(десятина – 1,09 га). У 18 ст. українці довжини вимірювали у вершках, аршинах, сажнях, а площі визначали відповідно – у квадратних вершках, квадратних аршинах, квадратних сажнях.                                                                              1 кв.аршин=256 кв.вершків=784 кв. дюйми.                                                 В англомовних країнах і тепер площі визначають у неметричних мірах: невеликі – у квадратних дюймах, квадратних футах, а площі земельних ділянок – в акрах тощо.

1 дм=4 дюйми;   1дм²=16 кв. дюймів.

***Сума усіх кутів опуклого многокутника дорівнює 180°(n-2).

 

«ЦЕ ВАЖЛИВО!».                                                                Теоретичні відомості:

1.Площа прямокутника зі сторонами а і b обчислюється за формулою:  S=ab.

2.Площа паралелограма дорівнює  добутку його сторони на висоту, проведену до цієї сторони. S=ah.

3. Площа паралелограма дорівнює добутку його сторін на синус кута між ними. S=ab sinα.

4.Площа паралелограма дорівнює половині добутку діагоналей на синус кута між ними. S=sinα.

5.Площа ромба дорівнює половині добутку діагоналей.

6.Площа трикутника обчислюється за формулами: S=ah,  S=, 

 ФОРМУЛА ГЕРОНА:  S=,                                                               p= – півпериметр.

Для рівностороннього трикутника:  S=.

7. Площа многокутника, описаного навколо кола, дорівнює добутку півпериметра многокутника на радіус кола: S=pr.

8.  S=.

9.Площа трапеції дорівнює добутку півсуми її основ на висоту: S= h.

10 Якщо многокутник вписаний у коло – усі вершини лежать на колі.

11. Якщо многокутник описаний навколо кола – усі сторони дотикаються до кола.

12. Якщо у чотирикутника сума протилежних кутів дорівнює 180⁰, то навколо нього можна описати коло.

13. Якщо у опуклого чотирикутника суми довжин протилежних сторін рівні, то в нього можна вписати коло.

14. Площі подібних фігур відносяться як квадрати їх відповідних лінійних розмірів.

Математика – це те, за допомогою чого люди керують природою і собою. А.М.Колмогоров.

Чи правильно, що?…                                                                                 Виберіть правильне твердження:

  1)паралелограмом називається чотирикутник, у якого дві сторони паралельні;                                                                                                   2)у паралелограма всі кути можуть бути гострими;                                                                           3)існує паралелограм, у якого лише один кут тупий;                                                  4)паралелограм може мати три рівні кути;

5)якщо в паралелограма діагоналі рівні, то він є прямокутником;                                                                   6)прямокутник, вписаний у коло, є квадратом;                                                                                                         7)якщо в ромба діагоналі перетинаються під прямим кутом, то він є квадратом;                                                                                                                8)якщо в трапецію можна вписати коло, то вона рівнобічна;                                                                                                     9)у паралелограма діагоналі рівні і є бісектрисами його кутів;                                                                                      10)діагоналі прямокутника рівні;                                                                                             11)діагоналі квадрата рівні.

Учитися міркувати – це значить розвивати вміння із мінімуму фактів здобувати максимум інформації.                        А. Ейнштейн.

************************************************************

Вправа на виділення загальних і суттєвих властивостей понять.

• Назвіть усі вам відомі властивості паралелограма. Які властивості з усіх чотирикутників належать тільки паралелограму.
• Назвіть не менше ніж 12 властивостей квадрата.
• Назвіть властивості, що належать усім прямокутникам.
• Назвіть загальні властивості трапеції і ромба.
• Укажіть спільні властивості для прямокутника і ромба.

Жодна інша наука не навчає так ясно розуміти гармонію природи, як математика…П.Карус.

 

 

Вправа «Мозкова атака».                                                              Розв’язати задачі.

1. Знайти площу прямокутника, якщо його сторони дорівнюють       8 см і 5 см.
2. Площа квадрата дорівнює 12 см². Чому дорівнює його сторона?
3. Одна зі сторін прямокутника на 3 см більша, ніж інша, а його площа дорівнює 154 см². Знайти сторони прямокутника.
4. Сторона паралелограма дорівнює 16 см, а висота проведена до неї – 5 см. Знайти площу паралелограма.
5. Обчислити периметр ромба, якщо його висота дорівнює    4 дм, а площа – 36 дм².
6. Сторони паралелограма дорівнюють 10 см і                     4 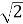см, а кут між ними 45⁰. Обчислити площу паралелограма.
7. Знайти площу ромба, якщо його діагоналі дорівнюють   10 см і 12 см.
8. Обчислити площу трикутника зі сторонами                        13 см, 20 см,     21 см.
9. Обчислити площу трикутника, якщо відомі сторона, що дорівнює 17 см і висота, проведена до неї – 5 см.
10.                     Обчислити площу рівнобедреного трикутника, якщо бічна сторона дорівнює 5 см, а основа – 6 см.
11.                     Знайти площу трапеції з основами 19 см і 21 см і висотою 14 см.
12.                     Обчислити площу трикутника зі сторонами 4 см, 5 см і 7 см.
13.                     Обчислити радіус кола, описаного навколо трикутника зі сторонами 13 см, 14 см і 15 см.
14.                     Обчислити радіус кола, вписаного в трикутник зі сторонами 6 см, 25 см, 29 см.
15.                     Середня лінія трапеції – 7 см, а висота –                                  11 см. Знайти площу трапеції.
16.                     Знайти кути опуклого многокутника, якщо вони пропорційні числам 1,3,5,7,11.
17.                     Визначити суму внутрішніх кутів опуклого семикутника.
18.                     Скільки сторін має многокутник, якщо сума його внутрішніх кутів дорівнює 1980⁰?
19.                     Два кути опуклого многокутника дорівнюють по 100⁰. Скільки вершин має цей многокутник?
20.                     Знайти площу трикутника, основа якого дорівнює 12 см, а висота –  5 см.
21.                     Знайти висоту трикутника, основа якого дорівнює 35 см, а площа – 175 см².
22.                     Знайти площу прямокутного трикутника, катети якого дорівнюють 6 см і 12 см.

***********************************************

Математику слід вивчати у школі ще й із тією метою, щоб одержані тут знання були достатні для звичайних потреб у житті.                                                              М.І. Лобачевський.

**********************************

 Площі фігур. Завдання для самостійної роботи. Трапеція. Трикутник.

1. Основи трапеції 6,7 см і 4,3 см, а висота 0,8 см. Знайти площу трапеції.
2. Середня лінія трапеції – 9 см, а висота – 13 см. Знайти площу трапеції.
3. У прямокутній трапеції менша бічна сторона 24 см, більша діагональ є бісектрисою гострого кута в 60˚. Обчислити площу трапеції.
4. Площа трапеції 192 см², а висота – 16 см. Знайти основи трапеції, якщо одна з них у 3 рази більше другої.
5. Основи рівнобічної трапеції дорівнюють 50 і 14 см, а діагональ дорівнює 40 см. Обчисліть площу трапеції.
6. Основи рівнобічної трапеції дорівнюють 50 і 30 см, а бічна сторона дорівнює 26 см. Обчисліть площу трапеції.
7. Периметр рівнобедреного трикутника дорівнює                      80 см, а бічна сторона – 25 см. Обчисліть площу трикутника.
8. Периметр рівнобедреного трикутника 80 см, а основа –     30 см. Обчисліть площу трикутника.
9. Бічна сторона і основа рівнобедреного трикутника відносяться, як 5:6. Обчисліть площу трикутника, якщо висота, проведена до основи, дорівнює 24 см.
10. Катети прямокутного трикутника відносяться, як 3:4, а гіпотенуза дорівнює 25 см. Обчисліть площу трикутника.
11. Гіпотенуза і катет прямокутного трикутника відносяться, як 5:6, а другий катет дорівнює 15 см. Обчисліть площу трикутника.
12. Різниця катетів прямокутного трикутника дорівнює 2 см, а гіпотенуза – 10 см. Обчисліть площу трикутника.
13. Сторони трикутника дорівнюють 13, 14 і 15 см. Обчисліть площу трикутника.
14. Сторони трикутника дорівнюють 15, 26 і 37 см. Обчисліть площу трикутника.
15. Дві сторони трикутника дорівнюють 25 і 40 см, а висота, опущена на третю сторону, дорівнює 24 см. Обчисліть площу трикутника.

Розв´язування задач є найхарактернішим і специфічним різновидом вільного мислення. В.Джеймс.

********************************

 

 ЦЕ ЦІКАВО!                                                                                                                         Як відомо, бджолині стільники мають форму правильного шестикутника. Отже, бджоли знають математику? Учені, які досліджували бджолині стільники, переконалися: всі кути, що утворює шестикутник бджолиної чарунки, саме такі, для яких чарунка найбільш містка, і при цьому на неї йде найменше воску. Начебто бджоли, будуючи свої стільники, користуються складними математичними обчисленнями. Побудовані ними без усяких креслень стільники з найбільшою точністю відтворили розміри ідеальної споруди, розрахованої за всіма правилами науки. Виконувати складні завдання і знаходити вихід зі складної ситуації можуть не лише бджоли, а й інші істоти. Так, що це таке? Знання математики? Учені дійшли висновку, що це не що інше, як вироблений у процесі еволюції інстинкт.                                                                 Інстинкт – природна здатність виконувати необхідні для життя дії – от що дає можливість бобру будувати прекрасні дамби, а голубу знаходити дорогу додому. Інстинкт – це вроджені програми поведінки, для здійснення яких майже не потрібно попереднього навчання. Існує версія, що відстань між кутами шестикутника визначається розмірами самої бджоли. Як було виявлено в результаті спостережень, бджола після польоту приземляється на шість точок, що можуть бути вершинами фігури.  Бджоли, не знаючи математики, «визначили», що правильний шестикутник має найменший периметр порівняно з периметрами правильних трикутників і квадратів. Будуючи шестикутні чарунки, бджоли витрачають менше воску на їх побудову й ощадливо використовують площу всередині невеликого вулика.

******Установіть відповідність між площами многокутників(1-4) та їх числовими значеннями(А-Д).

1.	У прямокутному трикутнику один з катетів дорівнює 12 см, медіана, проведена до гіпотенузи, дорівнює 10 см. Знайдіть площу трикутника.	А	120 см²
2.	Сторона ромба дорівнює 13 см, одна з діагоналей – 24 см. Знайдіть площу ромба.	Б	60 см²
3.	У рівнобедреному трикутнику бічна сторона дорівнює 13 см, основа – 10 см. Знайдіть площу трикутника.	В	96 см²
4.	Обчисліть площу рівнобічної трапеції, основи якої дорівнюють 7 см і 11 см, одна із кутів при основі трапеції дорівнює 45°.	Г	240 см²
		Д	18 см²
1.	У рівнобедреному трикутнику висота, проведена до основи, дорівнює 12 см, бічна сторона – 13 см. Знайдіть площу трикутника.	А	120 см
2.	Бічна сторона рівнобічної трапеції дорівнює 10 см, її основи – 12 см і 28 см. Знайдіть площу трапеції.	Б	60 см²
3.	Сторона ромба дорівнює 17 см, одна з діагоналей – 16 см. Знайдіть площу ромба.	В	54 см²
4.	Чому дорівнює площа прямокутного трикутника з катетом 12 см і гіпотенузою                   15 см?	Г	240 см²
		Д	140 см²

 

Вправа «Термінологічне завдання».

1. Геометрична фігура, що складається з відрізків, називається….
2. Ламана, що не має самоперетинів, називається….
3. Сума довжин усіх сторін ламаної, називається….
4. Якщо кінці ламаної збігаються, то вона називається….
5. До основних елементів многокутника відносять….
6. Відрізок, що сполучає дві несусідні вершини, називається…
7. Сума кутів опуклого многокутника, дорівнює….
8. Діагоналей у прямокутника….
9. Сторони прямокутного трикутника, називаються….
10.      Основні види чотирикутників:…..
11.      У квадрата усі кути….

 

Геометрія кладе в основу чисте споглядання простору. І. Кант.

*********************************

Контрольна робота. Варіант І.

1. В опуклому багатокутнику сума його внутрішніх кутів дорівнює 1440˚. Знайдіть кількість його сторін.
2. Знайдіть площу квадрата зі стороною 3,5 см.
3. У паралелограмі АВСД кут А дорівнює 30˚, а його бісектриса ділить сторону ВС на відрізки 7 см і                                    2 см, рахуючи від вершини тупого кута. Знайдіть площу паралелограма.
4. В трикутнику АВС кут С дорівнює 45˚, АВ=10 см, висота АД ділить сторону СВ на відрізки СД=8 см і ДВ=6 см. Знайдіть площу трикутника і висоту, проведену до сторони АВ.

 

 

Контрольна робота. Варіант ІІ. Многокутники.

1. Знайти радіус кола,вписаного в правильний многокутник зі стороною 30 см, якщо радіус кола, описаного навколо цього многокутника, дорівнює 10 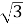см.
2. Довжина хорди 6 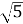см. Знайти довжину дуги цієї хорди, якщо градусна міра дуги дорівнює 60.
3. Ламана складається з чотирьох ланок, довжини яких відносяться як 2:5:4:8. Довжина ламаної                        152 см. Визначити довжину кожної ланки.

Історична довідка.                                                                                   Кожний многокутник можна розбити на трикутники, тоді легко знайти площу многокутника як суму площ складових трикутників. Так  і робили єгипетські землеміри, визначаючи площі ділянок після розливу р.Нілу, а знаходити площу трикутника єгиптяни вміли вже кілька тисячоліть тому.

***Якщо відповідні сторони подібних трикутників відносяться як а:в, то їх площі відносяться як а²:в².

Практична робота:

1.Як визначити розміри прямокутної ділянки, всі вершини якої недоступні?

2. З фанери випиляли квадрат. Як перевірити, чи одержаний чотирикутник справді є квадратом?

3.Клаптик паперу має форму трапеції, один із тупих кутів якої відірвано. Як знайти довжини її сторін?

4. Поділити ділянку землі, яка має форму прямокутної трапеції на рівновеликі частини. Скільки розв´язків має задача?

5.У Стародавньому Єгипті площу рівнобедреного трикутника обчислювали як добуток бічної сторони на половину основи. Визначити процент похибки, який допускали єгиптяни, обчислюючи площу рівнобедреного трикутника з основою 18 см і бічною стороною 15 см.

6. Виріжте з паперу п´ятикутник з периметром 25 см, який є водночас вписаним у коло і описаним навколо кола.

7.Визначте, скільки рулонів шпалер потрібно придбати, щоб обклеїти ним вашу кімнату. Довжина рулона 10 м, ширина 0,5 м.

8.Намалюйте квадрат, сторона якого дорівнює 4 см. Поділіть його на 12 рівних трикутників і 4 рівні квадрати. Знайдіть площі утворених квадратів і трикутників.

9. Підлога шкільної актової зали має форму прямокутника розміром 11 м на 8,8 м. Підлогу потрібно встелити плитками квадратної форми розміром 22 см на 22 см кожна. Скільки потрібно таких плиток, якщо на обрізання та підгонку витрачають 3% від загальної площі всіх плиток?

 

Література:

1. Погорелов А.В. Геометрия 7-9 кл. – К.:Школяр, 2003.
2. Роева Т.Г.,Синельник Л.Я.,Кононенко С.А.                                                                           Геометрия в таблицях 7-9 кл., - Х.: Гимназия, 2001.
3. Журнал «Математика в школах України».