Методичні рекомендації застосування інформаційно-комунікаційних технологій навчання при викладанні математики на прикладі теми "Комплексні числа"

Тема: Комплексні числа.

 

Мета: ознайомити студентів з поняттям комплексного числа, необхідністю його введення в математику, показати три форми (тригонометричну, алгебраїчну та показникову) комплексного числа, вивчити основні поняття та означення, дії над комплексними числами, ознайомити з геометричною інтерпретацією комплексного числа.

Тип заняття: лекція.

План.

1.               Поняття комплексного числа. Необхідність розширення класу чисел. Визначення комплексного числа.
2.               Алгебраїчна форма комплексного числа. Дії над комплексними числами в алгебраїчній формі. Геометрична інтерпретація комплексного числа, суми та різниці комплексних чисел. Розв’язування квадратних рівнянь з від’ємним дискримінантом.
3.               Тригонометрична форма комплексного числа. Перехід від алгебраїчної форми до геометричної і навпаки. Модуль комплексного числа. Дії над комплексними числами, заданими в тригонометричнїй формі.
4.               Показникова форма комплексного числа.

 

1.Постановка проблемного запитання.

Чи існує корінь квадратний з від’ємного числа?

Потреби алгебри вимагають такого розширення поняття числа, при якому здійснюється дія добування корення з від’ємного числа. З розширенням поняття числа ми вже неодноразово зустрічалися. Для того, щоб зробити ділення одного дійсного числа на інше, ввели дробові числа, для можливості віднімання більшого числа з меньшого ввели від'ємні числа, для того щоб мати можливістьзаписати результати вимірювання відрізка несумісного з одиницею вимірювання знадобилися іраціональні числа. Приєднання кожного наступного классу числа до попереднього розширює поняття числа і разом з тим розширює сферу використання данного поняття. Добування кореня парного степеня з від'ємного числа вимагає розширення множин дійсних чисел.

 

називається уявною одиницею. Числа, що містять уявну одиницю називаються уявними числами. Приклад: 2і, -5і, .

Комплексні числа виникли в математиці на початку XVI століття у зв'язку з рішенням алгебраїчних рівнянь 3-го ступеня, а пізніше, і рівнянь 2-го ступеня. Деякі італійські математики того часу (- Сципіон дель Ферро, Ніколо Тарталья, Джіроломо Кардано, Рафаель Бомбеллі) ввели в розгляд символ √ -1 як формальне рішення рівняння х 2 +1 = 0, а також вираз більш загального вигляду (а + b ∙ √ -1) для запису рішення рівняння (х-а) 2 + b 2 = 0. Згодом вирази виду (а + b ∙ √ -1) стали називати «уявними», а потім «комплексними» числами і записувати їх у вигляді (а + bi) (символ i для позначення √ -1 ввів Леонард Ейлер у XVIII ст.) . Цих чисел, чисел нової природи виявилося достатньо для вирішення будь-якого квадратного рівняння (включаючи випадок D <0), а також рівняння 3-ей і 4-го ступеня.

Математики XVI ст. і наступних поколінь аж до початку XIX сторіччя ставилися до комплексних числах з явним недовір'ям і упередженням. Вони вважали ці числа «уявними» (Декарт), «неіснуючими», «вигаданими», «виникли від надлишкового мудрування» (Кардано) ... Лейбніц називав ці числа «витонченим і чудовим притулком божественного духу», а √ -1 вважав символом потойбічного світу (і навіть заповідав накреслити його на своїй могилі).

Проте використання апарату комплексних чисел (незважаючи на підозріле ставлення до них), дозволило вирішити багато важкі завдання. Тому з часом комплексні числа займали все більш важливе положення в математиці і її додатках. В першу чергу вони глибоко проникали в теорію алгебраїчних рівнянь, істотно спростивши їх вивчення.

Після того, як в XIX ст з'явилося наочне геометричне зображення комплексних чисел за допомогою точок площини і векторів на площині (Гаус в 1831 р, Вессель в 1799 р, Арган в 1806 р), стало можливим зводити до комплексних числах і рівнянням для них багато завдань природознавства , особливо гідро-і аеродинаміки, електротехніки, теорії пружності і міцності, а також геодезії і картографії. З цього часу існування «уявних», або комплексних чисел стало загальновизнаним фактом і вони отримали таку ж реальний зміст, як і числа дійсні. До теперішнього часу вивчення комплексних чисел розвинулося в найважливіший розділ сучасної математики - теорію функцій комплексного змінного (ТФКЗ).

Логічно строгу теорію комплексних чисел побудував у XIX ст (1835 р) ірландський математик Вільям Роумен Гамільтон.

У багатьох розділах математики та її застосуваннях неможливо обмежитись розглядом лише дійсних чисел. Вже досить давно під час розв’язування різних задач виникла потреба добувати квадратний корінь з від’ємних чисел. Щоб ця дія стала можливою, ввели множину нових чисел.

Без комплексних чисел неможливо розв'язати безліч цікавих та непростих на перший погляд задач з механіки, фізики, математики, термодинаміки. Вони доповнюють множину дійсних чисел, використовуючи при цьому власні правила обчислень сум, часток і т.д.

Означення 1. Комплексним числом називають сукупність дійсного числа і уявного числа z = a+bi, де а - дійсна частина комплексного числа, bi – уявна частина комплексного числа, b – коефіцієнт при уявній частині , і – уявна частина.

позначаються символами Re z і Im z відповідно (real - дійсний, imanginerum - уявний).

Приклад:

Комплексні числа a+bi, в яких називаються уявними числами, а числа виду 0+bi, – чисто уявними числами. Множина комплексних чисел позначається C .

2. Запис комплексного числа z у вигляді суми двох чисел – дійсного числа а і чисто уявного числа bi, тобто у вигляді a+bi, називається алгебраїчною формою комплексного числа.

Операції над комплексними числами, записаними в алгебріїчній формі, виконуються таким же чином, як і над звичайними многочленами, з заміною на -1.

Означення 2. Комплексні числа називаються рівними тоді і тільки тоді , коли a=b i c=d.

Означення 3. Сумою комплексних чисел називається комплексне число (a+c)+(b+d)i, тобто

z₁+z₂ =(a+b)+(ci+di)=(a+c)+(b+d)i

Наприклад: знайти суму комплексних чисел

z₁+z₂=(2-1)+((-1)i+3i)=(2-1)+(-1+3)i=1+2i

Додавання комплексних чисел має властивості:

- комутативності z₁+z₂=z₂+z₁

- асоціативності z₁(z₂z₃)=(z₁z₂)z₃

- дистрибутивності z₁(z₂+z₃)=z₁z₂+z₁z₃

Для   будь-яких m i n мають місце рівності:

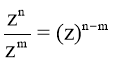
Наприклад : обчислити z^-3 , якщо z=1+i.

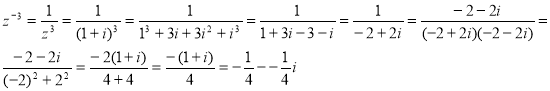
Геометрична інтерпретація :

Будь-яке комплексне число виду a+bi геометрично зображається точкою на координатній площині з координатами A(a;b) або як вектор з початком в точці (0,0) і кінцем в точці А з координатами (a;b).

в

 

  

 

    

О     а

Площина , точкам якої у відповідність поставлені комплексні числа , називається комплексною площиною . Вісь абсцис називається дійсною віссю ,а вісь ординат – уявною віссю комплексної площини.

 

Геометричне зображення суми комплексних чисел.

 Нехай дані комплексні числа z1=a+bi i z2=c+di і відповідні їм вектори i . На векторах i будується паралелограм ОАDB.

Тоді +=.

 

 

 

 

 

 

 

 

 

 

Означення 5.Різницею комплексних чисел z₁=a+bi i z₂=c+di називають число z=x+yi  , яке задовольняє рівності z₂+z=z₁.

z₁-z₂=(a+bi)=(a-c)+(b-d)i=x+iy=z

Наприклад : Знайти різницю комплексних чисел z₁=4+5i i  z₂=(-2)+3i

Комплексне число 0+0і називається нулем .

 Z є С: z+0=z   і       z*0=0      

Означення 6. Числа Виду – a-bi , a+bi називається протилежними комплексними числами .

Наприклад : 3+5і  і  -3-5і.

Означення 7. Числа виду a+bi i a-bi , які відрізняються знаками перед уявними частинами називаються спряженими комплексними числами .

Наприклад : -7 +2і і -7-2і.

Означення 8. Часткою комплексних чисел z₁=a+bi i z₂=c+di ≠0

Називається комплексне число z=x+yi , якому задовольняє рівність 

z_2* z=z₁  .

 

 

Розглянемо частку:

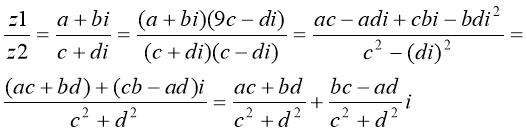
Для того , що б позбутися уявного числа в знаменнику , чисельник і знаменник домножають на число , спряжене до знаменника.

Наприклад :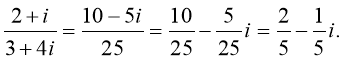

   Означення 9.Число ,де z0 позначається і називається оберненим до числа z.

  

,

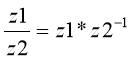
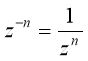
Приклад: Обчислити число, обернене до числа

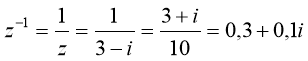
Таким чином сума комплексних чисел геометрично зображається сумою відповідних векторів , яка знаходиться за правилом паралелограма.

Геометричне зображення різних комплексних чисел.Нехай дано число . Тоді число геометрично зображається точкою, симетричною відносно початку координат до точки , що відповідає числу .

 

 

` 

 

 

 

 

 

 

 

 

 

Відмітимо , що взаємно спряжені комплексні числа і Зображуються на площині точками або векторами , симетричними відносно дійсної осі.

       Таким чином сума комплексних чисел геометрично зображається сумою відповідальних векторів, яка знаходиться за правилом паралелограма.

     Геометричне зображення різних комплексних чисел. Нехай дано число z=a+bi. Тоді число –z=-a-bi геометрично зображається точкою, симетрично відносно початку координат до точки, що відповідає числу z=a+bi.

     z₁-z₂=(a+bi)-(c+di)=z₁+(-z₂)

     z₁=a+bi

     z₂=c+di

 

 

 

 

-(c+di)

     Відмітимо, що взаємно спряжені комплексні числа z=a+bi і =a-bi

Зображуються на площині точками або векторами, симетрично відносно дійсної осі.

  

 

 3. Означення 10. Модулем комплексного числа z=a+bi 

         називається довжина (модуль) відповідного йому вектора.

Модуль комплексного числа позначається |z|=r. З означення випливає, що

z: |z|≥0 і |z|=0 → z=0.

 

За теоремою Піфагора: |z|=.

 

 

 

 

 

 

Приклад: Знайти модуль комплексного числа: z=4-3i.

|z|===5

      Якщо r – деяке додатнє дійсне число, то за означенням модуля комплексного числа отримуємо
      а) множина всіх чисел z, для яких |z|=r, є коло з радіусом r і з центром в (0;0).

     б) множина всіх чисел z, для яких |z|≤r, є круг з радіусом r і з центром в (0;0).

   в) множина всіх чисел z, для яких |z|>r, є зовнішня частина круга з радіусом r і з центром в (0;0).

Приклад:

Зобразити на комплексній площині області, що задаються умовами: |z|=5.

 

 

 

 

Означення 11. Аргументом комплексного числа z≠0 називається величина бідь-якого направленого кута, утвореного додатнім напрямком дійсної осі і вектором, що відповідає числу z.

При цьому значення аргумента додатнє, якщо кут направлений проти руху год. стрілки і від`ємний в протилежному випадку.

Аргумент числа z позначається символом argz або µ=arg z. Аргумент визначається неоднозначно. В якості аргумента можна взяти будь-яке з чисел µ+2πк, де к – будь-яке ціле число. Як правило, через аргумент argz позначається найменше додатнє чи найменше за модулем значення аргумента.

         Якщо =arg z, z=a+bi, то cos =a/r, sin =b/r. Звідки маємо: a=rcos , b=rsin . За допомогою цих формул можна перейти від алгебраїчної форми комплексного числа до нового запису комплексного числа.

 Z=a+bi=rcos +irsin =r(cos +isin ).

Означення 12. Вираз r(cos +isin ) називається тригонометричною формою комплексного числа.

Приклад: Записати числа в тригонометричній формі

 

 

 

 

 

Дії над комплексними числами, заданими в тригонометричній формі.

1. Множення.

2. Піднесення до степеня

– Формула Муавра.

Приклад:

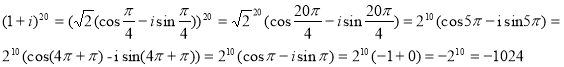
3. Ділення.

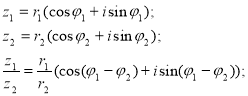
Приклад:

 

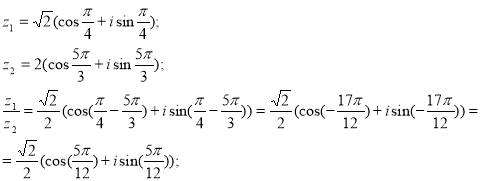
4. Добування кореня комплексного числа.

Означення 13. Коренем nо степеня, , , з числа z називається комплексне число U, для якого .

Теорема. операція добування корення n-го степеня, , з числа z завжди можлива і має n різних значень.

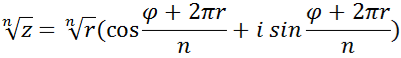
Приклад.

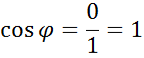
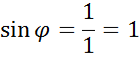
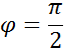
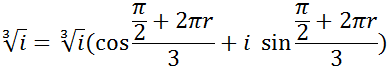
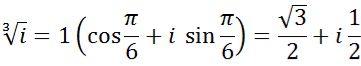
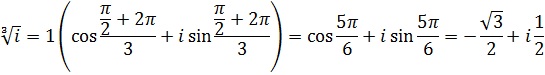
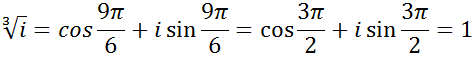
4. Крім алгебраїчної і тригонометричної є ще показникова форма запису комлпексних чисел. Розглянемо комплексні числа виду

Нехай    

Знайдемо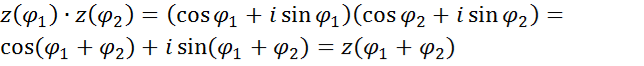

Продиференціюємо

Введемо в розгляд комплексний показниковий вираз , де – число Ейлера.

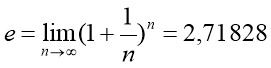
дійсне число.

Введемо функцію комплексних змін .  Для неї мають місця звичайні правила множення і  диференціювання:

Значить , кожному комплексному числу можна поставити у відповідність комплексний показників вираз .

- форма Ейлера.

Нехай дано комплексне число Роблячи заміну маємо .

Означення 14.Вираз виду називається показниковою формою комплексного числа.

Показникова форма комплексного числа зручна для виконання операцій над комплексними числами.

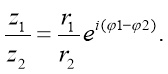
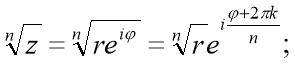
Приклади :

 Знайти показникові форму чисел.

 

 

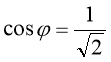
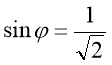
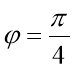
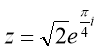
Підведення підсумків заняття.