Лекція "Основні поняття кінематики. Кінематична точка. Види руху точки в залежності від швидкості та прискорення. Просторі рухи твердого тіла. Сила інерції. Метод кінетостатики"

Лекція з дисципліни

«Технічна механіка»

273 Залізничний транспорт

Галузь знань 27 «Транспорт»

освітньо-кваліфікаційний  рівень молодший спеціаліст

для студентів заочної форми навчання

Дисципліна: Технічна механіка

Блок МПН.08.01 Види напруженого стану деталей

Модуль ПФ.С.ОЗ.Р.03.10-2 Види напруженого стану деталей (Кінематика та динаміка)

Тема: Основні поняття кінематики. Кінематична точка. Види руху точки в залежності від швидкості та прискорення. Просторі рухи твердого тіла. Сила інерції. Метод кінетостатики.

План  лекції:

1 Основні поняття кінематики.

2 Кінематика твердого тіла

Основні поняття кінематики. Кінематика точки.

Основним завданням кінематики є вивчення загальних законів руху матеріальних точок і твердих тіл без урахування причин, що їх викликають. Кінематика відповідає на питання: як рухається тіло.

1 Механічний рух - це зміна покладено ід тіла в просторі відносно інших тіл з плином часу.

Будь-яке механічне рух характеризується наступними параметрами:

• Траєкторія руху - це лінія, уздовж якої рухається тіло. В залежно від траєкторії рух може бути прямолінійним і криволінійним

• Шлях s - це відстань, пройдену тілом уздовж лінії траєкторії (рисунок 1)

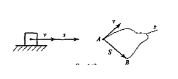
Рисунок 1 –Механічний рух

• Переміщення S- це спрямований відрізок прямої, що сполучає початкове і кінцеве положення тіла ( рисунок 1).

• Швидкість v - це величина, що характеризує швидкість зміни пройденого шляху за одиницю часу (похідна d шляху по часу):

V = ds/ dt, м/с ,  Vcр = S/t

• Дотичне прискорення аτ це величина, яка характеризує швидкість зміни

величини швидкості за одиницю часу:

аτ = dv/dt, м/с²,    аτ= v-v0/t

Дотичне прискорення завжди спрямоване по лінії вектора швидкості (рисунок 2)

•

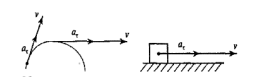
Рисунок 2-Дотичне прикосання

Нормальне прискорення аn - це величина, яка характеризує зміну напрямку вектора швидкості:

аn =v² /r

де  р- радіус кривизни траєкторії.

Нормальне прискорення завжди спрямоване по радіусу до центру кривизни траєкторії (рисунок 3).

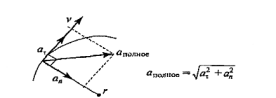
Рисунок 3-Нормальне прикосання

Види руху точки в залежності від прискорення:

1) рівномірний - це рух точки з постійною за величиною швидкістю. характеризується

наступними величинами:

v —s/t - const; s = vl; aτ = 0; аn = v² /r

2) рівноперемінне (рівноускорене, рівнозамідленне) - це рух точки з постійним

дотичним прискоренням. Характеризується такими величинами :

/ aτ/ = const; аτ= v-v0/t; аn = v² /r; v= v0+ аτ · t; s = v0 t+ aτ t²/2; s = v²- v0 /2 аτ

Кінематика твердого тіла

1 Найпростіші рухи твердого тіла

До простих рухів твердого тіла відноситься поступальний і обертальний рух.

Поступальний рух твердого тіла - це такий рух, при якому пряма, проведена в тілі між будь-якими двома точками, переміщається паралельно самій собі.

При поступальному русі всі точки тіла мають однакові швидкості, однакові прискорення і проходять однакові відрізки шляху (рисунок 4).

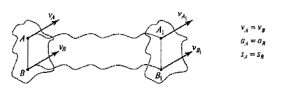
Рисунок 4-Поступальний рух

Робота більшості машин і механізмів заснована на обертальному русі.

2 Обертальним рухом твердого тіла навколо нерухомої осі називається такий рух, при якому всі точки тіла рухаються по колах, які лежать в площинах, перпендикулярних осі обертання, з центрами на цій осі.

Будь-яке обертальний рух характеризується наступними параметрами (рисунок 5):

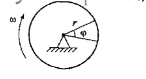
Рисунок 5-Обертальний рух

1. φ , рад- кут повороту, або кутове переміщення ( 1 рад= 57,3˚);

     2)ω=  φ/ t - кутова швидкість (характеризує зміну вугілля повороту за одиницю    часу).

Середня кутова швидкість

ω ср = φ/ t

Кутове прискорення - це величина, яка характеризує зміну кутової швидкості за

одиницю часу:

ε = (ω – ω0 )/ t

Види обертального руху твердого тіла в залежності від прискорення:

1) рівномірний - це рух тіла з постійною кутовою швидкістю:

ω=  φ/ t = const,  φ = ω t,  ε =0

Лінійні швидкості і прискорення точок рівномірно обертового тіла (рисунок 6) визначається за формулою

V = ω r,  аτ=0,  аn = ω ² r

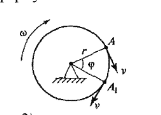
Рисунок 6- Обертальний рух

2) рівноперемене - це рух з постійним кутовим прискоренням:

ε = (ω – ω0 )/ t = const;

φ = ωи t+ ε t² / 2

ω= ωи + ε t

Контрольні питання:

1 Дати пояснення механічному руху.

2 Назвати найпростіші рухи твердого тіла

3 Дати пояснення обертальному руху твердого тіла

4 Види обертального руху твердого тіла

Література:

1М.С. Мовнин, А.Б. Йзраелит, А.Г. Рубашкін «Основи технічної механіки», с 134-153