Рівняння із двома змінними та його розв'язок

Тема. Рівняння із двома змінними та його розв'язок

Мета: сформувати уявлення про рівняння із двома змінними та його розв'язки; усвідомити зміст поняття «графік рівняння із двома змінними»; виробити вміння: відбирати перевіркою розв'язки рівняння із двома змін­ними; працювати з готовим графіком рівняння із двома змінними; пере­творювати рівняння виду у = f(x) та обчислювати розв'язки рівняння із двома змінними.

Тип уроку: засвоєння нових знань.

Хід уроку

I. Організаційний момент

II. Перевірка домашнього завдання

 Учитель збирає зошити, щоб перевірити якість корекційної роботи учнів та творче завдання.

III. Актуалізація опорних знань

Виконання усних вправ

1. Розв'яжіть рівняння:

3х = 6; 3х + 2 = 6; 6х = 3; 6 + х = 3; 6 + x = 2x – x + 6, 3х + 5 = 3х + 7.

Що означає «розв'язати рівняння»?

2. Складіть рівняння за умовою задачі:

1. довжина прямокутника х, ширина 3 м, а периметр 20 м;
2. ширина прямокутника х, довжина на 4 м більша, а периметр 20 м;
3. ширина прямокутника х, довжина у м, а периметр 20 м.

Якщо можна, розв'яжіть рівняння, знайдіть довжини сторін прямо­кутника.

3. Чи належить графіку функції у = 3х + 2 точка А(1; -5); В(3;11); С(0; 2)? Чому?
4. Чи є дана рівність правильною: 2 · 1 + 3 · (-1) = 5; 2 · 0,5 + 3 · (-1) = -2?

IV. Формулювання мети й завдань уроку

Після повторення основних понять, вивчених у темі «Лінійні рівняння з однією змінною», та виконання усних вправ і складання рівнянь разом з учнями формулюємо мету: познайомитись із тим новим видом рівняння, що зустрівся нам під час розв'язування одного із завдань.

V. Вивчення нового матеріалу

 Нове поняття «рівняння з двома змінними» вводиться на прикладах (так само, як і «рівняння з однією змінною»), а потім формулюється означення рівняння з двома змінними та означення розв'язку тако­го рівняння як впорядкованої пари чисел — значень змінних, що перетворюють рівняння на правильну рівність, так само, як і корінь рівняння з однією змінною. Це означення повинно бути добре зро­зумілим усім учням. Поняття рівносильних рівнянь із двома змінними будується на відомих учням поняттях рівносильних рівнянь та властивостях рівносильних рівнянь. І взагалі, автор вва­жає, що формування нових знань учнів буде більш результативним, а знання — більш свідомими, якщо під час вивчення нового ма­теріалу звернутись до прийому аналогії (рівняння з однією зміною). З цього випадає лише поняття графіка рівняння з однією змінною, але це є винятком, що підтверджує справедливість правила. Тому й записи в зошитах учнів можуть мати вигляд порівняльної таб­лиці, в якій виділено ключові слова.

VI. Закріплення матеріалу. Вироблення вмінь

Виконання усних вправ

1. Чи є розв'язком рівняння х – 2у = 6 пара чисел (0; 0); (2; -2); (8; 1); (0; 3); (15; 4); (6; 0); (5; -5,5)?
2. Точки А(...; 0); В(0; ...); С(1; ...); D(...; -3) належать графіку рівняння     

3х – у = 6. Знайдіть пропущені координати.

3. Виразіть змінну у через змінну х (зведіть рівняння до вигляду y = f(x)) шляхом виконання тотожних перетворень: х + у = 1; 5х + 5у = 0;

х – у = 2. За утвореною формулою знайдіть два розв'язки кожного рівняння.

Виконання письмових вправ

1. Пари значень х та у внесено в таблицю. Які з них є розв'язками рівняння 1) х² + у² = 25; 2) х² – у²=7?

2. Виразіть із рівняння змінну у через змінну х. Використовуючи утворену формулу, знайдіть три будь-які розв'язки рівняння:

1) х + у = 27; 2) 2х – у = 4,5; 3) 3х + 2у = 12; 4) 5у – 2х = 1.

3. Які з точок А(-2; -5); В(4; 1); С(1; -4); D(2; 2) належать графіку рівняння х² – 2ху + у³ = 0?
4. Доведіть, що рівняння:

1. х² + у² = -1 не має розв'язків;
2. х² + у² = 0 має тільки один розв'язок.

Додатково. Серед розв'язків рівняння х + 2у = 18 знайдіть таку пару, яка б складалась із двох однакових чисел.

VII. Підсумки уроку

Контрольні запитання

1. Що називається розв'язком рівняння з двома змінними? Чи є пара (2; 1)
   розв'язком рівнянь:

2у – х² = -2; 3х – у = 4; х² – у³ = 3; ху = 3?

2. Які рівняння з двома змінними називають рівносильними? Наведіть приклад.
3. Що таке графік рівняння з двома змінними?

VIII. Домашнє завдання

№ 1. Вивчіть зміст основних понять та складіть алгоритми:

а) «Як перевірити, чи є пара (х;у) розв'язком рівняння з двома змін­ними»;

б) «Як знайти розв'язки рівняння з двома змінними».

№ 2. Виразивши змінну у через х, знайдіть три будь-які розв'язки рівняння:

1) ху – 12 = 0; 2) 3х – у = 10.

№ 3. Які з точок А(-3; 12); В(2; -1); С(0; 3) належать графіку рівняння

х² – у + 3 = 0?

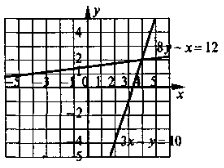
№ 4. На рисунку побудовані графіки рівнянь 3х – у = 10 і 8у – х = 12. Для кож­ного з рівнянь знайдіть за його гра­фіком декілька розв'язків. Використо­вуючи рисунок, укажіть таку пару чисел, яка є розв'язком як першого, так і дру­гого рівняння, перевірте відповідь об­численням.