Лінійне рівняння з двома змінними та його графік
Тема. Лінійне рівняння з двома змінними та його графік
Мета: формувати свідоме розуміння означення лінійного рівняння з двома змінними та вигляду графіка лінійного рівняння з двома змінними (зокрема, його особливих видів); виробляти вміння: відрізняти лінійне рівняння з двома змінними з-поміж інших рівнянь; будувати графіки лінійних рівнянь із двома змінними; подальше вдосконалювати вміння виконувати рівносильні перетворення рівнянь із двома змінними.
Тип уроку: засвоєння знань, умінь та навичок.
Хід уроку
I. Організаційний момент
II. Перевірка домашнього завдання
Під час самоперевірки за зразком з'ясовуємо основні моменти в розв'язаннях завдань № 2; 3; 4.
Бажаючі учні готують презентацію складених ними алгоритмів. Після презентації проводиться перевірка та корекція.
III. Формулювання мети й завдань уроку
Можна залучати до цього учнів, якщо звернутись до спостережень, що були здійснені у ході виконання № 4 з домашнього завдання, а саме: рівняння із двома змінними мають дуже схожий вигляд (як описати його?), графіки їх рівнянь також мають однаковий вид — прямі (ми знаємо, що пряма є також графіком лінійної функції). Отже, завдання уроку: познайомитися з таким видом рівнянь, які подаються в № 4, та вивчити їх особливості й властивості.
IV. Актуалізація опорних знань
Запитання до класу («Мікрофон» або ігровий момент «Найрозумніший»)
- Що називається розв'язком рівняння з двома змінними?
- Чи є пара чисел (4; 1) розв'язком рівняння х – 2у = 2?
- Що називається графіком рівняння з двома змінними? Чи завжди таке рівняння має графік?
- Які рівняння із двома змінними називаються рівносильними? Яку властивість мають графіки рівносильних рівнянь?
- Серед даних рівнянь із двома змінними виберіть пари таких, що мають однакові графіки, та поясність, чому ви так вважаєте:
1) х + у = 2; 2) у = х + 2; 3) у = ![]() ; 4) 2у = х; 5) у = -х + 2.
; 4) 2у = х; 5) у = -х + 2.
V. Вивчення нового матеріалу
Узагальнивши вид рівнянь із двома змінними, що подаються в № 4 домашнього завдання, формулюємо означення лінійного рівняння з двома змінними (звертаємо увагу на фразу «рівняння виду», що означає рівняння, яке можна записати в такому вигляді).
Після цього з'ясуємо вид графіка лінійного рівняння: якщо хоча б один з коефіцієнтів а або b рівняння ax + by + c = 0 не дорівнює 0, шляхом тотожних перетворень лінійне рівняння приводимо до вигляду y = kx + b і робимо висновок: графік лінійного рівняння збігається в цьому випадку із графіком лінійної функції, тобто є прямою. Розглядаючи приклади на побудову графіків лінійних рівнянь із двома змінними, звертаємо увагу учнів на те, що графік лінійного рівняння (якщо хоча б один із коефіцієнтів а або b не дорівнює 0) можна будувати за двома точками. Іноді за такі точки беруться точки перетину графіка з координатними осями (якщо ці точки не дуже віддалені від початку координат або, навпаки, не дуже близько розташовані від початку координат).
VI. Закріплення знань. Вироблення вмінь
Виконання усних вправ
- Серед поданих рівнянь назвіть лінійні рівняння з двома невідомими:
1) ху = 3; 2) х + 2у = 7; 3) х + у2 = 4; 4) х - у = 1; 5) 12х + 10у = 0;
6) 0х – 2у = 3; 7) 3х + 0у = 0; 8) 0х + 0у = 0; 9) 0х + 0у = 1.
- Назвіть кілька розв'язків лінійного рівняння 0,5х – у = 1.
- Як на координатній площині розташований графік рівняння:
1) х = -2; 2) у = 7; 3) 5 – х = 0; 4) 2х – 1 = 0?
Виконання письмових вправ:
-
Які з пар чисел (2; 2); (1; 3); (1; 3,5); (4; -1);
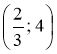 є розв'язками рівняння 3х + 2у = 10?
є розв'язками рівняння 3х + 2у = 10?
- Виразіть у через х у рівняннях та знайдіть два які-небудь розв'язки рівнянь:
1) х – у = 7; 2) 3х + 2у = 5.
- Які з точок К(2; 0,5); L(0; 2); M(2; 4); N(3; 0,25) не належать графіку рівняння -3х + 4у = 8?
- Побудуйте графік рівняння:
1) x – 3у = 6; 2) x – 2у = 0; 3) 1,5х = 6; 4) -0,3у = 0,6;
5) 5х – 6у = 4; 6) 8х + 16у = 24.
- На прямій, яка є графіком рівняння 4х + 9у = 1, узяли точку, ордината якої дорівнює 1. Знайдіть абсцису цієї точки.
- Знайдіть значення коефіцієнта а в рівнянні ах + 3у = 4, якщо відомо, що графік рівняння проходить через точку (1; 2). Побудуйте графік рівняння.
VII. Підсумки уроку
Контрольні запитання
- Яке рівняння з двома змінними називається лінійним? Наведіть приклад такого рівняння.
- Яка фігура є графіком лінійного рівняння ах + bу = с, в якому хоча один з коефіцієнтів а чи b не дорівнює сумі? Як розташований в координатній площині графік рівняння х = т; у = n?
VII. Домашнє завдання
№ 1. Вивчіть зміст нових понять уроку.
№ 2. Виразіть у через х у рівнянні та знайдіть два будь-які розв'язки рівняння:
1) 5х – 2у = 8; 2) 2х – 5у = 7; 3) 3х + 2у = 10.
№ 3. (Пара чисел) точка (є розв'язком рівняння) належить графіку рівняння 2х + bу = 12. Знайдіть b та побудуйте графік рівняння.
№ 4. В одній системі координат побудуйте графіки рівнянь:
1) х + у = 2; 2) –х – у = -2; 3) 2х + 7у = 4.
Чому графіками цих рівнянь є одна й та сама пряма?
№ 5. Повторіть означення модуля числа. Закінчіть запис:
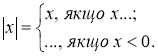


про публікацію авторської розробки
Додати розробку
